【概率论与数理统计】第三章 多维随机变量及其分布(3)

2 随机变量的独立性

2.1 两个随机变量的独立性

在多维随机变量中各分量的取值有时会互相影响，但有时也会毫无影响。

例如，一个人的身高\(X\)和体重\(Y\)之间就会互相影响，但与收入\(Z\)一般就没什么影响。

这里，我们根据两个事件的独立性引出两个随机变量的独立性：

之前我们这样描述：事件\(\{X \le x\}\)与事件\(\{Y \le y\}\)的积事件\(\{X \le x,\ Y \le y\}\)，若：\(P\{X \le x, Y \le y\} = P\{X \le x\} \cdot P\{Y \le y\}\)，则事件\(\{X \le x\}\)与事件\(\{Y \le y\}\)相互独立。

定义9：设二维随机变量\((X,Y)\)的分布函数为\(F(x,y)\)，边缘分布函数为\(F_X(x),\ F_Y(y)\)，若对任意\(x,y\)，有：

\(P\{X \le x, Y \le y\} = P\{X \le x\} \cdot P\{Y \le y\}\) 即：

\(F(x,y) = F_X(x) \cdot F_Y(y)\)

则称： 二维随机变量\((X,Y)\)的分量\(X\)与\(Y\)相互独立。

例1：设二维随机变量\((X,Y)\)的分布函数\(F(x,y)\)为：

\[F(x,y) = \begin{cases} (1-e^{-3x})(1-e^{-4y}),\ \ \ \ & x \gt 0,y \gt 0 \\ 0,\ &其他 \end{cases} \]

证明：\(X\)与\(Y\)相互独立。

证明：关于\(X\)的边缘分布函数为： # 分布函数的含义，本章定义2

\[F_X(x) = F(x, +\infty) = \begin{cases} 1-e^{-3x}, \ \ \ \ & x \gt 0 \\ 0,\ &其他 \end{cases} \]

同理，关于\(Y\)的边缘分布函数为：

\[F_Y(y) = F(+\infty, y) = \begin{cases} 1-e^{-4y}, \ \ \ \ & y \gt 0 \\ 0,\ &其他 \end{cases} \]

因此，对任意\(x,y\)，都有\(F(x,y) = F_X(x) \cdot F_Y(y)\)成立，故\(X,Y\)相互独立。

2.2 二维离散型随机变量的独立性

设\((X,Y)\)为二维离散型随机变量，其分布律为：\(p_{ij} = P\{X=x_i, Y = y_j\},\ \ i,j = 1,2,...\)；边缘分布律为：

\(p_{i\cdot} = P\{X = x_i\} = \sum_{j=1}^{\infty} p_{ij},\ \ j = 1,2,...\)；

\(p_{\cdot j} = P\{Y = y_j\} = \sum_{i=1}^{\infty} p_{ij},\ \ i = 1,2,...\)；

若对于\((X,Y)\)的所有取值\(x_i,y_j\)，都有：

\(p_{ij} = P\{X=x_i, Y = y_j\} = P\{X = x_i\} \cdot P\{Y = y_j\},\ \ i,j = 1,2,...\)

则称\((X,Y)\)为二维离散型随机变量的分量\(X\)与\(Y\)相互独立。

例2：盒中有2个红球和3个白球，从中每次任取一个球；连续取两次，记事件\(X、Y\)分别表示第一、二次是否取到红球，"1"表示取到红球，"0"表示取到白球；分别进行有放回取球和无放回取球，分别求出两种情形下\((X,Y)\)的\(X\)与\(Y\)是否相互独立。

解：该题的题干是本章3.1中例6的内容；要求二维随机变量\((X,Y)\)各分量是否相互独立，需要先获取\((X,Y)\)的分布律；前面的例6中已经求得，我们直接拿来用：

（1）有放回地取球情形：

\((X,Y)\)的分布律与边缘分布律为：

X	Y	Y	\(p_{i\cdot}\)
X	0	1	\(p_{i\cdot}\)
0	\(\frac{9}{25}\)	\(\frac{6}{25}\)	\(\frac{3}{5}\)
1	\(\frac{6}{25}\)	\(\frac{4}{25}\)	\(\frac{2}{5}\)
\(p_{\cdot j}\)	\(\frac{3}{5}\)	\(\frac{2}{5}\)	1

因为：\(P\{X=0,Y=0\} = \frac{9}{25} = P\{X=0\} \cdot P\{Y=0\} = p_{i\cdot} \cdot p_{\cdot j} = \frac{3}{5} \cp \frac{3}{5}\)

\(P\{X=0,Y=1\} = \frac{6}{25} = P\{X=0\} \cdot P\{Y=1\} = p_{i\cdot} \cdot p_{\cdot j} = \frac{3}{5} \cp \frac{2}{5}\)

\(P\{X=1,Y=0\} = \frac{6}{25} = P\{X=1\} \cdot P\{Y=0\} = p_{i\cdot} \cdot p_{\cdot j} = \frac{2}{5} \cp \frac{3}{5}\)

\(P\{X=1,Y=1\} = \frac{4}{25} = P\{X=1\} \cdot P\{Y=1\} = p_{i\cdot} \cdot p_{\cdot j} = \frac{2}{5} \cp \frac{2}{5}\)

可见，对于任意的\(x,y\)都有\(P\{X=x_i, Y = y_j\} = P\{X = x_i\} \cdot P\{Y = y_j\}\)；因此，\(X\)与\(Y\)相互独立。

（2）无放回地取球情形：

\((X,Y)\)的分布律与边缘分布律为：

X	Y	Y	\(p_{i\cdot}\)
X	0	1	\(p_{i\cdot}\)
0	\(\frac{3}{10}\)	\(\frac{3}{10}\)	\(\frac{3}{5}\)
1	\(\frac{3}{10}\)	\(\frac{1}{10}\)	\(\frac{2}{5}\)
\(p_{\cdot j}\)	\(\frac{3}{5}\)	\(\frac{2}{5}\)	1

由于\(P\{X=0,Y=0\} = \frac{3}{10}\)；而\(P\{X=0\} \cdot P\{Y=0\} = p_{i\cdot} \cdot p_{j \cdot} = \frac{3}{5} \cp \frac{3}{5} = \frac{9}{25}\)；可见两者并不相等，因此\(X\)与\(Y\)不是相互独立的。

例3：设二维随机变量\((X,Y)\)的分布律为：

X	Y	Y
X	1	2
1	\(\frac{1}{9}\)	a
2	\(\frac{1}{6}\)	\(\frac{1}{3}\)
3	\(\frac{1}{18}\)	b

且\(X\)与\(Y\)相互独立，其常数\(a,b\)。

解：由于\(X\)与\(Y\)相互独立，所以：

\(P\{X=1,Y=1\} =\frac{1}{9} = P\{X=1\} \cdot P\{Y=1\} = (\frac{1}{9} + a)(\frac{1}{9} + \frac{1}{6})\) 得：\(a = \frac{2}{9}\)

\(b\)的解法有两种：

①利用全分布律之和等于1：\(\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} p_{ij} = 1\) 解得\(b = \frac{1}{9}\)

②利用与解a方法类似的办法：例如：\(P\{X=3,Y=1\} = \frac{1}{18} = P\{X=3\} \cdot P\{Y=1\} = (\frac{1}{18} + b)(\frac{1}{9} + \frac{1}{6} + \frac{1}{18})\) 解得\(b = \frac{1}{9}\)

2.3 二维连续型随机变量的独立性

二维连续型随机变量\((X,Y)\)的概率密度为\(f(x,y)\)，关于\(X\)与关于\(Y\)的边缘概率密度为\(f_X(x)\)和\(f_Y(y)\)，若对于\((X,Y)\)所有取值\((x,y)\)都有：\(f(x,y) = f_X(x) \cdot f_Y(y)\)成立，则称随机变量\(X\)与\(Y\)是相互独立的。

例4：二维随机变量\((X,Y)\)的分布函数为：\(F(x,y) = a(b + \arctan{x})(c + \arctan{y}),\ \ -\infty \lt x,y \lt +\infty\) ；证明随机变量\(X\)与\(Y\)相互独立。

证明：本例的题干部分是本章节3.1中例8的题干，因此利用在例8中解得的：

\(a = \frac{1}{\pi^2},\ \ b = \frac{\pi}{2},\ \ c = \frac{\pi}{2}\)

概率密度为：\(f(x,y) = \frac{1}{\pi^2} \cdot \frac{1}{1+x^2} \cdot \frac{1}{1+y^2} = \frac{1}{\pi^2(1+x^2)(1+y^2)},\ \ -\infty \lt x,y \lt +\infty\)

继续解得关于\(X\)的边缘密度为：

\[\begin{align} f_X(x) = \int_{-\infty}^{+\infty} f(x,y) dy &= \int_{-\infty}^{+\infty} \frac{1}{\pi^2(1+x^2)(1+y^2)} dy \\ &= \frac{1}{\pi^2 (1+x^2)} \arctan{y} |_{-\infty}^{+\infty}\\ &= \frac{1}{\pi (1+x^2)},\ \ \ \ -\infty \lt x \lt +\infty \end{align} \]

同理关于\(Y\)的边缘密度为：

\[\begin{align} f_Y(y) = \int_{-\infty}^{+\infty} f(x,y) dx &= \int_{-\infty}^{+\infty} \frac{1}{\pi^2(1+x^2)(1+y^2)} dx \\ &= \frac{1}{\pi^2 (1+y^2)} \arctan{x} |_{-\infty}^{+\infty}\\ &= \frac{1}{\pi (1+y^2)},\ \ \ \ -\infty \lt y \lt +\infty \end{align} \]

可见对于任意的\((x,y)\)都有：\(f(x,y) = f_X(x) \cdot f_Y(y)\)；因此，随机变量\(X\)与\(Y\)相互独立。

例5：设随机变量\((X,Y) \sim N(\mu_1,\mu_2,\sigma_1,\sigma_2,\rho)\)，试求\(X\)与\(Y\)相互独立的充分必要条件。

解：已知\(f(x,y) = \frac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} e^{-\frac{1}{2(1-\rho^2)} [\frac{(x-\mu_1)^2}{\sigma_1^2} -2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1 \sigma_2} + \frac{(y-\mu_2)^2}{\sigma_2^2}]}\)

我们指代服从正态分布的二维随机变量\((X,Y)\)，其分量也各自服从正态分布，即：

\(X \sim N(\mu_1,\sigma_1),\ \ Y \sim N(\mu_2, \sigma_2)\)

也就是：

\(f_X(x) = \frac{1}{\sqrt{2\pi} \sigma_1} e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2}},\ \ \ \ -\infty \lt x \lt +\infty\)

\(f_Y(y) = \frac{1}{\sqrt{2\pi} \sigma_2} e^{-\frac{(y-\mu_2)^2}{2\sigma_2^2}},\ \ \ \ -\infty \lt y \lt +\infty\)

从而：

（1）若\(\rho = 0\)，则：

\(f(x,y) = \frac{1}{2\pi \sigma_1 \sigma_2 } e^{-\frac{1}{2} [\frac{(x-\mu_1)^2}{\sigma_1^2} + \frac{(y-\mu_2)^2}{\sigma_2^2}]} = f_X(x) \cdot f_Y(y)\)

表明\(X\)与\(Y\)相互独立。

（2）若\(X\)与\(Y\)相互独立，则对于所有的\((x,y)\)都有：

\(f(x,y) = f_X(x) \cdot f_Y(y)\) ；特别地，令\(x=\mu_1,\ y = \mu_2\)，有：

\(f(x,y) = \frac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}} e^0 = \frac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1-\rho^2}}\)

\(f_X(x) \cdot f_Y(y) = \frac{1}{\sqrt{2\pi} \sigma_1} e^0 \cdot \frac{1}{\sqrt{2\pi} \sigma_2} e^0 = \frac{1}{2\pi \sigma _1 \sigma_2}\)

因此，\(\sqrt{1-\rho^2} = 1\)，即\(\rho = 0\)。

综上所述：\(X\)与\(Y\)相互独立的充要条件是\(\rho = 0\)。

例6：设二维随机变量\((X,Y)\)在一原点为圆心，半径为1的圆形区域上服从均匀分布，问\(X\)与\(Y\)是否相互独立？

解：由题知\((X,Y)\)的概率密度为：

\[f(x,y) = \begin{cases} \frac{1}{\pi},\ \ \ \ &x^2 + y^2 \le 1 \\ 0, &其他 \end{cases} \]

\((X,Y)\)关于\(X\)的边缘密度为：

\[\begin{align} f_X(x) &= \begin{cases} \int_{-\infty}^{+\infty} f(x,y) dy, \ \ \ \ &-1 \le x \le 1 \\ 0, &其他 \end{cases} \\ \\ &= \begin{cases} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \frac{1}{\pi} dy, \ \ \ \ &-1 \le x \le 1 \\ 0, &其他 \end{cases} \\ \\ &= \begin{cases} \frac{2}{\pi} \sqrt{1-x^2} , \ \ \ \ &-1 \le x \le 1 \\ 0, &其他 \end{cases} \end{align} \]

同理，\((X,Y)\)关于\(Y\)的边缘密度为：

\[\begin{align} f_Y(y) &= \begin{cases} \int_{-\infty}^{+\infty} f(x,y) dx, \ \ \ \ &-1 \le y \le 1 \\ 0, &其他 \end{cases} \\ \\ &= \begin{cases} \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} \frac{1}{\pi} dx, \ \ \ \ &-1 \le y \le 1 \\ 0, &其他 \end{cases} \\ \\ &= \begin{cases} \frac{2}{\pi} \sqrt{1-y^2} , \ \ \ \ &-1 \le y \le 1 \\ 0, &其他 \end{cases} \end{align} \]

因此：

\[f_X(x) \cdot f_Y(y) = \begin{cases} \frac{4}{\pi} \sqrt{1-x^2} \sqrt{1-y^2}, \ \ \ \ & |x| \le 1,|y| \le 1 \\ 0, &其他 \end{cases} \]

易见当\(|x| \le 1,\ |y| \le 1\)时，\(f(x,y) \ne f_X(x) \cdot f_Y(y)\)；所以，\(X\)与\(Y\)不是相互独立的。

经过以上的讨论，我们可以发现，联合分布可以i确定边缘分布，但一般来说，边缘分布不能确定联合分布。但是当\(X\)与\(Y\)相互独立的情况下\((X,Y)\)的分布可以由它的两个边缘分布确定。

例7：设\(X\)与\(Y\)是相互独立的随机变量，\(X\)在\([-1,1]\)上服从均匀分布，\(Y\)服从指数分布，其概率密度为：

\[f_Y(y) = \begin{cases} 2e^{-2y},\ \ \ \ & y \gt 0 \\ 0, &其他 \end{cases} \]

求\((X,Y)\)的概率密度。

解：由已知得\(X\)的概率密度为：

\[f_X(x) = \begin{cases} \frac{1}{2},\ \ \ \ & -1 \le x \le 1 \\ 0，其他 \end{cases} \]

因为\(X\)与\(Y\)hi相互独立的，所以\((X,Y)\)的概率密度为：

\[f(x,y) = f_X(x) \cdot f_Y(y) = \begin{cases} e^{-2y},\ \ \ \ & -1\ le x \le 1, y \gt 0 \\ 0, &其他 \end{cases} \]

例8：设二维随机变量\((X,Y)\)的概率密度为：

\[f(x,y) = \begin{cases} 8xy, \ \ \ \ & 0 \le x \le 1, 0 \le y \le x \\ 0, & 其他 \end{cases} \]

求关于\(X\)与\(Y\)的边缘概率密度，并判断\(X\)与\(Y\)是否相互独立。

解：首先画图：

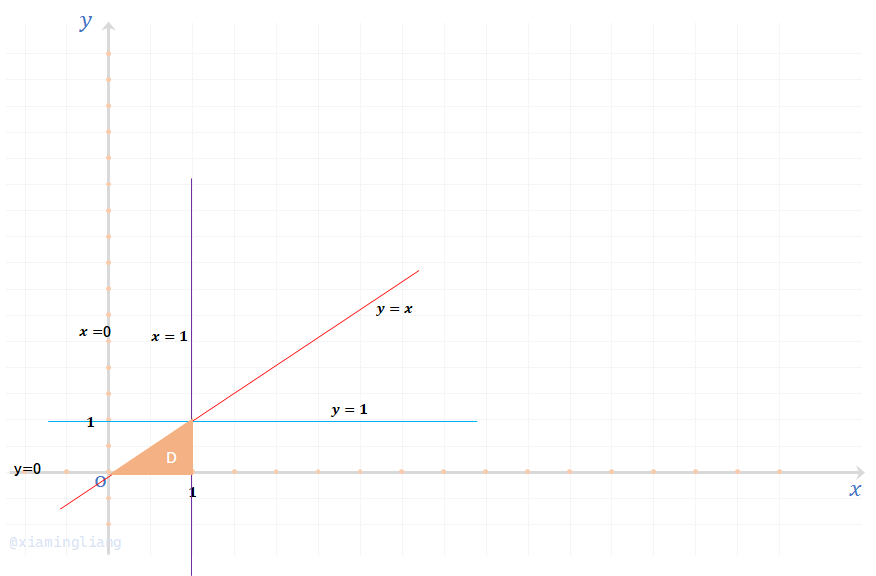
然后由\((X,Y)\)的密度函数的其关于\(X\)的边缘密度为：(y的取值是从0到x的)

\[\begin{align} f_{X}(x) = \int_{-\infty}^{+\infty} f(x,y)dy &= \begin{cases} \int_{0}^{x} 8xy dy,\ \ \ \ &0 \le x \le 1 \\ 0, & 其他\\ \end{cases} \\ &= \begin{cases} 4xy^2 |_{0}^{x},\ \ \ \ &0 \le x \le 1 \\ 0, & 其他\\ \end{cases} \\ &= \begin{cases} 4x^3 ,\ \ \ \ &0 \le x \le 1 \\ 0, & 其他\\ \end{cases} \end{align} \]

同理得\((X,Y)\)关于X的边缘密度为：

\[\begin{align} f_{Y}(y) = \int_{-\infty}^{+\infty} f(x,y)dx &= \begin{cases} \int_{y}^{1} 8xy dx,\ \ \ \ &0 \le y \le 1 \\ 0, & 其他\\ \end{cases} \\ &= \begin{cases} 4y(1-y^2) ,\ \ \ \ &0 \le y \le 1 \\ 0, & 其他\\ \end{cases} \end{align} \]

当\(0 \le x \le 1,\ 0\le y \le x\)时\(f(x,y) \ne f_X(x) \cdot f_Y(y)\)，所以，\(X\)与\(Y\)不是相互独立的。

在实际应用中，往往不采用数学定义来判定事件是否独立，而是直接按照实际意义来考证。

2.4 \(n\)个随机变量的相互独立

将前文中两个随机变量相互独立的概念推广到\(n\)个。

定义10：设\(n\)维连续型随机变量\((X_1,\ X_2,\ ...,\ X_n)\)的分布函数为\(F(x_1,x_2,...,x_n) = P\{X1\le x_1,\ X_2 \le x_2, ...,\ X_n \le x_n\}\)，该列车密度为\(f(x_1,x_2,...,x_n)\)，则\((X_1,\ X_2,\ ...,\ X_n)\)关于\(X_k,\ k=1,2,...,n\)的边缘分布函数和边缘概率密度分别为：

\(F_{X_k}(x_k) = P\{X_1 \lt +\infty,\ X_2 \lt +\infty,\ ...,\ X_k \le x_k,\ ...,\ X_n \lt +\infty,\}\)

\(f_{X}(x_k) = \underbrace{\int_{-\infty}^{+\infty} ... \int_{-\infty}^{+\infty}}_{n-1个} f(x_1,...,x_{k-1},x_k,x_{k+1},...,x_n)dx_1 ... dx_{k-1} dx_{k} dx_{k+1} ... dx_n\)

定义11：若对一切的\(x_1,x_2,...,x_n\)有：

\(P\{X_1\le x_1,X_2 \le x_2,...,X_n \le x_n\} = \Pi_{k=1}^{n} P\{X_k \le x_k\}\)，即：

\(F(x_1,x_2,...,x_n) = F_{X_1}(x_1) \cdot F_{X_2}(x_2) \cdot ... \cdot F_{X_n}(x_n)\)则称：这\(n\)个随机变量间时相互独立的。

例9：设\(X_1,\ X_2,\ ...,\ X_n\) 相互独立，且\(X_i \sim N(\mu, \sigma^2),\ i=1,2,...,n\)；求\((X_1,\ X_2,\ ...,\ X_n)\)的概率密度。

解：由于\(X_i \sim N(\mu, \sigma^2),\ i=1,2,...,n\)，故：

\(f_{X_k}(x_k) = \frac{1}{\sqrt{2\pi} \sigma} e^{- \frac{(x_k - \mu)^2}{2\sigma^2}},\ \ -\infty \lt x_k \lt +\infty\) ；又因为\(X_1,\ X_2,\ ...,\ X_n\) 相互独立，所以：

\(f(x_1,x_2,...,x_n) = f_{X_1}(x_1) \cdot f_{X_2}(x_2) \cdot ... \cdot f_{X_n}(x_n) = \frac{1}{(2\pi)^\frac{n}{2} \sigma_1 \sigma_2...\sigma_n} e^{ -\frac{1}{2} [\frac{(x_1 -\mu)^2}{\sigma_1^2} + \frac{(x_2 -\mu)^2}{\sigma_2^2} + ... + \frac{(x_n -\mu)^2}{\sigma_n^2}] }\)

还可以证明：

(1) 其中任意\(k\)个\((2 \le k \le n)\)随机变量也相互独立

(2) 他们各自的函数\(g_1(X_1),g_2(X_2),...,g_n(X_n)\)也相互独立，比如：\(X_1^2, x_2^2,...,X_n^2\)相互独立。

例10：设随机变量\(X\)与\(Y\)相互独立，都服从区间\([1,3]\)上的均匀分布，设\(1 \lt a \lt 3\)，若事件\(A = \{X \le a\},\ B= \{Y \gt a\}\)，且\(P(A \cup B) = \frac{7}{9}\)，求常数\(a\)的值。

解：由已知得\(X、Y\)的概率密分别为：

\[f_X(x) = \begin{cases} \frac{1}{2},\ \ \ \ &1 \le x \le 3 \\ 0,\ &其他 \end{cases} \ \ \ \ \ \ \ \ \ \ , \ \ \ \ \ \ \ \ \ \ f_Y(y) = \begin{cases} \frac{1}{2},\ \ \ \ &1 \le y \le 3 \\ 0,\ &其他 \end{cases} \]

因此，当\(1 \lt a \lt 3\)时，事件\(A、B\)的概率分别为：

\(P(A) = P\{X \le a\} = F_X(a) = \int_{-\infty}^{a} f_X(x) dx =\int_{1}^{a} f_X(x) dx = \frac{1}{2}x |_1^a = \frac{a-1}{2}\)

\(P(B) = P\{Y \gt a\} = \int_{a}^{+\infty} f_Y(y) dy = \int_{a}^{3} f_Y(y)dy = \frac{1}{2}y | _{a}^{3} = \frac{3-a}{2}\)

由\(X\)与\(Y\)相互独立可知：

\(P(AB) = P(A) P(B) = \frac{(a-1)(3-a)}{4}\)

而\(P(A \cup B) = P(A) + P(B) - P(AB) = \frac{7}{9}\)得：

\(\frac{a-1}{2} + \frac{3-a}{2} - \frac{(a-1)(3-a)}{4} = \frac{7}{9}\) 得：\(a = \frac{5}{3}或 \frac{7}{3}\)