【概率论与数理统计】第三章 多维随机变量及其分布(1)
1 多维随机变量的概念
1.1 二维随机变量及其分布函数
在实际问题中,通常需要多个随机变量才能较好地描述某一随机现象;例如,打靶时,弹着点是由两个随机变量所构成的(横、纵坐标);飞机重心在空中的位置是由三个随机变量(三位坐标)来确定的;学生的考试成绩是由多个随机变量(每门课程的成绩)组成的。
为了研究这些随机现象的规律性,引入了多为随机变量的概念。
定义1:由\(n\)个随机变量\(X_1,\ X_2,\ ...,\ X_n\)构成的整体\(X = (X_1,\ X_2,\ ...,\ X_n)\),称为\(n\)维随机变量;\(X_k\ (k =1,2,...,n )\)称为\(X\)的第\(k\)个分量</u>。
特别地,当\(n=1\)时,\(X\)称为一维随机变量;当\(n=2\)时,\(X\)称为二维随机变量。
从几何角度看,一维随机变量是直线上的随机点,二维随机变量是平面上的随机点。
定义2:设\((X,Y)\)是二维随机变量,对任意的实数\(x,y\),二元函数\(F(x,y) = P\{X \le x,\ Y \le y\},\ \ -\infty \lt x,y \lt +\infty\);称为\(X,Y\)的联合分布函数或者二维随机变量\((X,Y)\)的分布函数。
\(X\)与\(Y\)各自的分布函数分别称为\((X,Y)\)关于\(X\)与关于\(Y\)的边缘分布函数,分别记作\(F_X(x)\)与\(F_Y(y)\);则:
\(F_X(x) = P\{X \le x\} = P\{X \le x, Y \lt +\infty\} = F(x, +\infty) = \lim_{y \to +\infty} F(x,y)\) ;
\(F_Y(y) = P\{Y \le y\} = P\{X \lt +\infty, Y \le y\} = F(+\infty, y) = \lim_{x \to +\infty} F(x,y)\)。
在几何上,若将二维随机变量\((X,Y)\)看作是平面上随机点的坐标,那么,点\((x,y)\)处的分布函数值\(F(x,y)\)就是随机点\((x,y)\)落在以点\((x,y)\)为顶点而位于该点左下方的无穷矩形区域内的概率。 如图:
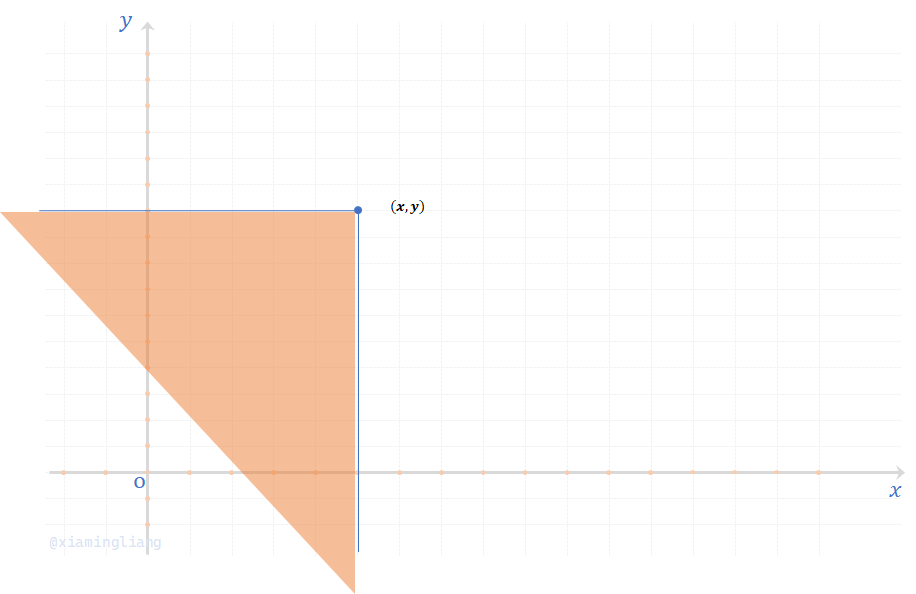
随机点落在区域\(\{x_1 \lt X \le x_2,\ y_1 \lt Y \le y_2\}\)的概率为:\(P\{x_1 \lt X \le x_2,\ y_1 \lt Y \le y_2\} = F(x_2,y_2) - F(x_2,y_1) - F(x_1, y_2) + F(x_1, y_1)\)。
二维随机变量的分布函数\(F(x,y)\)具有以下性质:
(1) [单调性]: \(F(x,y)\)分别对\(x\)和对\(y\)是单调不减的,即:
当\(x_1 \lt x_2\)时,有\(F(x_1, y) \le F(x_2, y)\);
当\(y_1 \lt y_2\)时,有\(F(x,y_1) \le F(x,y_2)\)。
(2) [有界性]:对任意的\(x\)和\(y\),有:\(0 \le F(x,y) \le 1\)且
\(F(-\infty,y) = \lim_{x \to -\infty} F(x,y) = 0\)
\(F(x, -\infty) = \lim_{y \to -\infty} F(x,y) = 0\)
\(F(-\infty, -\infty) = \lim_{x,y \to -\infty} F(x,y) = 0\)
\(F(+\infty,+\infty) = \lim_{x,y \to +\infty} F(x,y) = 1\)
(3) [右连续性]: 对每个变量都是右连续的,即:
\(F(x+0,y) = F(x,y)\)
\(F(x,y+0) = F(x,y)\)
(4) [非负性]: 对任意的\(x_1 \lt x_2, y_1 \lt y_2\)有:
\(P\{x_1 \lt X \le x_2,\ y_1 \lt Y \le y_2\} = F(x_2,y_2) - F(x_2,y_1) - F(x_1, y_2) + F(x_1, y_1) \ge 0\)
具有上述四条性质的二元函数\(F(x,y)\)一定是某个二维随机变量的分布函数;反之,任意一个二维随机变量的分布函数\(F(x,y)\)必定具备上述性质。
注意:性质4是二维随机变量特有的,一维随机变量没有。
例1:判断二元函数
是否是某个二维随机变量的分布函数。
解:性质1:单调性:\(G'(x,y) = 0\);证明其单调不减。
性质2:有界性:\(G(x,y)\)的取值只有0和1,满足\(0\le G(x,y) \le 1\);因此有界。
性质3:满足有连续性 # 应该是不连续才对啊,书本上应该是错了。
性质4:非负性:取\(a=c=-1,\ \ b=d=1\),则\(P\{a \lt X \le b,\ c \lt y \le d\} = F(b,d) - F(b,c) - F(a,d) - F(a,c) = 1 - 1 - 1 + 0 = -1\);因此不满足非负性。
综上,它不是某个二维随机变量的分布函数。
1.2 二维离散型随机变量的分布律和边缘分布律
定义3:若随机变量\((X,Y)\)的取值只是有限对或者可列的无限多对,则称\((X,Y)\)为二维离散型随机变量。
设二维离散型随机变量\((X,Y)\)的所有可能取的值为\((x_i, y_j),\ \ i,j = 1,2,...\);其相应的概率为:\(P\{X=x_i,\ Y=y_j\} = p_{ij}\);则称\(p_{ij}\)为二维离散型随机变量\((X,Y)\)的分布律或\(X\)与\(Y\)的联合分布律。
\((X,Y)\)的分布律也可以用表格形式表达:
| X | Y | Y | Y | Y | Y |
|---|---|---|---|---|---|
| X | \(y_1\) | \(y_2\) | ... | \(y_i\) | ... |
| \(x_1\) | \(p_{11}\) | \(p_{12}\) | ... | \(p_{1j}\) | ... |
| \(x_2\) | \(p_{21}\) | \(p_{22}\) | ... | \(p_{2j}\) | ... |
| ... | .... | ... | ... | ... | ... |
| \(x_i\) | \(p_{i1}\) | \(p_{i2}\) | ... | \(p_{ij}\) | ... |
| ... | ... | ... | ... | ... | ... |
显然,二维离散型随机变量\((X,Y)\)的分布律具有如下两条基本性质:
(1) 非负性:\(p_{ij} \ge 0,\ \ i,j = 1,2,...\) ;
(2) 规范性:\(\sum_{i=1}^{\infty} \sum_{j=1}^{\infty} p_{ij} = 1\) 。
例2:设二维随机变量\((X,Y)\)的分布律为:
| X | Y | Y | Y |
|---|---|---|---|
| X | 1 | 2 | 3 |
| 1 | \(\frac{1}{3}\) | \(\frac{a}{6}\) | \(\frac{1}{4}\) |
| 2 | 0 | \(\frac{1}{4}\) | \(a^2\) |
求\(a\)的值。
解:由分布律的性质知:\(\frac{1}{3} + \frac{a}{6} + \frac{1}{4} + 0 + \frac{1}{4} + a^2 = 1\)
即:\(6a^2 + a -1 = (2a + 1)(3a - 1) = 0\ \ \ \ \ \ \therefore a = -\frac{1}{2},\ \ \ a = \frac{1}{3}\)
由于分布律的非负性得:\(a = \frac{1}{3}\)
例3:设二维随机变量\((X,Y)\)得分布律为:
| X | Y | Y | Y |
|---|---|---|---|
| X | 1 | 2 | 3 |
| 0 | 0.1 | 0.1 | 0.3 |
| 1 | 0.25 | 0 | 0.25 |
求:(1)\(P\{X = 0\}\); (2)\(P\{Y \le 2\}\); (3)\(P\{X \lt 1,\ Y \le 2\}\); (4)\(P\{X+Y = 2\}\);
解:(1)\(\{X = 0\} = \{X=0,Y=1\} \cup \{X=0,Y=3\} \cup \{X=0,Y=3\}\),且他们之间互不相容,所以:\(P\{X=0\} = 0.1 + 0.1 + 0.3 = 0.5\)
(2)\(\{Y \le 2\} = \{Y = 1\} + \{Y = 2\} = \{X=0,Y=1\} \cup \{X=1,Y=1\} \cup \{X=0,Y=2\} \cup \{X=1,Y=2\}\) ,且他们之间互不相容,所以:\(P\{Y \le 2\} = 0.1 + 0.25 + 0.1 + 0 = 0.45\)
(3)\(\{X \lt 1, Y\le 2\} = \{X=0, Y=1\} \cup \{X=0, Y=2\}\) ,且他们之间互不相容,所以:\(\{X \lt 1, Y\le 2\} = 0.1 + 0.1 = 0.2\)
(4)\(P\{X+Y = 2\} = P\{X=0,Y=2\} \cup \{X=1,Y=1\}\) ,且他们之间互不相容,所以:\(P\{X+Y = 2\} = 0.1 + 0.25 = 0.35\)
例4:现有3个整数\(1,2,3\),\(X\)表示从这3个数中随机抽取1个整数,\(Y\)表示从\(1\)到\(X\)中随机抽取1个整数,试求\((X,Y)\)的分布律。
解:\(X\)与\(Y\)可能的取值均为\(1,2,3\),利用概率乘法公式,可得\((X,Y)\)取各对数值的概率分别是:
\(P\{X=1,Y=1\} = P\{X=1\} \cdot P\{Y=1\} = \frac{1}{3} \cdot 1 = \frac{1}{3}\)
\(P\{X=2,Y=1\} = P\{X=2\} \cdot P\{Y=1\} = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}\)
\(P\{X=2,Y=2\} = P\{X=2\} \cdot P\{Y=2\} = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}\)
\(P\{X=3,Y=1\} = P\{X=3\} \cdot P\{Y=1\} = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}\)
\(P\{X=3,Y=2\} = P\{X=3\} \cdot P\{Y=2\} = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}\)
\(P\{X=3,Y=3\} = P\{X=3\} \cdot P\{Y=3\} = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}\)
另外,\(\{X=1,Y=2\},\ \{X=1,Y=3\},\ \{X=2,Y=3\}\)为不可能事件,概率均为0,从而\((X,Y)\)的分布律为:
| X | Y | Y | Y |
|---|---|---|---|
| X | 1 | 2 | 3 |
| 1 | \(\frac{1}{3}\) | 0 | 0 |
| 2 | \(\frac{1}{6}\) | \(\frac{1}{6}\) | 0 |
| 3 | \(\frac{1}{9}\) | \(\frac{1}{9}\) | \(\frac{1}{9}\) |
定义4:对于二维离散型随机变量\((X,Y)\),其分量\(X\)与\(Y\)各自的分布律分别称为\((X,Y)\)关于\(X\)与关于\(Y\)的边缘分布律,记作:
\(p_{i\cdot},\ i=1,2,...\)与\(p_{\cdot j},\ j=1,2,...\) 。
已知二维离散型随机变量\((X,Y)\)的分布律为:\(p_{ij} = P\{X=x_i,Y = y_j\},\ \ i,j = 1,2,...\) ,则\((X,Y)\)关于\(X\)的边缘分布律为:
\(p_{i\cdot} = P\{X=x_i\} = \sum_{j=1}^{\infty} P\{X=x_i,Y=Y_j\} = \sum_{j=1}^{\infty} p_{ij} ,\ \ i=1,2,...\);
同理,\((X,Y)\)关于\(Y\)的边缘分布律为:
\(p_{\cdot j} = P\{Y=y_j\} = \sum_{i=1}^{\infty} P\{X=x_i,Y=Y_j\} = \sum_{i=1}^{\infty} p_{ij} ,\ \ j=1,2,...\);
\((X,Y)\)的边缘分布律明显地具有以下性质:
\(p_{i\cdot} \ge 0,\ \ p_{\cdot j} \ge 0 ;\ \ \ \ i,j=1,2,...\) ; # 概率值肯定是正数,其实还得\(\le 1\)
\(\sum_{i=1}^{\infty} p_{i\cdot} = \sum_{j=1}^{\infty} p_{\cdot j} = 1\)。 # 实际上就是整个分布律表相加,这就包含了全部取值可能,结果肯定是1
例5:现有3个整数\(1,2,3\),\(X\)表示从这3个数中随机抽取1个整数,\(Y\)表示从\(1\)到\(X\)中随机抽取1个整数。(同例4)求\((X,Y)\)的边缘分布律。
解:首先,利用例4解得的\((X,Y)\)的分布律:
| X | Y | Y | Y |
|---|---|---|---|
| X | 1 | 2 | 3 |
| 1 | \(\frac{1}{3}\) | 0 | 0 |
| 2 | \(\frac{1}{6}\) | \(\frac{1}{6}\) | 0 |
| 3 | \(\frac{1}{9}\) | \(\frac{1}{9}\) | \(\frac{1}{9}\) |
然后,分别计算关于\(X\)和\(Y\)的边缘分布律;
关于\(X\)的边缘分布律:
\(P\{X=1\} = P\{X=1,Y=1\} + P\{X=1,Y=2\} + P\{X=1,Y=3\} = p_{1\cdot} = \frac{1}{3} + 0 + 0 = \frac{1}{3}\)
\(P\{X=2\} = P\{X=2,Y=1\} + P\{X=2,Y=2\} + P\{X=2,Y=3\} = p_{2\cdot} = \frac{1}{6} + \frac{1}{6} + 0 = \frac{1}{3}\)
\(P\{X=3\} = P\{X=3,Y=1\} + P\{X=3,Y=2\} + P\{X=3,Y=3\} = p_{3\cdot} = \frac{1}{9} + \frac{1}{9} + \frac{1}{9} = \frac{1}{3}\)
关于\(Y\)的边缘分布律:
\(P\{Y=1\} = P\{X=1,Y=1\} + P\{X=2,Y=1\} + P\{X=3,Y=1\} = p_{\cdot 1} = \frac{1}{3} + \frac{1}{6} + \frac{1}{9} = \frac{11}{18}\)
\(P\{Y=2\} = P\{X=1,Y=2\} + P\{X=2,Y=2\} + P\{X=3,Y=2\} = p_{\cdot 2} = 0 + \frac{1}{6} + \frac{1}{9} = \frac{5}{18}\)
\(P\{Y=3\} = P\{X=1,Y=3\} + P\{X=2,Y=3\} + P\{X=3,Y=3\} = p_{\cdot 3} = 0 + 0 + \frac{1}{9} = \frac{1}{9}\)
可将\((X,Y)\)的分布律即边缘分布律写在同一张表中:
| X | Y | Y | Y | \(p_{i\cdot}\) |
|---|---|---|---|---|
| X | 1 | 2 | 3 | \(p_{i\cdot}\) |
| 1 | \(\frac{1}{3}\) | 0 | 0 | \(\frac{1}{3}\) |
| 2 | \(\frac{1}{6}\) | \(\frac{1}{6}\) | 0 | \(\frac{1}{3}\) |
| 3 | \(\frac{1}{9}\) | \(\frac{1}{9}\) | \(\frac{1}{9}\) | \(\frac{1}{3}\) |
| \(p_{\cdot j}\) | \(\frac{11}{18}\) | \(\frac{5}{18}\) | \(\frac{1}{9}\) | 1 |
汇总下表格各区域的含义:
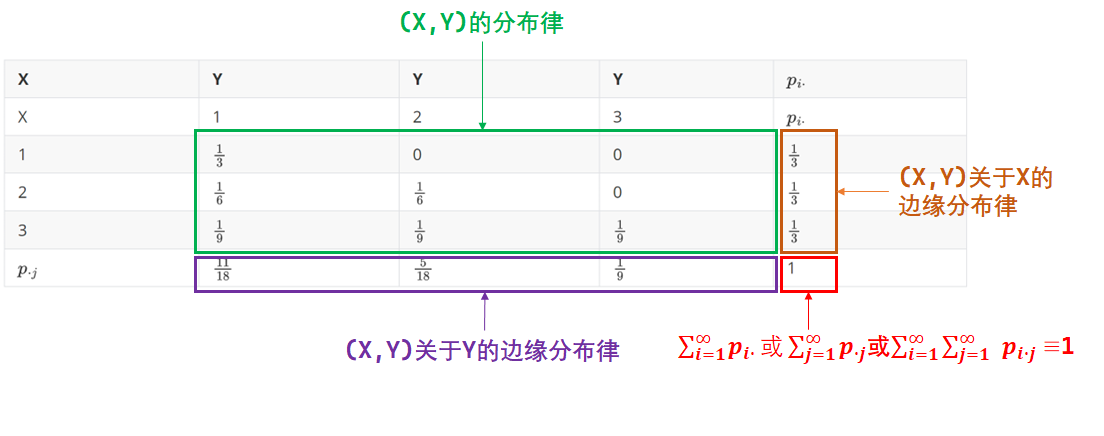
值得注意的是:
对于二维离散型随机变量\((X,Y)\)虽然他们的分布律可以确定他们的边缘分布律,但是一般情况下,边缘分布律是不能确定其分布律的。
例6:盒中有2个红球和3个白球,从中每次任取一个球;连续取两次,记事件\(X、Y\)分别表示第一、二次是否取到红球,"1"表示取到红球,"0"表示取到白球;分别进行有放回取球和无放回取球,分别求出两种情形下\((X,Y)\)的分布律与边缘分布律。
解:(1)有放回地取球情形
记事件\(\{X=1\}\)表示第一次取球取到的是红球,\(\{X=0\}\)表示第一次取球取到的是白球,则\(X\)的分布律为:
\(P\{X=1\} = \frac{2}{5},\ \ P\{X=0\} = \frac{3}{5}\);
同理,记事件\(\{Y=1\}\)表示第二次取球取到的是红球,\(\{Y=0\}\)表示第二次取球取到的是白球,则\(Y\)的分布律为:
\(P\{Y=1\} = \frac{2}{5},\ \ P\{Y=0\} = \frac{3}{5}\);
因执行的是有放回地取球,因此随机事件\(X\)与\(Y\)相互独立,所以:
\(P\{X=0,Y=0\} = P\{X=0\} \cdot P\{Y=0\} = \frac{3}{5} \cdot \frac{3}{5} = \frac{9}{25}\)
\(P\{X=0,Y=1\} = P\{X=0\} \cdot P\{Y=1\} = \frac{3}{5} \cdot \frac{2}{5} = \frac{6}{25}\)
\(P\{X=1,Y=0\} = P\{X=1\} \cdot P\{Y=0\} = \frac{2}{5} \cdot \frac{3}{5} = \frac{6}{25}\)
\(P\{X=1,Y=1\} = P\{X=1\} \cdot P\{Y=1\} = \frac{2}{5} \cdot \frac{2}{5} = \frac{4}{25}\)
综上,\((X,Y)\)的分布律及边缘分布律为:
| X | Y | Y | \(p_{i\cdot}\) |
|---|---|---|---|
| X | 0 | 1 | \(p_{i\cdot}\) |
| 0 | \(\frac{9}{25}\) | \(\frac{6}{25}\) | \(\frac{3}{5}\) |
| 1 | \(\frac{6}{25}\) | \(\frac{4}{25}\) | \(\frac{2}{5}\) |
| \(p_{\cdot j}\) | \(\frac{3}{5}\) | \(\frac{2}{5}\) | 1 |
(2)不放回地取球情形
记事件\(\{X=1\}\)表示第一次取球取到的是红球,\(\{X=0\}\)表示第一次取球取到的是白球,则\(X\)的分布律为:
\(P\{X=1\} = \frac{2}{5},\ \ P\{X=0\} = \frac{3}{5}\);
同理,记事件\(\{Y=1\}\)表示第二次取球取到的是红球,\(\{Y=0\}\)表示第二次取球取到的是白球,但\(Y\)的分布律受\(X\)取值的影响:
当\(X=1\)时:\(P\{Y=1\} = \frac{1}{4},\ \ P\{Y=0\} = \frac{3}{4}\);
当\(X=0\)时:\(P\{Y=1\} = \frac{2}{4},\ \ P\{Y=0\} = \frac{2}{4}\);
因执行的是不放回地取球,因此随机事件\(X\)与\(Y\)并不是相互独立,所以:
\(P\{X=0,Y=0\} = P\{X=0\} \cdot P\{Y=0\} = \frac{3}{5} \cdot \frac{2}{4} = \frac{3}{10}\)
\(P\{X=0,Y=1\} = P\{X=0\} \cdot P\{Y=1\} = \frac{3}{5} \cdot \frac{2}{4} = \frac{3}{10}\)
\(P\{X=1,Y=0\} = P\{X=1\} \cdot P\{Y=0\} = \frac{2}{5} \cdot \frac{3}{4} = \frac{3}{10}\)
\(P\{X=1,Y=1\} = P\{X=1\} \cdot P\{Y=1\} = \frac{2}{5} \cdot \frac{1}{4} = \frac{1}{10}\)
综上,\((X,Y)\)的分布律及边缘分布律为:
| X | Y | Y | \(p_{i\cdot}\) |
|---|---|---|---|
| X | 0 | 1 | \(p_{i\cdot}\) |
| 0 | \(\frac{3}{10}\) | \(\frac{3}{10}\) | \(\frac{3}{5}\) |
| 1 | \(\frac{3}{10}\) | \(\frac{1}{10}\) | \(\frac{2}{5}\) |
| \(p_{\cdot j}\) | \(\frac{3}{5}\) | \(\frac{2}{5}\) | 1 |
由此可见,对于有放回和不放回取样\((X,Y)\)的边缘分布律完全相同,但是\((X,Y)\)的分布律却不相同,这表明\((X,Y)\)的分布律不仅反映了两个分量的概率分布,还反映了\(X\)与\(Y\)之间的关系;因此,在研究二维随机变量时,不仅要考察两个分量各自的概率性质,还要考虑他们之间的关系,即,将\((X,Y)\)作为一个整体来研究。
1.3 二维连续型随机变量的概率密度和连续概率密度
定义5: 设二维连续型随机变量\((X,Y)\)的分布函数\(F(x,y)\),若存在非负可积的二元函数\(f(x,y)\),使得对于任意的\(x,y\)都有:
\(F(x,y) = \int_{-\infty}^{x} \int_{-\infty}^{y}f(u,v) dudv\) ,
则称\(f(x,y)\)是\((X,Y)\)的概率密度函数或者简称为:概率密度。
\((X,Y)\)的概率密度\(f(x,y)\)满足以下性质:
①非负性:\(f(x,y) \ge 0\)
②规范性:\(\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty}f(x,y) dxdy = 1\)
③若\(f(x,y)\)在点\((x,y)\)处连续,则有:
\(\frac{\partial^2 F(x,y)}{\partial{x} \partial{y}} = f(x,y)\)
④设\(D\)是\(XOY\)平面上的一个区域,则二维随机变量\((X,Y)\)落在\(D\)内的概率为\(P\{(X,Y) \in D\} = \iint_{D} f(x,y) dxdy\)
例7:设二维随机变量\((X,Y)\)的概率密度为:
求\((X,Y)\)的分布函数\(F(x,y)\)。
解:当\(x \le 0\)或\(y \le 0\)时有:\(F(x,y) = 0\);
当\(x \gt 0, y \gt 0\)时有:
所以,\((X,Y)\)的分布函数为:
例8:设二维随机变量\((X,Y)\)的分布函数为:\(F(x,y) = a(b + \arctan{x})(c + \arctan{y}),\ \ -\infty \lt x,y \lt +\infty\) ;
求(1)常数\(a,b,c\); (2)\((X,Y)\)的概率密度。
解:(1)由分布函数的性质可知:
\(F(+\infty,\ +\infty) = 1 = a(b + \frac{\pi}{2})(c+\frac{\pi}{2})\)
\(F(x,\ -\infty) = 0 = a(b + \arctan{x})(c - \frac{\pi}{2})\)
\(F(-\infty,\ y) = 0 = a(b - \frac{\pi}{2})(c + \arctan{y})\)
得:\(a = \frac{1}{\pi^2},\ \ b = \frac{\pi}{2},\ \ c = \frac{\pi}{2}\)
(2)由以上知,\((X,Y)\)的分布函数为:\(F(x,y) = \frac{1}{\pi^2}(\frac{\pi}{2} + \arctan{x})(\frac{\pi}{2} + \arctan{y}),\ \ -\infty \lt x,y \lt +\infty\) ;
所以其概率密度为:\(F(x,y) = \frac{1}{\pi^2} \cdot \frac{1}{1+x^2} \cdot \frac{1}{1+y^2} = \frac{1}{\pi^2(1+x^2)(1+y^2)},\ \ -\infty \lt x,y \lt +\infty\)
定义6:设\(D\)是平面上的一个区域,其面积\(S \gt 0\),若二维连续型随机变量\((X,Y)\)的概率密度为:
则称\((X,Y)\)在区域\(D\)上服从均匀分布,记作\((X,Y) \sim U(D)\)。
若\((X,Y) \sim U(D),\ \ D_1 \subset D\),\(D_1\)的面积为\(S_1\),则\(P\{(x,y) \in D_1\} = \frac{S_1}{S}\);特别地,有以下两种情形:
①\(D\)是矩形区域,\(a \lt x \le b,\ c \lt y \le d,\ (X,Y) \sim U(D)\);则\((X,Y)\)的概率密度为:
②\(D\)是圆形区域,\(x^2 + y^2 \le R^2,\ (X,Y) \sim U(D)\);则\((X,Y)\)的概率密度为:
\(\bigstar \bigstar \bigstar \bigstar \bigstar\) 一句话就是:落在区域内,其概率密度就是\(\frac{1}{S}\);各种规则的区域有现成的面积公式,不规则的区域就是要微积分的方法计算面积。
例9:设二维随机变量\((X,Y)\)在区域\(D = \{(x,y) | y \le x,\ 0 \le x \le 1,\ y \ge 0\}\)上服从均匀分布,求\(P\{X+Y \le 1\}\)。
解:涉及到二重积分的问题建议首先画图:
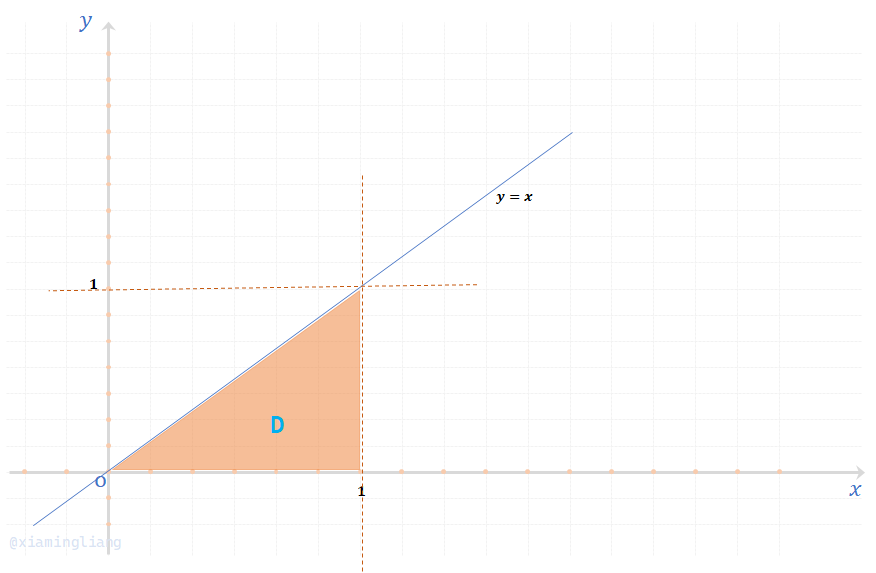
区域D的面积:\(S = \frac{1}{2}\);由题目知,\((X,Y) \sim U(D)\),则其概率密度为:
需要求的\(P\{X+Y \le 1\}\)代表的是\((x,y)\)落在\(x+y \le 1\)区域\(D_1\)内的概率,在图中描述为:(忽略途中坐标比例问题_)
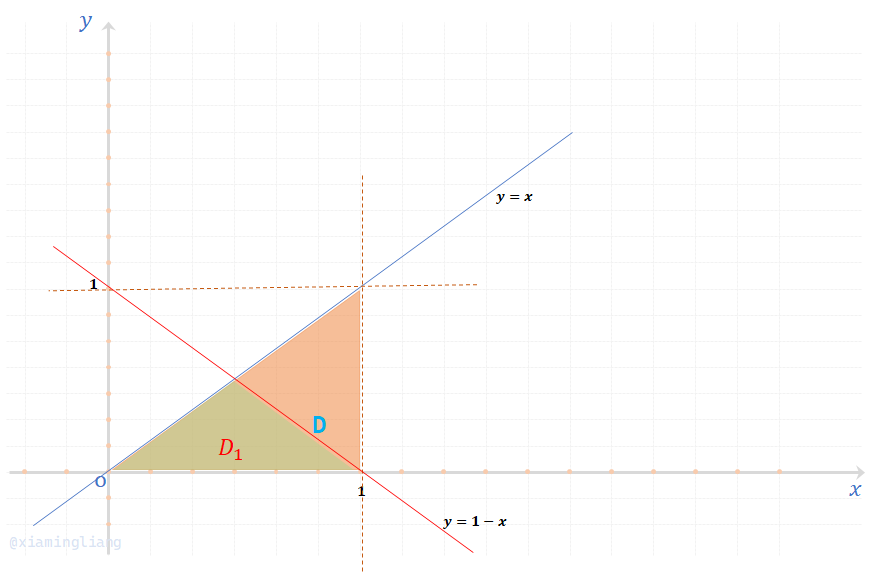
则:\(P\{X+Y \le 1\} = \iint_{x+1 \le 1}f(x,y)dxdy = \iint_{D_1} f(x,y) dxdy = \iint_{D_1} 2 dxdy\)
当然我们可以利用二重积分的只是解得最终结果,但更方面的是,我们可以直接根据\(\iint_{D_1} 1dxdy = S_{D_1}\)的实际意义得出:
\(P\{X+Y \le 1\} = 2S_{D_1} = \frac{1}{4}\)
<文章太长,要求分页~~>
本文来自博客园,作者:夏明亮,转载请注明原文链接:https://www.cnblogs.com/xiaml/articles/18674562


 浙公网安备 33010602011771号
浙公网安备 33010602011771号