【概率论与数理统计】第二章 随机变量及其分布

第二章 随机变量及其分布

第一章种学习了随机现象、随机试验、随机事件等概念，讨论了随机事件的关系、运算以及概率；且只考虑了个别事件下的频率问题。接下来，进一步第需要建立随机试验结果与实数的对应关系，这类似于函数的映射，我们称之为随机变量，以便使用高等数学的方法来研究随机试验。

1 离散型随机变量

1.1 随机变量的概念

随机变量的数学定义：

定义1：设\(E\)为随机试验，\(\Omega\)为其样本空间，若对于每一个结果(样本点)\(\omega \in \Omega\)，都有一个实数\(X(\omega)\)与之对应；这样就得到一个定义在\(\Omega\)上的实值函数\(X = X(\omega)\)，称为随机变量；随机变量通常用\(X、Y、Z\)或者\(X_1,X_2,...\)来表示。

注意：对于一个随机试验可以有与之关联的多个随机变量，而不是仅有一个；随着不同研究的需要，我们可以定义不同的随机变量。

我们可以试验随机变量描述事件，例如：在掷硬币试验中\(\{X=1\}\)表示"出现正面"，\(\{X=0\}\)表示"出现反面"且\(P\{X=1\} = \frac{1}{2}\)。

当然：\(\{X=1\}、\{X=0\}\)只是习惯的、相对较为普遍的用法并不是唯一的用法；我们使用\(\{X=100\}\)表示"出现正面"，\(\{X=200\}\)表示"出现反面"是完全没有问题且正确的，只是不那么习惯而已。

在掷骰子试验中，我们可以使用\(\{X=6\}\)表示"出现6点"，\(P\{X=6\} = \frac{1}{6}\)；使用\(\{X \ge 4\}\)表示"出现4/5/6点"，\(\{X \ge 4\} = \{X = 4,5,6\}\)，\(P\{X \ge 4\} = \frac{1}{2}\)。

1.2 离散型随机变量及其分布律

随机变量的取值可能是有限个，也可能是无限个。

定义2：若随机变量\(X\)只取有限多个或可列的无限多个值(可以枚举表示的)，则称\(X\)为离散型随机变量。

大白话就是值是一个个的，颗粒状的，不连续的。

定义 设\(X\)为离散型随机变量，可能的取值为\(X_1,X_2,...,X_k,...\)，且\(P\{X=x_k\} = P_k,\ \ k=1,2,3,...\)，则称其为\(X\)的分布律或分布列或者概率分布。

分布律也可以使用表格形式表达：

X	\(X_1\)	\(X_2\)	\(X_3\)	...	\(X_k\)	...
P	\(p_1\)	\(p_2\)	\(p_3\)	...	\(p_k\)	...

分布律\(\{p_k\}\)具有以下性质：

(1) \(p_k, \ \ \ k=1,2,...\)； # \(p_k\)是概率嘛

(2) \(\sum_{k=1}^{\infin} p_k = 1\); # \(\{X=X_k\},\ \ k=1,2,...\)之间是互不相容的事件，且\(\cup_{k=1}^{\infin} \{X=X_k\} = \Omega\)。

反之，若某数列\(\{p_k\}\)具有以上两条性质，则他们必可作为某随机变量的分布律。

例1：设离散型随机变量\(X\)的分布律为：

X	0	1	2
P	0.2	c	0.5

求常数c。

解：由分布律的性质知：\(0.2+c+0.5 = 1 ;\ \ \ \ \therefore c=0.3\)。

例2：掷一枚质地均匀的骰子，这\(X\)为出现的点数，求\(X\)的分布律。

解：\(X\)全部可能的取值为"1, 2, 3, 4, 5, 6"，且\(p_k = p\{X=k\} = \frac{1}{6},\ \ \ \ k=1,2,3,4,5,6\)；则\(X\)的分布律为：

X	1	2	3	4	5	6
P	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)

技巧：首先找出随机变量所有可能的取值，然后求出每个取值对应的概率，做成表格即可。

$\bigstar \bigstar \(**例3：袋中由编号1~5的5个球，从中取3个，这\)X\(为取出的球中的最大编号，求\)X$的分布律。**

解：\(X\)全部可能的取值为"3, 4, 5"；用古典概型计算概率：

\(P\{X=3\} = \frac{C_2^2}{C_5^3} = \frac{1}{10}\) # 分母：全部5个球中取3个；分子：如果最大球是3，3已经确定取出，只有从1，2这2球中取另外2个。

\(P\{X = 4\} = \frac{C_3^2}{C_5^3} = \frac{3}{10}\)

\(P\{X=5\} = \frac{C_4^2}{C_5^3} = \frac{6}{10}\)

因此\(X\)的分布律如下：

X	3	4	5
P	\(\frac{1}{10}\)	\(\frac{3}{10}\)	\(\frac{6}{10}\)

$\bigstar \bigstar \(**例4：已知一批零件10个，其中3个不合格，今任取一个，若取到不合格的就丢掉，再重新取一个，如此下去，试求取到合格零件之前取出的不合格零件个数\)X$的分布律。**

解：\(X\)可能的取值是："0, 1, 2, 3"；设\(A_i\)表示"第\(i\)次取出的零件不合格，\(i=1,2,3,4\)"。

\(P\{X=0\} = P(\overline{A_1}) = \frac{7}{10}\)

\(P\{X=1\}=P(A_1 \overline{A_2}) = P(A_1)P(\overline{A_2} | A_1) = \frac{3}{10} \times \frac{7}{9} = \frac{7}{30}\)

\(P\{X=2\} = P(A_1 A_3 \overline{A_3}) = P(A_1)P(A2|A_1)P(\overline{A_3} | A_1 A_2) = \frac{3}{10} \times \frac{2}{9} \times \frac{7}{8} = \frac{7}{120}\)

\(P\{X=3\} = P(A_1 A_2 A_3 \overline{A_4}) = P(A_1)P(A_2| A_1)P(A_3|A_1 A_2)P(\overline{A_4} | A_1 A_2 A_3) = \frac{3}{10} \times \frac{2}{9} \times \frac{1}{8} \times \frac{7}{7} = \frac{1}{120}\)

故\(X\)的分布律为：

X	0	1	2	3
P	\(\frac{7}{10}\)	\(\frac{7}{30}\)	\(\frac{7}{120}\)	\(\frac{1}{120}\)

若需要求\(X\)满足某一条件这样的事件概率，例如例2中要求掷出的点数是奇数的概率，则应将满足条件的所有\(X\)对应的概率相加即可。

1.3 0-1分布与二项分布

下面介绍三种重要的常用离散型随机变量，它们是：\(0-1\)分布、二项分布和泊松分布。

定义4：若随机变量\(X\)只取两个可能的值0，1；且\(P\{X=1\} = p,\ \ P\{X=0\}=q\)，其中\(0 \lt p \lt 1,\ \ q=1-p\)；则称\(X\)服从\(0-1\)分布；\(X\)的分布律为：

X	0	1
P	\(q\)	\(p\)

在\(n\)重伯努利试验中，每轮试验只观察\(A\)是否发生，定义随机变量\(X\)：

\[X = \begin{cases} 0 , &当A发生\\ 1 , &当A不发生 \end{cases} \]

大白话：任何只有两种结果是试验，或者说我们研究的结果只有两种的试验；比如：掷硬币，研究结果的正反面；掷骰子，但只研究结果的奇数还是偶数等。

定义5：若随机变量\(X\)的可能值为0，1，...，n；n为正整数，而\(X\)的分布律为：\(p_k = P\{X=k\} = C_n^k p^k q^{n-k}, \ \ k=0,1,...,n\)；其中，\(0 \lt p \lt 1,\ q = 1 - p\)，则称\(X\)服从参数为\(n,p\)的二项分布，记作：\(X \sim B(n, p)\)</u>。

显然，当\(n=1\)时，\(X\)服从\(0-1\)分布，即\(X \sim B(1, p)\)；【满足\(0-1\)分布每次试验都只可能有0、1两个结果，p并不一定非要是1/2】；即\(0-1\)分布是二项分布的一种特例。

但是满足二项分布的每次试验结果不止2个。这是本质区别！！

在\(n\)重伯努利试验中，令\(X\)代表\(A\)的发生次数，则\(P\{X=k\} = P_n(k) = C_n^k p^k q^{n-k},\ \ k=0,1,2,...,n\)；即\(X\)服从参数为\(n, p\)的二项分布。

这里特别特别要注意："随机变量\(X\)的可能值为0，1，...，n；n为正整数"中\(X\)的取值个数从0开始计算一共有\(n+1\)个；注意这里不要犯迷糊，\(n\)代表的是"最大可能取值个数-1"！！

二项分布名称的由来：（补充下数学知识！！）

二项式\((p+q)^n\)的展开式中：

\[\begin{aligned} (p + q)^n = C_n^0 q^0 p^n + C_n^1 q^1 p^{n-1} + C_n^2 q^2 p^{n-2} + ... + C_n^n q^n p^0 = \sum_{k=0}^n C_n^k q^k p^{n-k}\\ \end{aligned} \]

由于\(p+q = q+p\)；因此上述的二项式展开式等价于：(而且：\(C_n^k = C_n^{n-k}\)的)

\[(p + q)^n = (q + p)^n = C_n^0 p^0 q^n + C_n^1 p^1 q^{n-1} + C_n^2 p^2 q^{n-2} + ... + C_n^n p^n q^0 = \sum_{k=0}^n C_n^k p^k q^{n-k} \]

其中的第\(k+1\)项（\(C_n^0 p^0 q^n\)是第1项）恰好是\(C_n^k p^k q^{n-k}\)，这与\(P\{X=k\}\)正好相同，因此称为符合二项分布。

因为\(P\{X=k\} = C_n^k p^k q^{n-k}, \ \ k=0,1,...,n\)的所有取值的概率之和为1，即$\sum_{k=0}^n p_k = \sum_{k=0}^n P{X=k} = \sum_{k=0}^n C_n^k p^k q^{n-k} = (p + q)^n = 1 $，这满足分布律的基本性质。

大白话：由以上描述可见，任何有确定个数结果的试验，都可以视为满足二项分布。这就包含的范围非常广泛了！！

无限个可能结果的试验，我们先不考虑！！

对于任意的正整数\(n\)，\((a + b)^n = \sum_{k=0}^n C_n^k a^n b^{n-k}\)，其中\(C_n^k\)称为二项式系数；\(C_n^k = \frac{n!}{k!(n-k)!}\)。

$\bigstar \bigstar $例5：某特效药临床有效率为0.95，今10人服用，问至少有8人被治愈的概率？

解：设\(X\)为"10人中治愈的人数"，由题目知\(X \sim B(10, 0.95)\) ## X可能的值有10个，每次独立试验的有效率0.95

这里再次特别提醒，不要嫌我啰嗦；这个\(n=10\)是指X可能取值为"有0，1，2，3，4，5，6，7，8，9，10个人被治愈"的11个可能值中的最后一个值，因为从0开始计数，千万不要把\(n\)理解为11了！！！

\(P\{X \ge 8\} = P\{X=8\} + P\{X=9\} + P\{X=10\} = C_{10}^8(0.95)^8(0.05)^2 + C_{10}^9(0.95)^9(0.05)^1 + C_{10}^{10}(0.95)^10(0.05)^0 = 0.9885\)

$\bigstar \bigstar \(**例6：设\)X \sim B(2,p),\ Y \sim B(3, p)\(；设\)p{X \ge 1} = \frac{5}{9}\(，求\)P{Y \ge 1}$。**

解：由\(P\{X \ge 1\} = \frac{5}{9}\)知\(X\)可能的取值有"0，1，2"三种可能，因此，\(P\{X=0\} = 1 - P\{X \ge 1\} = \frac{4}{9}\)；

\(\therefore \ P\{X=0\} = C_2^0 p^0 (1-p)^2 = \frac{4}{9}\)； 又\(\because C_2^0 = 1 ;\ \ p^0 = 1\) ；

\(\therefore \ (1-p)^2 = \frac{4}{9}\)；

\(\therefore \ p = \frac{1}{3}\)

由\(Y \sim B(3, p)\)可知\(Y\)可能的取值有"0，1，2，3"四种可能，因此，\(P\{Y \ge 1\} = 1 - P\{Y = 0\} = 1 - C_3^0 p^0 (1-p)^3 = 1 - \frac{8}{27} = \frac{19}{27}\)。

由此可见，二项分布的计算很繁琐，尤其是出现例如：\(n=1000,\ p=0.05\)时；\(C_{1000}^{10}(0.05)^10(0.95)^{990}\)这类的计算，因此，需要寻求近似计算的方法；下面给给出一个\(n\)很大，\(p\)很小的近似计算公式，这就是著名的二项分布的泊松逼近。

泊松(Possion)定理：设\(\lambda \gt 0\)是常数，\(n\)为任意正整数，在\(n\)重伯努利试验中，假设事件\(A\)在一次试验中发生的概率是\(p_n\)，当\(n \to +\infty\)时，有\(np_n \to \lambda\)，则对于任意取定的非负整数\(k\)，有：\(\lim_{n \to +\infty} C_n^k p_n^k (1-p_k)^{n-k} = \frac{\lambda^k}{k!} e^{-\lambda}\)。

这里只给出结论，不给出证明过程；有兴趣的可以查阅相关资料。

由泊松定理知，当\(n\)很大，\(p\)很小时由近似公式：

\(C_n^k p^k q^{n-k} \approx \frac{\lambda^k}{k!} e^{-\lambda}, \ \ 其中，\lambda = np, q = 1-p\)。

在实际中，当\(n \ge 20,\ p \le 0.05\)时使用该近似公式的效果更佳。

\(\frac{\lambda^k}{k!} e^{-\lambda}\)的值可以通过泊松表查询；泊松表给出了已知\(\lambda\)和\(k\)值对应的\(\sum_{k}^{+\infty} \frac{\lambda^k}{k!} e^{-\lambda}\)值查询。 ## 特别注意：表里的值是从\(k\)开始到\(+\infty\)的累加和哦，下线不一定是0，但上限一定是\(+\infty\)。

例7：一个工厂的产品废品率为0.005，任取1000件，计算：

(1) 至少有2件废品的概率

(2) 不超过5件废品的概率

解：设\(X\)表示"取出1000件中包含的废品总数"，则\(X \sim B(1000, 0.005)\)；利用近似公式：\(\lambda = np = 5\)；

(1) $P{X \ge 2} = 1 - P{X=0} - P{X=1} = 1- C_{1000}^{0} (0.005)^0(0.995) - C_{1000}^{1} (0.005)^1(0.995) $

\(\approx 1- \frac{\lambda^0}{0!} e^{-\lambda} - \frac{\lambda^1}{1!} e^{-\lambda} = 1- \frac{5^0}{0!} e^{-5} - \frac{5^1}{1!} e^{-5} = 0.9596\)

(2) \(P\{X \le 5\} = \sum_{k=0}^5 P\{X=k\} = \sum_{k=0}^{5} C_{1000}^k (0.005)^k (0.995)^{1000-k}\)

\(\approx \sum_{k=0}^5 \frac{\lambda^k}{k!} e^{-\lambda} = 1 - \sum_{k=6}^{\infty} \frac{\lambda^k}{k!} e^{-\lambda}\) ## 这里有个转换关系需要特别注意。转换后才可以查泊松表，按照\(\lambda = 5, k = 6\)查询！！

\(= 0.6160\)

1.4 泊松分布

定义6：随机变量\(X\)的可能取值"0，1，2，...，n，..."；而\(X\)的分布律为：

\(p_k = P\{X=k\} = \frac{\lambda^k}{k!} e^{-\lambda},\ \ \ \ k=0,1,2,...\)

其中，\(\lambda \gt 0\)，则称\(X\)服从参数为\(\lambda\)的泊松分布，简记为：\(X \sim P(\lambda)\)。

大白话，与二项分布相比，\(S\)的取值变成的无限个（当然仍旧是离散型的）；因此\(n \to \infty\)；导致符合泊松定理的近似计算公式，从而产生常数\(\lambda = np\)；使得概率仅与\(\lambda和k\)有关。

由\(\sum_{k=0}^{\infty} p_k = \sum_{k=0}^{\infty} \frac{\lambda^k}{k!} e^{-\lambda} = e^{-\lambda} \sum_{k=0}^{\infty} \frac{\lambda^k}{k!} = e^{-\lambda} e^{\lambda} = 1\)可知\(\{p_k\}\)满足分布律的基本性质。

泊松分布是二项分布的极限分布(\(n \to \infty\)的情况下)，非常重要！！

例8：设随机变量\(X\)服从参数为5的泊松分布，求：

(1) \(P\{X=10\}\)

(2) \(P\{X \le 10\}\)

解：(1) 查询泊松表，找\(\lambda = 5列,\ X=10行\)对应的值；和\(\lambda = 5列,\ X=11行\)对应的值：

\(P\{X=10\} = P\{X \ge 10\} - P\{X \ge 11\} = \sum_{k=10}^{\infty} \frac{\lambda^k}{k!} e^{-\lambda} -\sum_{k=11}^{\infty} \frac{\lambda^k}{k!} e^{-\lambda} \approx 0.018133\)

(2) \(P\{X \le 10\} = 1- P\{X \ge 11\} = 1 - \sum_{k=11}^{\infty} \frac{\lambda^k}{k!} e^{-\lambda} \approx 0.986305\)

例9：设\(X\)服从泊松分布，且已知\(P\{X=1\} = P\{X=2\}\)；求\(P\{X=4\}\)。

解：设参数为\(\lambda\)，则：

\(P\{X=1\} = \frac{\lambda^1}{1!} e^{-\lambda} = \lambda e^{-\lambda}\)

\(P\{X=2\} = \frac{\lambda^2}{2!} e^{-\lambda} = \frac{\lambda^2}{2} e^{-\lambda}\)

由题目知：\(P\{X=1\} = P\{X=2\}\) 得 \(\lambda = 2\)

\(\therefore \ P\{X=4\} = \frac{\lambda^4}{4!} e^{-\lambda} = \frac{2^4}{4!} e^{-2} = \frac{2}{3} e^{-2}\)

2 随机变量的分布函数

2.1 分布函数的概念

对于非离散型得随机变量就无法用分布律来描述它了。

首先，我们不能将其所有可能的取值一一地列举出来，如连续型随机变量的取值可充满数轴的一个区间\((a,b)\)，甚至是\(n\)个区间，也可以是无穷区间；其次，对于连续型随机变量\(X\)，任取一指定实数值\(x\)的概率是0，即\(P\{X=x\}=0\)。

我解释下，因为连续型随机变量\(X\)的取值在某个或很多个区间内，那取值的个数就是无限个，在无限个可能中\(x\)仅仅是其中一个，因此，仅仅这一个取值对应的概率就是0。

于是，如何刻画一般的随机变量的统计规律就成了我们的首要问题。

在实际应用中，如测量某物理量的误差\(\xi\)，测量灯泡寿命\(\tau\)等这样的随机变量，我们并不会对误差或寿命的某一特定值的概率感兴趣，而是考虑误差落在某个区间的概率，寿命大于某个数的概率之类的。

对于随机变量\(X\)，我们关心诸如事件\(\{X \le x\},\ \{X \gt x\},\ \{x_1 \lt X \le x_2\}\)等的概率，但是由于$ x_1 \le x_2\(，且\){X \le x_1} \subset {X \le x_2}\(；所以：\){x_1 \lt X \le x_2} = {X \le x_2} - {X \le x_1}$。

又因\(\{X \gt x\}\)的对立事件为\(\{X \le x\}\)，所以：\(P\{X \gt x\} = 1 - P\{X \le x\}\)。

因此，\(\{X \le x\}\)的概率\(P\{X \le x\}\)成了关键的角色，我们记\(F(x) = P\{X \le x\}\)，任意给定的\(x \in (-\infty,+\infty)\)，对应的\(F(x)\)是一个概率。\(P\{X \le x\} \in [0,1]\)，说明\(F(x)\)是定义在\((-\infty,+\infty)\)上的普通实值函数，从而引出随机变量分布函数的定义。

解释下，上面任何不等式中\(\le和\lt\)、\(\ge和\gt\)是分别等价的；因为\(=\)对应值的概率是0，所以有没有\(=\)并不影响计算结果。

定义7：设\(X\)为随机变量，称函数\(F(x)=P\{X \le x\},\ \ x \in (-\infty,+\infty)\)为\(X\)的分布函数。

注意：随机变量的分布函数定义适用于任意随机变量，包括离散型随机变量；因此，离散型随机变量既有分布律又有分布函数。

当\(X\)为离散型随机变量时，设\(X\)的分布律为：\(p_k = P\{X=k\},\ \ k=0,1,2,...\)。

由于\(\{X \le x\} = \cup_{x_k \le x} \{X = x_k\}\)，由概率性质知：\(F(x) = P\{X \le x\} = \sum_{x_k \le x} \{X = x_k\} = \sum_{x_k \le x} p_k\)即：\(F(x) = \sum_{x_k \le x} p_k\)。

这是在微观上将连续型的取值看作时更小颗粒度的离散装的取值，从而得出的结论。底层逻辑是：为什么连续？因为颗粒度足够小。

例1：离散型随机变量\(X\)的分布律为：

X	-1	0	1	2
P	0.2	0.1	0.3	0.4

求\(X\)的分布函数。

解：当\(x \lt -1\)时\(F(x) = P\{X \le x\} = 0\)

当\(-1 \le x \lt 0\)时\(F(x) = P\{X \le x\} = P\{X = -1\} = 0.2\)

当\(0 \le x \lt 1\)时\(F(x) = P\{X \le x\} = P\{X = -1\} + P\{X=0\} = 0.2+0.1 = 0.3\)

当\(1 \le x \lt 2\)时\(F(x) = P\{X \le x\} = P\{X = -1\} + P\{X=0\} + P\{X=1\} = 0.2 + 0.1 + 0.3 = 0.6\)

当\(x \ge 2\)时\(F(x) = P\{X \le x\} = P\{X = -1\} + P\{X=0\} + P\{X=1\} + P\{X=2\} = 0.2+0.1+0.3+0.4=1\)

特别注意，看清\(F(x)\)作为分布函数的定义；无论何时它都代表\(X \le x\)的概率，只不过\(x\)是由定义域的变量而已。

还需要注意，对于离散型随机变量的分布函数要特别关注取值边界，特别关注\(=\)敌营的取值是否被包含。

因此，\(X\)的分布函数为：

\[F(x)= \begin{cases} 0, &x\lt 1 \\ 0.2, &-1 \le x \lt 0 \\ 0.3, &0 \le x \lt 1 \\ 0.6, &1 \le x \lt 2 \\ 1, &x \ge 2 \end{cases} \]

其图像为：

2.2 分布函数的性质

① \(0 \le F(x) \le 1\)

② \(F(x)\)不是减函数，即对于任意\(x_1 \lt x_2\)都有\(F(x_1) \le F(x_2)\)；

③ \(F(-\infty) = 0,\ F(+\infty) = 1\)即\(\lim_{x \to -\infty} F(x) = 0,\ \lim_{x \to -\infty} F(x) = 1\)；

④ \(F(x)\)右连续，即\(\lim_{\Delta{x} \to 0^+} F(x + \Delta{x}) = F(x)\)。

例2：设随机变量\(X\)的分布函数为：

\[F(x)= \begin{cases} a + be^{-\lambda x}, & x>0 \\ 0, & x\le 0 \end{cases} \]

其中，\(\lambda \gt 0\)为常数，求常数\(a\)和\(b\)的值。

解：由题意有：\(F(+\infty) =\lim_{x \to +\infty} F(x) = \lim_{x \to +\infty} (a + be^{-\lambda x}) = a\)

由分布函数性质\(F(+\infty) = 1\)得\(a = 1\)

由\(F(x)\)的右连接性得：\(F(0+0) = \lim_{\Delta x \to 0^+} F(x) = \lim_{\Delta x \to 0} (a + be^{-\lambda 0}) = a + b = 0\) # 从x=0左侧不断逼近0出的极限值与x=0处的值相同(不中断)！

所以：\(b = -1\)

因此：\(a = 1,\ b = -1\)。

补充下数学知识：自然常数，符号\(e\)，为数学中一个常数，是一个无限不循环小数，且为超越数，其值约为2.718281828459045。它是自然对数函数的底数。有时称它为欧拉数，以瑞士数学家欧拉命名。

\(e\)作为数学常数，它的其中一个定义是：\(e = \lim_{x \to \infty}(1 + \frac{1}{x})^x\)。

同时：\(e = \sum_{n=0}^{\infty} \frac{1}{n!} = \frac{1}{0!} + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + ...\)。 注意：\(0! = 1,\ 1! =1\)。

在已知\(X\)的分布函数\(F(x)\)情况下，我们可知以下重要事件的概率：

① \(P\{X \le b\} = F(b)\)

② \(P\{a \lt X \le b\} = F(b) - F(a)\)

③ \(P\{X \gt b\} = 1 - P\{X \le b\} = 1- F(b)\)

例3：设随机变量\(X\)的分布函数为：

\[F(x) = \begin{cases} 0, & x \lt 0 \\ \frac{x}{3}, & 0 \le x \lt 1 \\ \frac{x}{2}, & 1 \le x \lt 2 \\ 1, & x \ge 2 \end{cases} \]

求：(1) \(P\{\frac{1}{2} \lt X \le \frac{3}{2}\}\) (2) \(P\{ X \gt \frac{1}{2}\}\) (3) \(P\{ X \gt \frac{3}{2}\}\)

解：(1) \(P\{\frac{1}{2} \lt x \le \frac{3}{2}\} = F(\frac{3}{2}) - F(\frac{1}{2}) = \frac{3}{4} - \frac{1}{6} = \frac{7}{12}\)

(2) \(P\{X \gt \frac{1}{2}\} = 1 - F(\frac{1}{2}) = 1 - \frac{1}{6} = \frac{5}{6}\)

(3) \(P\{X \gt \frac{3}{2}\} = 1 - F(\frac{3}{2}) = 1 - \frac{3}{4} = \frac{1}{4}\)

3 连续型随机变量及其概率密度

3.1 连续型随机变量及其概率密度

前面已经多次提到连续型随机变量，下面给出定义：

定义8：对于随机变量\(X\)的分布函数\(F(x)\)，存在非负数\(f(x)\)使得对于任意实数\(x\)有：\(F(x) = \int_{-\infty}^{x} f(t)dt\)；则称\(X\)为连续型随机变量，并称\(f(x)\)是\(X\)的概率密度函数，简称概率密度。

补充高等数学知识：\(F(x) = \int_{-\infty}^{x} f(t)dt\)的计算方法：

1.找到\(f(t)\)对应的原函数\(g(t)\)，即\(g(t)的导函数g'(t) = f(t)\)；

2.根据积分\(\int_{-\infty}^x\)给出的积分上限\(x\)和积分下限\(-\infty\)带入\(g(t)\)；并计算\(g(x) - g(-\infty)\)；

3.计算结果即为\(F(x)\)。

上述积分等式，我们通过高等数学的知识，当\(f(x)\)可积时，连续型随机变量的分布函数\(F(x)\)是连续函数，进一步，对任意的实数\(x\)，\(\Delta x \gt 0\)有：\(0 \le P\{X=x\} \le P\{x - \Delta x \lt X \le x\} = F(x) - F(x-\Delta x)\)

由于\(F(x)\)为连续函数，令\(\Delta \to 0\)，则\(P\{X = x\} = 0\)；即连续型随机变量得某一指定点取值的概率为0.

有定义8和分布函数的性质可得下列概率密度的性质：

(1) \(f(x) \ge 0\)

(2) \(\int_{-\infty}^{+\infty} f(x)dx = 1\)

且满足以上两条性质的函数一定是某个连续型随机变量的概率密度。

(3) \(P\{a \lt X \le b\} = F(b) - F(a) = \int_{a}^{b} f(x)dx\)

(4) 设\(x\)是\(f(x)\)的连续点，则\(F'(x)\)存在，且：\(F'(x) = f(x)\) $\bigstar \bigstar \bigstar \bigstar \bigstar $

根据积分的几何意义，性质(2)意为介于曲线\(y=f(x)\)与\(x\)轴之间的面积为1；

由性质(3)知\(X\)落在区间\((a,b]\)的概率\(P\{a \lt x \lt b\}\)就是由曲线\(y = f(x),\ x = a,\ x = b\)围成的曲边梯形的面积，如图阴影部分所示：

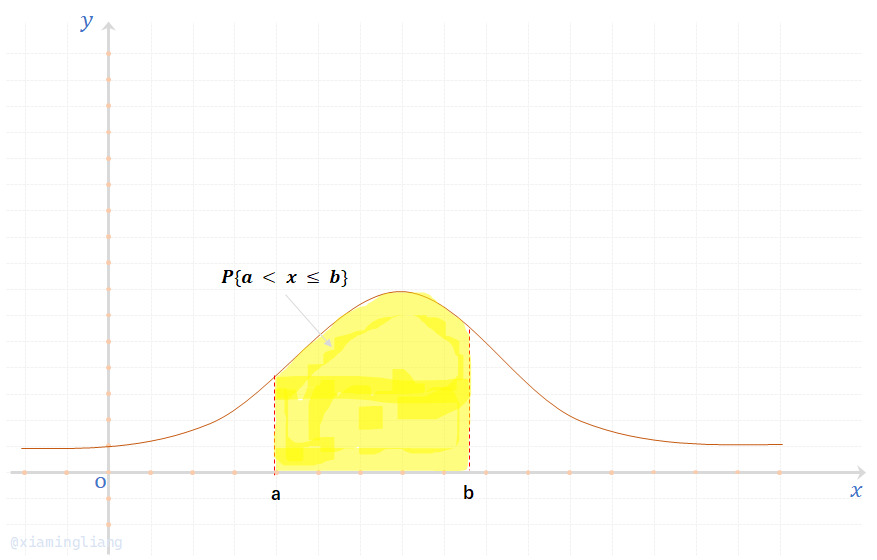
由性质(4)，在\(f(x)\)的连续点\(x\)处有：

\(f(x) = \lim_{\Delta x \to 0^+} \frac{F(x + \Delta x) - F(x)}{\Delta x} = \lim_{\Delta x \to 0^+} \frac{P\{x \lt X \le x+\Delta x\}}{\Delta x}\)

即\(f(x)\)为\(X\)落在区间\((x,x+\Delta x]\)的概率与区间长度的比值。

从这里我们可以看到概率密度的定义与物理学中线密度的定义相似，这就是为什么称\(f(x)\)为概率密度的原因。

\(\bigstar \bigstar \bigstar \bigstar \bigstar\)例1：设随机变量\(X\)的概率密度为：

\[f(x) = \begin{cases} ax, & 0 \le x \le 1 \\ 0, & 其他 \end{cases} \]

求：(1) 常数\(a\)； (2) 分布函数\(F(x)\)； (3) \(P\{|X| \le \frac{1}{2}\}\)。

解：(1)由概率密度的性质\(\int_{-\infty}^{+\infty} f(x)dx = 1\)，得：

\(\int_{-\infty}^{+\infty} f(x)dx = \int_{-\infty}^{0} 0dx + \int_{0}^{1} axdx + \int_{1}^{+\infty} 0dx = 1\)

$\because \ ax的一个原函数为 \frac{a}{2} x^2 $

即\(\int_{0}^{1} ax dx = \frac{a}{2} x^2 |_{0}^{1} = \frac{a}{2} 1^2 - \frac{a}{2} 0^2 = \frac{a}{2} = 1\)

\(\therefore \ a = 2\)

(2) 当\(x \lt 0\)时，\(F(x) = \int_{-\infty}^{x} f(t)dt = 0, \ \ (t \in x)\)

当\(0 \le x \le 1\)时，\(F(x) = \int_{-\infty}^{x} f(t)dt = \int_{-\infty}^{0} 0dt + \int_{0}^{x} atdt = \int_{0}^{x} 2tdt = x^2 |_{0}^{x} = x^2\)

当\(x \gt 1\)时，\(F(x) = \int_{-\infty}^{x} f(t)dt = \int_{-\infty}^{0} 0dt + \int_{0}^{1} atdt + \int_{1}^{x} 0dt = \int_{0}^{1} 2tdt = t^2 | _{0}^{1} = 1\)

这里教材上的积分下限为\(+\infty\)是错误的！！！

即\(X\)的分布函数为：

\[F(x)= \begin{cases} 0, & x \lt 0 \\ x^2, & 0 \le x \le 1 \\ 1, & x \gt 1 \end{cases} \]

(3) \(P\{|X| \le \frac{1}{2}\} = P\{-\frac{1}{2} \le X \le \frac{1}{2}\} = F(\frac{1}{2}) - F(-\frac{1}{2}) = \frac{1}{4} - 0 = \frac{1}{4}\)

或者\(P\{|X| \le \frac{1}{2}\} = \int_{-\frac{1}{2}}^{\frac{1}{2}} f(x)dx = \int_{-\frac{1}{2}}^{0} f(x)dx + \int_{0}^{\frac{1}{2}} f(x)dx = \int_{-\frac{1}{2}}^{0} 0dx + \int_{0}^{\frac{1}{2}} axdx = \int_{0}^{\frac{1}{2}} 2xdx = x^2 |_{0}^{\frac{1}{2}} = \frac{1}{4}\)

例2：设随机变量\(X\)的概率密度为：

\[f(x)= \begin{cases} x, & 0 \le x \lt 1 \\ 2-x, & 1 \le x \lt 2 \\ 0, & 其他 \end{cases} \]

求\(X\)的分布函数\(F(x)\)。

解：当\(x \lt 0\)时，\(F(x) = \int_{-\infty}^{x} f(t)dt = \int_{-\infty}^{0} 0dt = 0,\ \ t \in (x \lt 0, 即其他)\)

当\(0 \le x \lt 1\)时，\(F(x) = \int_{-\infty}^{x} f(t)dt= \int_{-\infty}^{0} 0dt + \int_{0}^{x} tdt = \int_{0}^{x} tdt = \frac{t^2}{2} | _{0}^{x} = \frac{x^2}{2}\)

当\(1 \le x \lt 2\)时，\(F(x) = \int_{-\infty}^{x} f(t)dt = \int_{-\infty}^{0} 0dt + \int_{0}^{1} tdt + \int_{1}^{x} (2-t)dt = \frac{t^2}{2}|_{0}^{1} + (2t-\frac{1}{2} t^2)|_{1}^{x} = -\frac{1}{2} x^2 + 2x + 1\)

当\(x \ge 2\)时，\(F(x) = \int_{-\infty}^{x} f(x)dx = \int_{-\infty}^{0} 0dt + \int_{0}^{1} tdt + \int_{1}^{2} (2-t)dt + \int_{2}^{x} 0dt = 0 + \frac{t^2}{2}|_{0}^{1} + (2t -\frac{1}{2} t^2) | _{1}^{2} + 0 = 0 + \frac{1}{2} + \frac{1}{2} + 0 = 1\)

即\(X\)的分布函数为：

\[F(x)= \begin{cases} 0, & x \lt 0 \\ \frac{x^2}{2}, & 0 \le x \lt 1 \\ -\frac{1}{2}x^2 + 2x + 1, & 1 \le x \lt 2 \\ 1, & x \ge 2 \end{cases} \]

再啰嗦一句：无论哪个区间\(F(x) = \int_{-\infty}^{x} f(t)dt\)；这是定义！！！！

例3：设连续随机变量\(X\)的分布函数为：

\[F(x) = \begin{cases} 0, & x \le 0 \\ x^2, & 0 \lt x \lt 1 \\ 1, & x \ge 1 \end{cases} \]

求：(1) \(X\)的概率密度\(f(x)\)； (2) \(X\)落入\((0.3,0.7)\)的概率密度。

解：(1) 根据分布函数与概率密度函数的关系知：

\[f(x) = F'(x) = \begin{cases} 2x, & 0 \lt x \lt 1 \\ 0, & 其他 \end{cases} \]

(2) 有两种解法：

\(P\{0.3 \lt X \lt 0.7\} = F(0.7) - F(0.3) = 0.7^2 - 0.3^2 = 0.4\)

或者：

\(P\{0.3 \lt X \lt 0.7\} = \int_{0.3}^{0.7} f(x)dx = \int_{0.3}^{0.7} 2xdx = x^2|_{0.3}^{0.7} = 0.4\)

\(\bigstar \bigstar \bigstar \bigstar \bigstar\)例4：设某型号电子元件的寿命\(X\)(单位：h)具有以下概率密度：

\[f(x) = \begin{cases} \frac{1000}{x^2}, & x \ge 1000 \\ 0, & 其他 \end{cases} \]

现有以下批次的此种元件（元件工作相互独立），问：

(1) 任取一只元件，求其寿命大于1500h的概率？

(2) 任取4只元件，其中恰好有2只元件的寿命大于1500h的概率？

(3) 任取4只元件，其中至少有1只元件的寿命大于1500h的概率？

解：(1) \(P\{X \gt 1500\} = \int_{1500}^{+\infty} \frac{1000}{x^2} dx = (-\frac{1000}{x})|_{1500}^{+\infty} = \frac{2}{3}\)

(2) 各元件工作独立，可以看作是进行4重伯努利试验，令\(Y\)表示"4个元件中寿命大于1500h的元件个数"，则\(Y \sim B(4, \frac{2}{3})\)；所有概率\(P\{Y = 2\} = C_4^2 (\frac{2}{3})^2 (\frac{1}{3})^2 = \frac{8}{27}\)

(3) 所求概率为\(P\{Y \ge 1\} = 1 - P\{Y = 0\} = 1 - C_4^0 (\frac{2}{3})^0 (\frac{1}{3})^4 = \frac{80}{81}\)

3.2 均匀分布与指数分布

最常用的连续型概率分布有：均匀分布、指数分布和正态分布。

定义9：若随机变量\(X\)的概率密度为：

\[f(x) = \begin{cases} \frac{1}{b-a}, & a \le x \le b \\ 0, & 其他 \end{cases} \]

则称\(X\)服从区间\([a,b]\)上的均匀分布，简记：\(X \sim U(a,b)\)。

容易求得分布函数：

\[F(x) = \begin{cases} 0, & x \lt a \\ \frac{x-a}{b-a}, & a \le x \le b \\ 1, & x \gt b \end{cases} \]

我这里还是补充下证明过程：

当\(x \lt a\)时；\(F(x) = \int_{-\infty}^{x} f(t)dt = 0|_{-\infty}^{x} = 0\) ；

当\(a \le x \le b\)时；\(F(x) = \int_{-\infty}^{x} f(t)dt = \int_{-\infty}^{a} 0dt + \int_{a}^{x} (\frac{1}{b-a})dt = 0|_{-\infty}^{a} + \frac{1}{b-a} t|_{a}^{x} = \frac{x}{b-a} - \frac{a}{b-a} = \frac{x-1}{b-a}\)

当\(x \gt b\)时；\(F(x) = \int_{-\infty}^{x}f(t)dt = \int_{-\infty}^{a} 0dt + \int_{a}^{b} (\frac{1}{b-a})dt + \int_{b}^{x} 0dt = (\frac{1}{b-a} t)|_{a}^{b} = 1\)

均匀分布的概率密度\(f(x)\)与分布函数\(F(x)\)的图像如下：

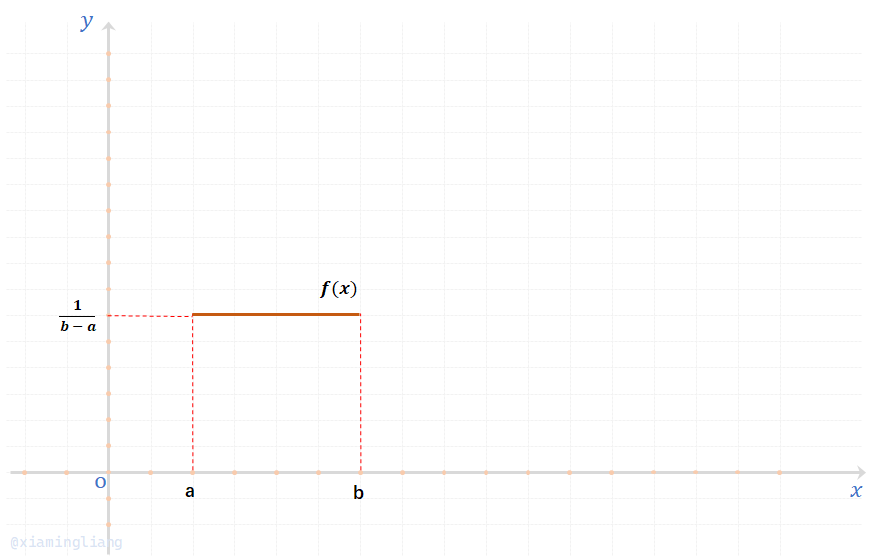
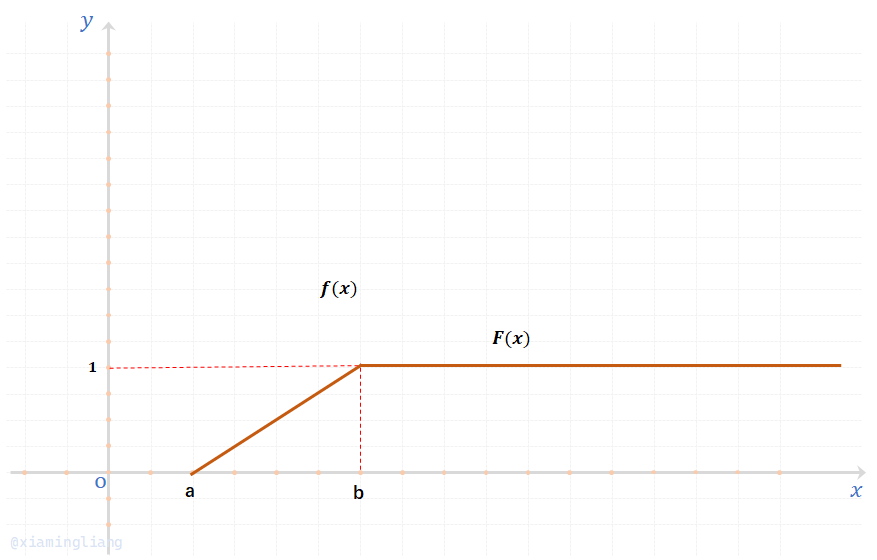
均匀分布的概率计算中有一个概率公式： \(\bigstar \bigstar \bigstar \bigstar \bigstar\)

设\(X \sim U(a,b),\ \ a \le c \lt d \le b\)即\([c,d] \subset [a,b]\)，则：\(P\{c \le X \le d\} = \frac{d-c}{b-a}\)。

使用这个公式计算均匀分布概率很方便，例如\(X \sim U(0,3)\)则\(P\{1 \le X \le 2\} = \frac{2-1}{3-0} = \frac{1}{3}\)

均匀分布可能是实际问题中最常见的了。

\(\bigstar \bigstar \bigstar \bigstar \bigstar\)

例5：公共汽车站每个5分钟有一辆车通过，乘客再5分钟内任一时刻到达车站是等可能的，求乘客候车时间在1-3分钟内的概率。

解：设\(X\)表示乘客的候车时间；则\(X \sim U(0,5)\)，其概率密度为：

\[f(x) = \begin{cases} \frac{1}{5}, & 0 \le x \le 5\\ 0, & 其他 \end{cases} \]

所求概率为：\(P\{1 \le x \le 3\} = \frac{3-1}{5-0} = \frac{2}{3}\)

定义10：若随机变量\(X\)的概率密度为：

\[f(x) = \begin{cases} \lambda e^{-\lambda x}, & x \gt 0 \\ 0, & x \le 0 \end{cases} \]

其中\(\lambda \gt 0\)是常数，则称\(X\)服从参数为\(\lambda\)的指数分布；简记：\(X \sim E(\lambda)\)；其分布函数为：

\[F(x) = \begin{cases} 1 - e^{-\lambda x}, & x \gt 0 \\ 0, & x \le 0 \end{cases} \]

\(f(x)\)与\(F(x)\)的图像为：

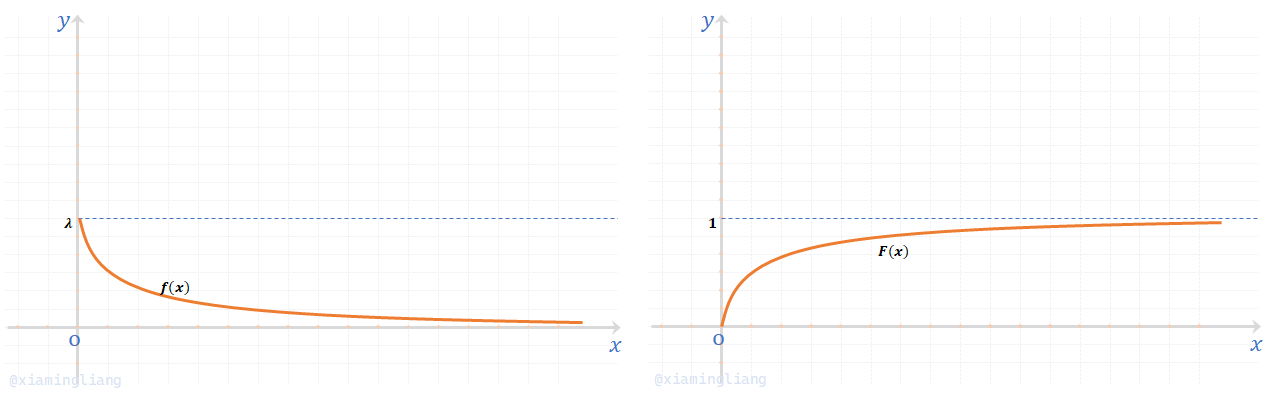
指数分布常用作各种"寿命"相关的分布，有广泛的应用。

例6：设\(X\)服从\(\lambda = 1\)的指数分布，求\(P\{X \gt 1\}\)。

解：\(X\)的概率密度为为：

\[f(x) = \begin{cases} e^{-x}, & x \gt 0 \\ 0, & x \le 0 \end{cases} \]

方法一：\(P\{X \gt 1\} = \int_{1}^{+\infty}f(t)dt\)；因为\(x \gt 0时，fx() = e^{-x}\)，因此：

\(P\{X \gt 1\} = \int_{1}^{+\infty}f(t)dt = \int_{1}^{+\infty} e^{-t}dt = -e^{-t} | _{1}^{+\infty} = e^{-1}\)。

方法二：\(P\{X \gt 1\} = 1 - P\{X \le 1\}\)；根据定义7：分布函数的定义得

\(P\{X \gt 1\} = 1 - P\{X \le 1\} = 1 - F(1) = 1 - [ \int_{-\infty}^{0}f(t)dt + \int_{0}^{1}f(t)dt] = 1 - [0 + (-e^{-t}) | _{0}^{1}] = 1 - (-e^{-1} - (-e^{}-0)) = e^{-1}\)

特别地啰嗦下：

方法一直接通过积分计算 概率密度与区间长度乘积的积分，积分上下限就根据\(X\)的取值范围即可。

方法二，辗转通过 概率函数的方法，再通过概率概率函数的性质来计算，那么积分就必须从\(-\infty\)积到边界线\(x=1\)。为什么是积到边界线而不是继续从边界线\(x=1\)继续积到\(x \to +\infty\)呢？因为，继续从边界线\(x=1\)继续积到\(x \to +\infty\)呢有概率密度计算概率函数\(F(x)\)的计算步骤，而这里已经确定\(x = 1\)了，因此不用再继续积下去。

关于积分上下限的说明

3.3 正态分布

定义11：若随机变量\(X\)的概率密度为：

\[f(x) = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\ \ \ \ ,\ \ \ \ -\infty \lt x \lt +\infty \]

其中\(\mu,\ \sigma^2\)为常数，\(-\infty \lt \mu \lt +\infty,\ \mu \gt 0\)，则称\(X\)服从参数为\(\mu,\ \sigma^2\)的正态分布，简记\(X \sim N(\mu, \sigma^2)\)。

\(f(x)\)的图形如下：

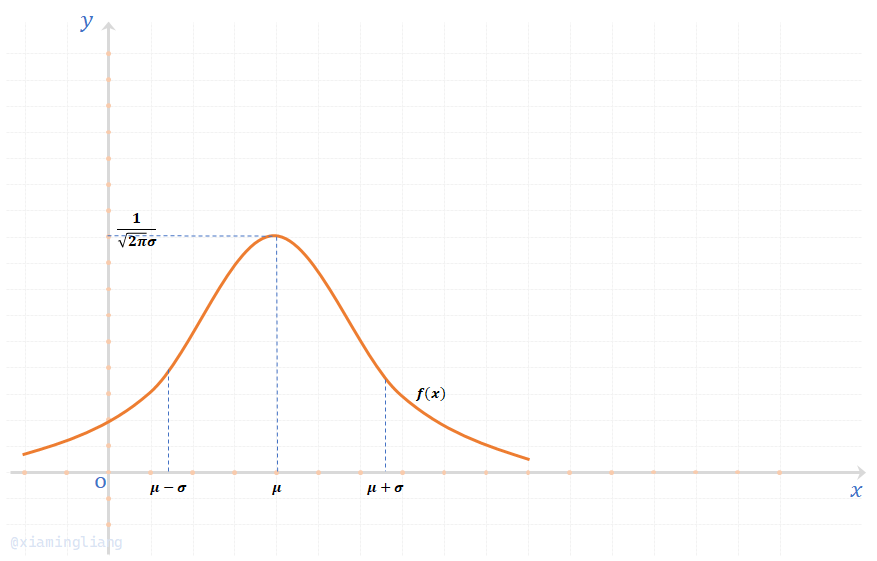
习惯上，称服从正态分布的随机变量为正态随机变量；又称正态分布的概率密度曲线为正态分布曲线，它有以下性质：

(1) 曲线关于之直线\(x = \mu\)对称，这表明对于任何\(h \gt 0\)，都有\(P\{\mu-h \lt X \lt \mu\} = P\{\mu \lt X \lt \mu + h\}\)。

(2) 当\(x = \mu\)时，取最大值\(f(\mu) = \frac{1}{\sqrt{2\pi} \sigma}\)，在\(x = \mu \pm \sigma\)处曲线有拐点；曲线以\(x\)轴为渐近线。

(3) 当\(\sigma\)给定，\(\mu_1 \lt \mu_2\)时；

\(f_1(x) = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu_1)^2}{2\sigma^2}}\ \ \ \ ,\ \ \ \ f_2(x) = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu_2)^2}{2\sigma^2}}\)

其图像为：

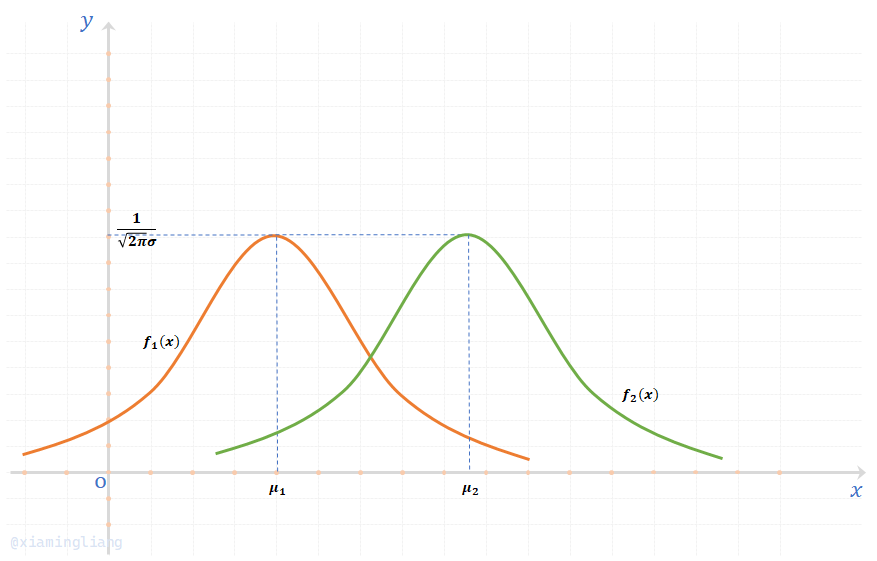
实际上，两条曲线可沿着\(x\)轴平移而得，不改变其形状，可见正态分布曲线的位置完全由\(\mu\)决定，\(\mu\)是正态分布的中心。

(4) 当\(\mu\)给定且\(\sigma_1 \lt \sigma_2\)时；

\(f_3(x) = \frac{1}{\sqrt{2\pi} \sigma_1} e^{-\frac{(x-\mu)^2}{2\sigma_1^2}}\ \ \ \ ,\ \ \ \ f_4(x) = \frac{1}{\sqrt{2\pi} \sigma_2} e^{-\frac{(x-\mu)^2}{2\sigma_2^2}}\)

其图像为：

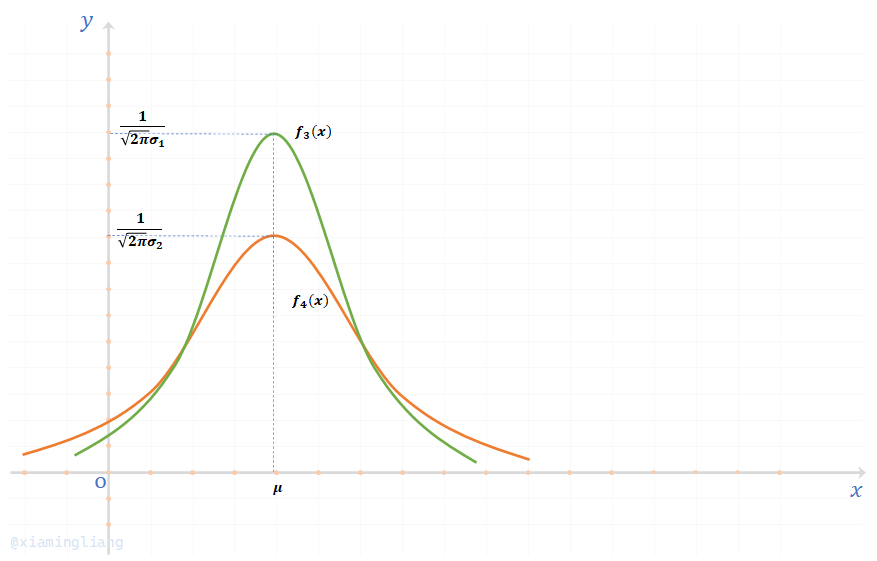
可见\(\sigma\)越小，图形越尖，\(\sigma\)越大，图形越平缓；正态分布曲线中\(\sigma\)的值刻画了正态随机变量取值的分散程度，\(\sigma\)越小，分散程度越小，\(\sigma\)越大，分散程度越大。

设\(X \sim N(\mu,\ \sigma^2)\)，则\(X\)的分布函数为：\(F(x) = \int_{-\infty}^{x} \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}dt\)；它的图形为：

特别地，当\(\mu = 0, \sigma = 1\)时，正态分布称为标准正态分布\(N(0,\ 1)\)。为了区别，标准正态分布的密度和分布函数分别记为\(\varphi(x),\ \varPhi(x)\)，即：

\(\varphi(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}},\ \ \ \ -\infty \lt x \lt +\infty\)

\(\varPhi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{-\frac{t^2}{2}}dt,\ \ \ \ -\infty \lt x \lt +\infty\)

其中，\(\varphi(x)\)的图像为：

显然，\(\varphi(x)\)是关于\(y\)轴对称的，且在\(x=0\)时取最大值\(\frac{1}{\sqrt{2\pi}}\)。

对于标准正态分布函数\(\varPhi(x)\)，它有下列性质：

(1) \(\varPhi(-x) = 1 - \varPhi(x)\) ；这根据前面的知识时显而易见的；

(2) \(\varPhi(0) = \frac{1}{2}\)；\(\varPhi(x)\)的值可以通过查询标准正态分布表获取；

下列公式揭示了一般正态分布函数\(F(x)\)与标准正态分布函数\(\varPhi(x)\)的关系：

(1) 设\(X \sim N(\mu,\ \sigma^2)\)，其分布函数为\(F(x)\)，则：\(F(x) = P\{X \le x\} = \varPhi(\frac{x-\mu}{\sigma})\)；证明过程：

因为：\(F(x) = \frac{1}{\sqrt{2\pi} \sigma} \int_{-\infty}^{x} e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt\)；作为代换，我们令\(u = \frac{t-\mu}{\sigma}\)，则\(\because u' = \frac{du}{dt} \ \ \therefore du = \frac{1}{\sigma}dt \ \ \therefore dt = \sigma du\)；

代换后：\(F(x) = \frac{1}{\sqrt{2\pi} \sigma} \int_{-\infty}^{\frac{x-\mu}{\sigma}} e^{-\frac{1}{2} u^2} \sigma du = \varPhi(\frac{x - \mu}{\sigma})\) # 注意，这里因为使用了代换量，积分上下界也要跟随变化！！

(2) \(P\{a \lt x \le b\} = P\{a \le x \lt b\} = P\{a \le x \le b\} = P\{a \lt x \lt b\} = F(b) - F(a) = \varPhi(\frac{b-\mu}{\sigma}) - \varPhi(\frac{a-\mu}{\sigma})\)

(3) \(P\{x \gt a\} = P\{ X \ge a\} = 1 - P\{ x \le a\} = 1 - F(a) = 1 - \varPhi(\frac{a - \mu}{\sigma})\)

例7：设\(X \sim N(0,1)\)，证明：对于任意的\(h \gt 0\)，有\(P\{|x| \le h\} = 2\varPhi(h) - 1\)。

证明：\(P\{|X| \le h\} = P\{-h \le X \le h\} = \varPhi(h) - \varPhi(-h) = \varPhi(h) - [1 - \varPhi(h)] = 2\varPhi(h) - 1\)

例8：设\(X \sim N(0,1)\)求：

(1) \(P\{X \lt 2.35\}\)

(2) \(P\{X \lt -3.03\}\)

(3) \(P\{|X| \lt 1.54\}\)

解：(1) \(P\{X \lt 2.35\} = \varPhi(2.35) = 0.9906\) （直接查表） # 找到行头为2.3，列头为5表格对应的值。

(2) \(P\{X \lt -3.03\} = \varPhi(-3.03) = 1 - \varPhi(3.03) = 1 - 0.9995 = 0.0005\) (查表)

(3) \(P\{|X| \lt 1.54\} = P\{-1.54 \lt X \lt 1.54\} = 2\varPhi(1.54) - 1 = 2 \times 0.9382 - 1 = 0.8764\)

例9：设\(X \sim N(1.5,4)\)求：

(1) \(P\{X \lt 3.5\}\)

(2) \(P\{1.5 \lt X \lt 3.5\}\)

(3) \(P\{|X| \ge 3\}\)

解：由题目知\(\mu = 1.5, \ \sigma = 2\)，记\(F(x)\)为\(X\)的分布函数：

(1) \(P\{X \lt 3.5\} = F(3.5) = \varPhi(\frac{x-\mu}{\sigma}) = \varPhi(\frac{3.5 - 1.5}{2}) = \varPhi(1) = 0.8413\)

(2) \(P\{1.5 \lt X \lt 3.5\} = F(3.5) - F(1.5) = F(1) - F(0) = 0.8413 - 0.5 = 0.3413\)

(3) $P{X \ge 3} = P{ X \le -3} + P{X \ge 3} = F(-3) + (1 - F(3)) $

\(= \varPhi(\frac{-3-1.5}{2}) + 1 - \varPhi(\frac{3-1.5}{2}) = \varPhi(-2.25) - \varPhi(0.75) + 1 = 1 - \varPhi(2.25) + 1 - varPhi(0.75) = 1-0.9878 + 1-0.7734 = 0.2388\)

\(\bigstar \bigstar \bigstar\)易错点提醒：\(F(-x)\)不一定等于\(1 - F(3)\)；只有在标准正态分布下\(\varPhi(-x) = 1-\varPhi(x)\)才成立！！！

同时，也可以利用\(P\{|X| \ge 3\} = 1 - P\{|X| \lt 3\} = 1 - P\{-3 \lt X \lt 3\}\)来计算！

例10：设\(X \sim N(\mu, \sigma^2)\)求\(X\)落在区间\([\mu -k\sigma, \mu +k\sigma]\)的概率，其中\(k=1,2,...\)

解：\(P\{\mu-k\sigma \le X \mu+k\sigma\} = F(\mu+k\sigma) - F(\mu-k\sigma) = \varPhi(\frac{(\mu + k\sigma)-\mu}{\sigma}) - \varPhi(\frac{(\mu - k\sigma)-\mu}{\sigma}) = \varPhi(k) - \varPhi(-k) = 2\varPhi(k) - 1\) ；则：

\(k=1;\ \ P\{\mu-\sigma \le X \le \mu+\sigma\} = 2\varPhi(1) - 1 = 0.6826\)

\(k=2;\ \ P\{\mu-2\sigma \le X \le \mu+2\sigma\} = 2\varPhi(2) - 1 = 0.9544\)

\(k=3;\ \ P\{\mu-3\sigma \le X \le \mu+3\sigma\} = 2\varPhi(3) - 1 = 0.9973\)

\(\bigstar \bigstar \bigstar\)由此可以看出：尽管正态随机变量取值范围为\((-\infty,+\infty)\)，但他的值落在\([\mu-3\sigma,\mu+3\sigma]\)的概率为\(0.9973\)，很接近\(100\%\)这个性质被称为正态分布的\(3\sigma\)规则。

大家应该都听过六西格玛质量管理模式，实际上也与此有关，大家有兴趣可以算算\(6\sigma ：[\mu-3\sigma,\mu+3\sigma]\)的概率。

定义12：设\(X \sim N(0,1)\)，若\(\mu_{\alpha}\)满足条件：\(P\{X \gt \mu_{\alpha}\} = \alpha, \ \ 0 \lt \alpha \lt 1\)；则称点\(\mu_{\alpha}\)为标准正态分布的上侧\(\alpha\)分位数，简称\(\alpha\)分位数。见图：

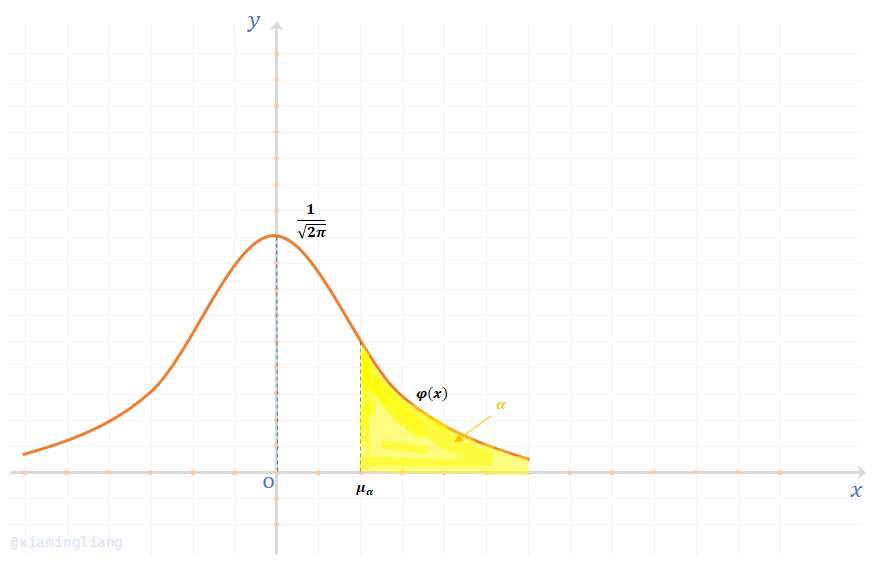
常见的上侧分位数：

\(\mu_{0.1} = 1.282,\ \ \ \ \mu_{0.05} = 1.645,\ \ \ \ \mu_0.025 = 1.960\)

\(\mu_{0.01} = 2.326,\ \ \ \ \mu_{0.005} = 2.567\)

\(\mu_{0.0001} = 3.090\)

4 随机变量函数的概率分布

4.1 离散型随机变量函数的概率分布

有时候我们所关心的随机变量不能直接测量得到，而他确是某个能直接测量的随机变量的函数。（可以某个简单函数的符合函数，大概就是这么个意思）

例如：我们能测量圆的直径\(X\)，而关心的却是其面接\(Y = \pi (\frac{X}{2})^2 = \frac{\pi}{4} X^2\)；这里随机变量\(Y\)就是随机变量\(X\)的函数。

设\(g(x)\)是一个给定的连续函数，称\(Y=g(X)\)为随机变量\(X\)的一个函数，\(Y\)也是一个随机变量；当\(X\)取值\(x\)时，\(Y\)取值为\(Y=g(x)\)。

接下来我们将讨论如何由已知的随机变量\(X\)的概率分布去求函数\(Y = g(X)\)的概率分布。

首先，讨论\(X\)为离散型随机变量，设其分布律为：

X	\(x_1\)	\(x_2\)	...	\(x_k\)	...
P	\(p_1\)	\(p_2\)	...	\(p_k\)	...

由于\(X\)的取值可能为\(x_1,\ x_2,\ ...,\ x_k,\ ...\)；所以\(Y\)的可能取值为\(g(x_1),\ g(x_2),\ ...,\ g(x_k),\ ...\)；可见\(Y\)只取有限多个或者可列的无限多个值，故\(Y\)也是一个离散型随机变量。

注意：\(g(x_1),\ g(x_2),\ ...,\ g(x_k),\ ...\)之间可能存在相等的情况。

我们关注的是如何求\(Y\)的分布律，先看一个例子：

例1：设随机变量\(X\)的分布律为：

X	-1	0	1	2
P	0.2	0.1	0.3	0.4

求：（1）\(Y=X^3\)的分布律； （2）\(Z = X^2\)的分布律。

解：（1）\(Y\)可能的取值有：\(-1,\ 0,\ 1,\ 8\)；且由于：

\(P\{Y = -1\} = P\{X^3 = -1\} = P\{X = -1\} = 0.2\)

\(P\{Y = 0\} = P\{X^3 = 0\} = P\{X = 0\} = 0.1\)

\(P\{Y = 1\} = P\{X^3 = 1\} = P\{X = 1\} = 0.3\)

\(P\{Y = 8\} = P\{X^3 = 8\} = P\{X = 2\} = 0.4\)

从而，\(Y\)的分布律为：

X	-1	0	1	8
P	0.2	0.1	0.3	0.4

（2）\(Z\)可能的取值为：\(0，1，4\)；且由于：

\(P\{Z = 0\} = P\{X^2 = 0\} = P\{X=0\} = 0.1\)

\(P\{Z = 1\} = P\{X^2 = 1\} = P\{X=-1\} +P\{X=1\} = 0.2+0.3 = 0.5\)

\(P\{Z = 4\} = P\{X^2 = 2\} = P\{X=2\} = 0.4\) # \(X=-2\)的情况对于\(X\)来说概率是\(0\)

从而，\(Z\)的分布律为：

X	0	1	4
P	0.1	0.5	0.4

\(\bigstar \bigstar \bigstar\)从此例可以看出，\(g(x_1),\ g(x_2),\ ...,\ g(x_k),...\)中的值可能互不相等，也可能有相等的情况，对于\(g(x_k)\)相等的那些\(x_k\)所对应的概率应改相加作为\(g(x_k)\)的概率。

例2：设\(X \sim B(3,\ 0.4)\)，令\(Y = \frac{X(3-X)}{2}\)，求\(P\{Y=1\}\)。

解：由题目知：

\[P\{Y = 1\} &= & P\{\frac{X(3-X)}{2} = 1\} &\\ & = & P\{X = 1\} + P\{X = 2\} &\\ & = & C_3^1(0.4)^1(0.6)^2 + C_3^2(0.4)^2(0.6)^1 &\\ & = & 0.72 &\\ \]

4.2 连续型随机变量函数的概率分布

设\(X\)为连续型随机变量，其概率密度为\(f(x)\)，要求\(Y=g(X)\)的概率密度\(f_Y(y)\)，我们可以利用如下定理的结论。

定理1：设\(X\)为连续型随机变量，其概率密度为\(f_X(x)\)，设\(g(x)\)是一个严格单调可导的函数，其值域为\((\alpha,\ \beta)\)且\(g'(x) \ne 0\)；记\(x=h(y)\)为\(y=g(x)\)的反函数，则\(Y=g(X)\)的概率密度为：

\[f_Y(y) = \begin{cases} f_X(h(y))|h'(y)|,\ \ \ \ & \alpha \lt y \lt \beta \\ 0,\ \ \ \ & 其他 \end{cases} \]

特别地，当\(\alpha =-\infty,\ \beta = +\infty\)时：

\(f_Y(y) = f_X(h(y))|h'(y)|,\ \ \ \ \ -\infty \lt y \lt +\infty\) 。

例3：设连续性随机变量\(X\)的概率密度为\(f_X(x)\)，令\(Y = aX + b\)，其中\(a,\ b\)为常数\(a \ne 0\)，求\(Y\)的概率密度。

解：由题目知，设：\(y = g(x) = ax+b\)则：

\(x = h(y) = \frac{y-b}{a},\ \ h'(y) = \frac{1}{a}\)

\(f_Y(y) = f_X(h(y)) \cdot |h'(y)| = f_X(\frac{y-b}{a}) \cdot |\frac{1}{a}|\)

例4：\(X \sim N(\mu, \sigma^2)\)求：（1）\(Y = \frac{X-\mu}{\sigma}\)的概率密度；（2）\(Y = aX+b\)的概率密度。

解：由题目知\(X\)的概率密度为：\(f_X(x) = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)

（1）\(Y = \frac{X - \mu}{\sigma} = \frac{1}{a}X + (-\frac{\mu}{a})\)

\(x = h(y) = \sigma y+\mu,\ \ h'(y) = \sigma\)

\(f_Y(y) = f_X(h(y)) \cdot |h'(y)| = f_X(\sigma y + \mu) \cdot \sigma = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(\sigma y + \mu -\mu)^2}{2\sigma^2}} \cdot \sigma = \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}}\)

即：\(Y \sim N(0,\ 1)\)。

（2）由例3中的结论\(f_Y(y) = f_X(\frac{y-b}{a}) \cdot |\frac{1}{a}| = \frac{1}{|a|} \cdot \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(\frac{y-b}{a}-\mu)^2}{2\sigma^2}} = \frac{1}{\sqrt{2\pi} \sigma|a|} e^{-\frac{(y-b-a\mu)^2}{2(\sigma a)^2}}\)

即：\(Y \sim N(b+a\mu, a^2\sigma^2)\)

$\bigstar \bigstar \bigstar \(本示例说明了两个重要的结论：当\)X \sim N(\mu, \sigma^2)\(时\)Y = \frac{X-\mu}{\sigma} \sim N(0,\ 1)\(且随机变量\)\frac{X-\mu}{\sigma}\(称为\)X\(的标准化。另外，正态随机变量的线性变换\)Y=aX+b\(仍旧是正态随机变量，即\)aX+b \sim N(b+a\mu,\ a^2\sigma2)$。

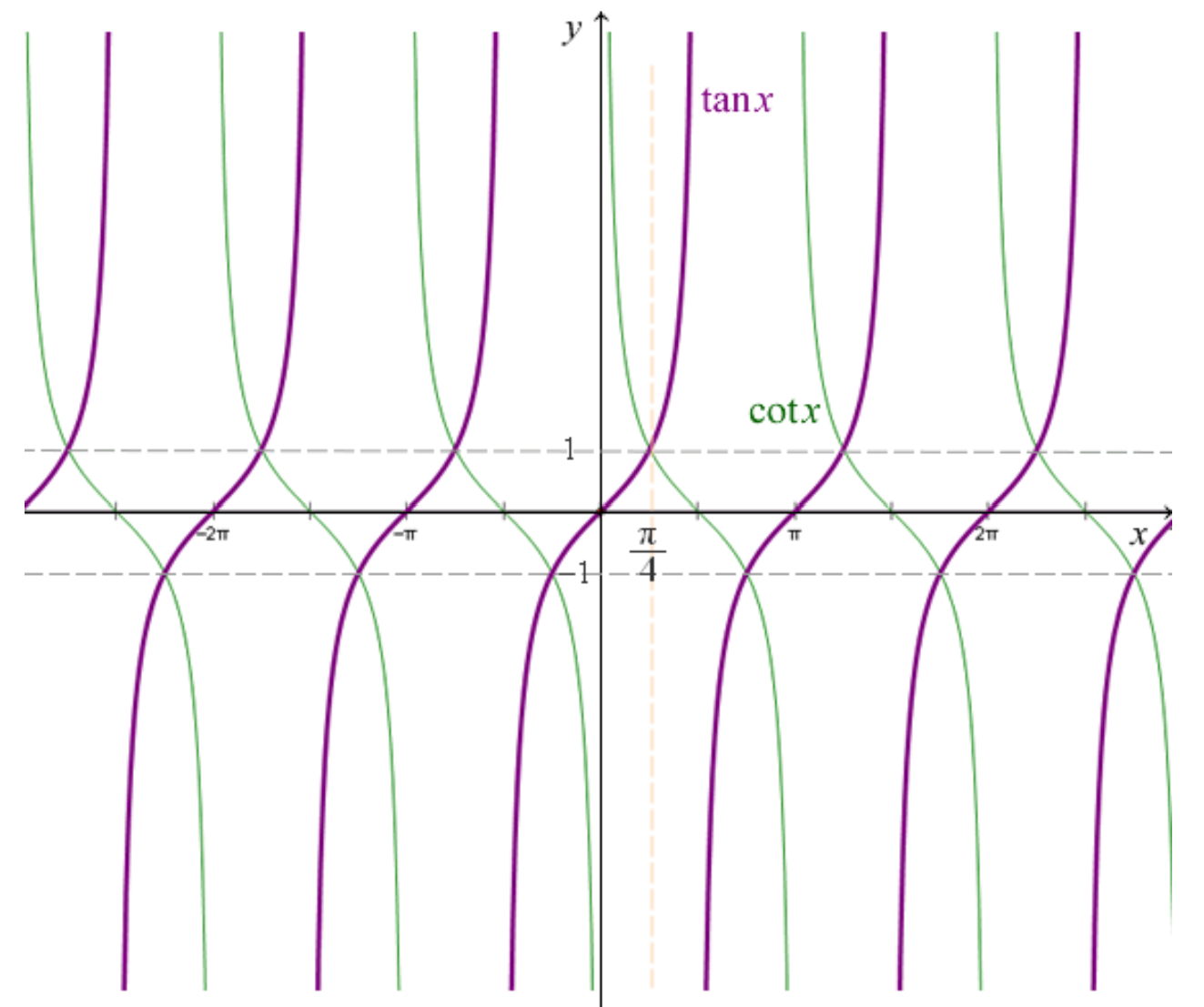
例5：设\(X \sim U(-\frac{\pi}{2},\ \frac{\pi}{2})\)，令\(Y=\tan{X}\)，求\(Y\)的概率密度\(f_Y(y)\)。

解：由题目知，\(X\)服从均匀分布，其概率密度为：

\[f_X(x) = \begin{cases} \frac{1}{\pi},\ \ & -\frac{\pi}{2} \le x \le \frac{\pi}{2}\\ 0,\ \ &其他 \end{cases} \]

令\(y = g(x) = \tan{x}\)，其值域为\((-\infty, +\infty)\)；

其反函数：\(x = h(y) = \arctan{y}\)；反函数的倒数：\(h'(y) = \frac{1}{1+y^2}\)

因此：\(f_Y(y) = f_X(h(y)) \cdot |h'(y)|,\ \ \ \ \arctan{y} \in (-\frac{\pi}{2},\ \frac{\pi}{2})\)

\(f_X(h(y)) = \frac{1}{\pi}; 又因：|\frac{1}{1+y^2}| = \frac{1}{1+y^2}\)

\(\therefore f_Y(y) = \frac{1}{\pi} \cdot \frac{1}{1+y^2}\)

这一概率分布也称为柯西(cauthy)分布。

\(\tan{x}、\cot{x}\)的图像：

①\((\sin{x})'=\cos{x}\)；即正弦的导数是余弦.

②\((\cos{x})'=-\sin{x}\)；即余弦的导数是正弦的相反数.

③\((\tan{x})'=(\sec{x})^2\)；即正切的导数是正割的平方.

④\((\cot{x})'=-(\csc{x})^2\)；即余切的导数是余割平方的相反数.

⑤\((\sec{x})'=\sec{x}\tan{x}\)；即正割的导数是正割和正切的积.

⑥\((\csc{x})'=-\csc{x}\cot{x}\)；即余割的导数是余割和余切的积的相反数.

⑦\((\arcsin{x})'=\frac{1}{\sqrt{(1-x^2)}}\)

⑧\((\arccos{x})'=-\frac{1}{\sqrt{(1-x^2)}}\)

⑨\((\arctan{x})'=\frac{1}{(1+x^2)}\)

⑩\((\arccot{x})'=-\frac{1}{(1+x^2)}\)

例6：设\(X \sim N(\mu,\sigma^2)\)，求\(Y = e^X\)的概率分布\(f_Y(y)\)。

解：令\(y = g(x) = e^x\)；其值域为\((0, +\infty)\)

其反函数为：\(x = h(y) = \ln{y}\)；反函数的倒数为：\(h'(y) = \frac{1}{y}\)则：

\[f_Y(y)& = \begin{cases} f_X(h(y)) \cdot |h'(y)|, \ \ & y \gt 0\\ 0, \ \ & y \le 0 \end{cases} \\ &=\begin{cases} \frac{1}{\sqrt{2\pi} \sigma y} e^{-\frac{(\ln{y} - \mu)^2}{2\sigma^2}},\ \ \ \ \ \ \ & y \gt 0 \\ 0,\ \ & y \le 0 \end{cases} \]

此分布为"对数正态分布"。

以上例子中使用公式求解，因此也叫"公式"法；注意：公式要求\(y = g(x)\)为单调函数，若不是单调函数则不能使用公式法求解。

例7：设随机变量\(X\)的概率密度为：

\[f_X(x)= \begin{cases} \frac{x}{8},\ \ &0 \lt x \lt 4 \\ 0,\ &其他 \end{cases} \]

求：\(Y = 2X + 8\)的概率密度。

解：设\(Y\)的分布函数为\(F_Y(y)\)，则：

\(F_Y(y) = P\{Y \le y\} = P\{2X + 8 \le Y\} = P\{X \le \frac{y-8}{2}\} = F_X(\frac{y-8}{2})\) 其中\(F_X(x)\)是\(X\)的分布函数；故：

\[f_Y(y) = F'_Y(y) = [F_X(\frac{y-8}{2})]' = F'_X(\frac{y-8}{2}) \cdot \frac{1}{2} = f_X(\frac{y-8}{2}) &= \begin{cases} \frac{1}{8} \cdot (\frac{y-8}{2} \cdot \frac{1}{2}) ,\ \ &0 \lt \frac{y-8}{2} \lt 4 \\ 0,\ & 其他\\ \end{cases}\\ &= \begin{cases} \frac{y-8}{32} , &8 \lt y \lt 16 \#课本里此处错误 \\ 0,\ & 其他 \end{cases} \]

注意：这里的\(F'_Y(y) = [F_X(\frac{y-8}{2})]' = F'_X(\frac{y-8}{2}) \cdot (\frac{y-8}{2})'= F'_X(\frac{y-8}{2}) \cdot \frac{1}{2}\)是复合函数求导的方法！！

这种解法叫"直接变换法"，它可以适用于非单调性随机变量的情况，但本例中\(Y = 2X+8\)是单调函数（切线的斜率或者导数不会更改正负号的函数），因此即可以使用前面的"公式法"，也可以使用"直接变换法"。

例8：设\(X\)的概率密度为\(f_X(x)\)，求\(Y = X^2\)的概率密度\(f_Y(y)\)，特别地，当\(X \sim N(0,1)\)时，求\(Y = X^2\)的概率密度。

明显\(Y=X^2\)不是单调函数了。

解：当\(y \le 0\)时，\(Y\)的分布函数为：\(F_Y(y) = P\{Y \le y\} = P\{X^2 \le y\} = 0\) #这是常识判断的，因为不存在实数的平方是负数的情况。

因此：\(f_Y(y) = 0\)

当\(y \gt 0\)时，\(Y\)的分布函数为：\(F_Y(y) = P\{Y \le y\} = P\{X^2 \le y\} = P\{-\sqrt{y} \le x \le \sqrt{y}\} = F_X(\sqrt{y}) - F_X(-\sqrt{y})\)

其中，\(F_X(x)\)时\(X\)的分布函数，则：

\(f_Y(y) = F'_Y(y) = (F_X(\sqrt{y}) - F_X(-\sqrt{y}))' = \frac{1}{2\sqrt{y}} \cdot F'_X(\sqrt{y}) + \frac{1}{2\sqrt{y}} \cdot F'_X(-\sqrt{y}) = \frac{1}{2\sqrt{y}} (f_X(\sqrt{y}) + f_X(-\sqrt{y}) )\) # 注意\(F\)和\(f\)的变化。

根据题目知：\(X \sim N(0,1)\)，则：\(f_X(x) = \frac{1}{\sqrt{2\pi}} e^{- \frac{x^2}{2}}\) 可得：

\(f_Y(y) = \frac{1}{2\sqrt{y}} (\frac{1}{\sqrt{2\pi}} e^{-\frac{y}{2}} + \frac{1}{\sqrt{2\pi}} e^{-\frac{y}{2}}) = \frac{1}{\sqrt{2\pi y}} e^{- \frac{y}{2}}\)

综上：

\[f_Y(y)= \begin{cases} \frac{1}{\sqrt{2\pi y}} e^{- \frac{y}{2}} , \ \ & y \gt 0\\ 0 , \ \ & 其他 \end{cases} \]

\(X \sim N(0,1)\)则\(Y = X^2\)为\(\chi^2\)分布，其自由度为\(1\)，记作：\(Y \sim \chi^2(1)\)。将在后面的章节详细讲解。