Burnside 引理
本文只讲一些 Burnside 引理 的应用,证明啥的不会,因为计算机科学家不需要证明。
一些抽象的定义非常不严谨,但是比较通俗易懂,大佬勿喷,因为初三 oier 不会群论。
内容
Burnside 引理主要用来解决对于一些变换,求本质不同方案数的问题。
对于这些变换,是有要求的,就是它们要形成一个“群”。因为群的定义比较抽象,你可以认为就是要求这些变换时封闭的。
以 洛谷 P4980 为例。这个题中的变换是旋转,转两下还是一种旋转。设变换方式组成的集合为 \(G\),那么对于任意 \(x, y \in G\),要满足 \(x \cdot y \in G\),就是先做 \(x\) 在做 \(y\) 的结果也在 \(G\) 里。类似的还有翻转,这个也是封闭的。
Burnside 引理:本质不同的方案数 $ = \frac{1}{|G|} \sum\limits_{x \in G} 在 x 下不变的方案数$ 。证明 CTJ 去吧。
还是以旋转为例,它的变换就是 \(n\) 种旋转(只是旋转角度不同)。那么旋转本质不同的方案数就是 \(\frac{1}{n}\sum\limits_{x = 0}^{n - 1} (顺时针)转 \ x \ 下不变的方案数\)(方向无所谓)。
举个例子,设 \(n = 4\),进行 \(4\) 染色。那么转 \(0\) 次不变的方案数是 \(4^4 = 256\)(每个点独立),转 \(1\) 次不变的方案数为 \(4^1 = 4\)(每个点的颜色都相同),转 \(2\) 次不变的方案数为 \(4^2 = 16\)(第一个颜色与第三个相同,第二个与第四个相同),转 \(3\) 次不变的就是 \(4^1 = 4\)(与转 \(1\) 次是等价的。)
不理解可以见下图(连线表示颜色要一样。)答案就是 \(\frac{1}{4}(256 + 4 + 16 + 4) = 70\)。
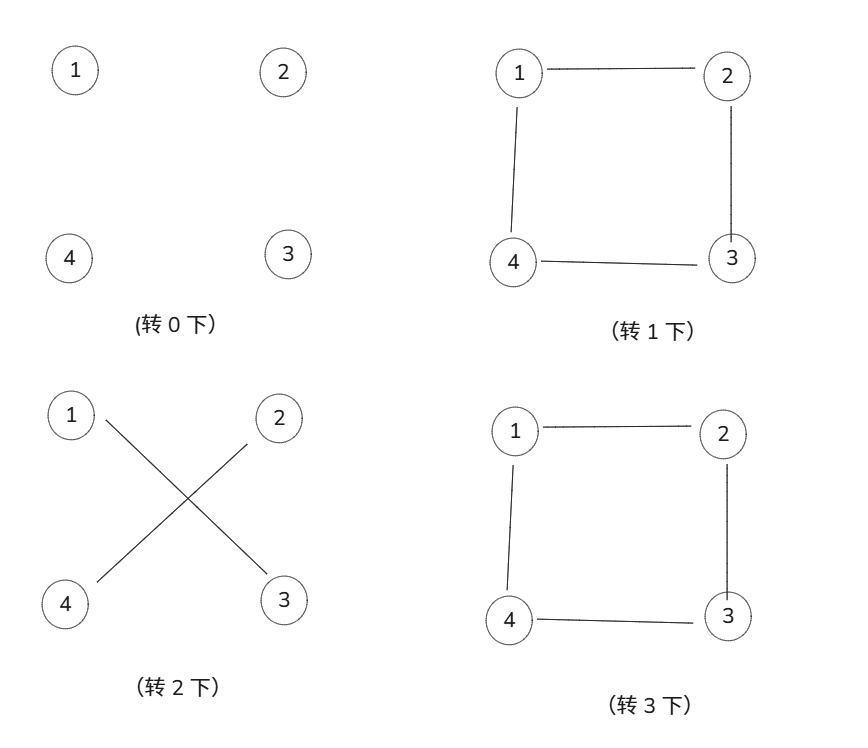
那么对于这个题,设转了 \(x\) 下,那么会形成 \(\gcd(x, n)\) 组,每组内的点颜色相同,那么答案就是
考虑优化,可以枚举 \(d = \mid n\),求有多少个 \(x\) 满足 \(\gcd(x, n) = d\),即 \(\gcd(\frac{n}{x}, \frac{n}{d}) = 1\)。又因为 \(1 \le x \le n\),则有 \(\varphi(\frac{n}{d})\) 个 \(x\) 满足要求,所以总方案数就是:
[MtOI2018] 魔力环 - 洛谷 P4916
有一个由 \(n\) 个珠子组成的环,每个珠子有黑白二色。一个环是美妙的当且仅当:
- 环上恰有 \(n\) 个珠子是黑色的,\(n - m\) 个珠子是白色的。
- 不会出现连续的 \(k + 1\) 个黑色珠子。
问有多少个本质不同的环是美妙的,两个环不同当且仅当不能通过旋转使一个环变成另一个。
\(n, k \le 10^5, m \le n\)
和上个题一样,还是求旋转 \(x\) 下后不变的方案数。实际上就是第 \(i\) 个珠子和第 \(i + \gcd(x, n)\) 个的颜色相同即可。也就是说整个环是由大小为 \(d\) 的串循环 \(\frac{n}{d}\) 次组成。
如果 \(m < n\),那么问题就可以转化为有多少个长度 \(d\) 的环是美妙的。(因为两个串拼接的黑色串也算)
要特判一下 \(n = m\) 的情况。
设这个环内有 \(p = m\frac{d}{n}\) 个黑色珠子,\(q = (n - m)\frac{d}{n}\) 个白色珠子(所以要求 \(n / d\) 是 \(m\) 的因子)。先把 \(q\) 个白色珠子放好,那么有 \(q\) 个空位,设每个空位有 \(x_i(1 \le i \le q)\) 个黑色珠子,那么要求:
- \(\sum x_i = p\)
- \(x_i \le k\)
这是一个经典问题,进行容斥,枚举有至少多少个 \(x_i > k\) 即可。不会的去看”硬币购物“。
还有一点,因为这个环实际上是一个大小为 \(d\) 的串,那么这样一个环其实对应了很多个串,需要枚举 \(x_1\),那么有 \(x_1 + 1\) 种方案断环为链,即一个串的开头可能有 \(0, 1, 2, \dots x_1\) 个黑色珠子,所以方案数还要乘 \(x_1 + 1\)。(可以理解为这个串循环移动得到的串实际上是本质相同的,所以一个环对应很多个串)
时间复杂度:
-
对于每个 \(d\),枚举 \(x_1\),\(O(k)\)
-
容斥时枚举有多少个 \(x_i > k\),\(O(\frac{p}{k})\)。
-
不妨设 \(t = \frac{n}{d}\),那么 \(t \mid \gcd(n, m)\),且对于每个 \(t\) 花费 \(O(p) = O(\frac{m}{t})\) 的时间,总时间复杂度:\(O(σ(\gcd(n, m)))\),\(σ\) 是约数和
[HNOI2008] Cards - 洛谷 P1446
有 \(n\) 张牌,\(m\) 种洗牌方式,每种洗牌方式给定序列 \(x\),表示第 \(i\) 位变为原本第 \(x_i\) 位的牌。
输入数据保证任意多次洗牌都可用这 \(m\) 种洗牌法中的一种代替,且对每种洗牌法,都存在一种洗牌法使得能回到原状态。
现在给 \(n\) 张牌进行染色,有三种颜色红蓝绿,要求出现 \(c_1\) 张红色,\(c_2\) 张蓝色,\(c_3\) 张绿牌。
问有多少种本质不同的染色方式。(通过洗牌不能使一种洗成另一种。)
\(\max\{c_1, c_2, c_3\} \le 20, m \le 60\)。
首先我们分析一下题目条件,什么叫做 “任意多次洗牌都可用这 \(m\) 种洗牌法中的一种代替”?不就是说这 \(m\) 种洗牌法可以形成一个群吗。
当然还有假设 \(x = \{1, 2, \dots , n\}\) 这种洗牌方式,因为不洗牌也是一种,而且洗回原样也是可以的。
那么就直接套 Burnside 引理 了,对于每种洗牌法,计算有多少种染色方式,在洗牌前后颜色是一样的。
我们将 \(x_i\) 向 \(i\) 连边,会形成若干个环,那么一个环内的牌颜色必须相同,直接进行背包 DP 即可。
时间复杂度:\(O(mn(maxc^2))\)。
[HNOI2009] 图的同构计数 - 洛谷 P4727
给定 \(n\),问有多少个在同构意义下,有 \(n\) 个节点的简单图。(最多 \(n(n - 1) / 2\) 条边)
A 图与 B 图被认为是同构的是指:A 图的顶点经过一定的重新标号以后,A 图的顶点集和边集要完全与 B 图一一对应。
\(n \le 60\)
相当于给每条边染一种颜色,两个题区别在于一个固定的两种颜色,一个给了 \(m\) 种颜色。
设 A 中的 \(i\) 号节点对应 B 中的 \(x_i\) 号节点,那么 \(x\) 就是一种变换,总共 \(n!\) 种变换就形成了一个群。
还是考虑 Burnside 引理,也就是说对于每种变换 \(x\),A 图变换为 B 图,有多少种染色方式满足对于任意 \((u, v)\),在 A 中的颜色和 B 中的相同。
对于变换 \(x\),还是会形成若干个环,我们把边分成环内的与环之间的进行考虑。
环内边
设环长为 \(k\),设 \(u, v\) 之间的距离为 \(d\)(算劣弧的边),也就是 \(d \le k / 2\),那么对于所有这样的 \((u, v)\),它们的颜色必须相同(同时位移)。所以总共有 \(\lfloor \frac{k}{2} \rfloor\) 个组边。
以 \(k = 5, 6\) 为例,相同颜色边表示这些边在同一组,颜色必须一致。不同组的没有要求。
\(k = 6\) 有 \(3\) 组, \(k = 5\) 有两组。
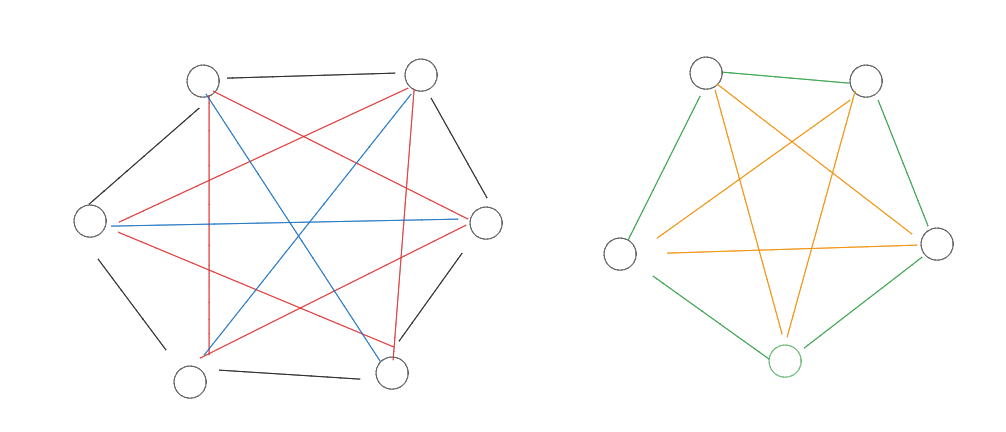
环间边
设两个环的环长为 \(l_1, l_2\),两个环都按顺时针依次编号,从 \(0\) 开始。设第一个环的节点 \(u\) 与第二个环的节点 \(v\) 连边 。那么 \(col(u, v) = col((u + 1) \% l1, (v + 1) \% l2)\)。
从 \((u, v)\) 开始往后跳,又调回了 \((u, v)\) 总共跳了 \(k\) 步,则 \(l1 | k, l2 | k\),所以 \(\text{lcm}(l1, l2) | k\)。所以这么跳就会形成 \(\gcd(l1, l2)\) 个环,每个环包含 \(\text{lcm}(l1, l2)\) 条边,也就是分成了 \(\gcd(l1, l2)\) 组。
自己画一下吧,比较丑。
于是设变换 \(x\) 形成 \(c\) 个环,大小依次为 \(a_1, a_2, \dots a_c\),那么有 \(m^{\sum\limits_{i = 1}^c \lfloor \frac{a_i}{2} \rfloor + \sum\limits_{i = 1}^c\sum\limits_{j = i + 1}^c \gcd(a_i, a_j)}\) 种染色方案。
但是总共 \(n!\) 种变换,显然是不可以直接枚举的。如何优化?
注意到答案之和环长有关,不妨设有 \(cnt_i\) 个环大小为 \(i\),那么答案就是:
那么这样有多少个 \(cnt\) 数组,答案其实就是 \(n\) 的无序拆分数 \(p(n)\),A296010 - OEIS,\(p(60) < 10^6\)
还有一个问题,\(cnt\) 数组对应多少个变换 \(x\)?自己推一推,这里报个答案:
预处理 gcd 与 \(m^p\),搜索 cnt,使用 \(O(K^2)\) 的复杂度计算,\(K\) 为 \(\sum\limits_{i = 1}^ n[cnt_i > 0]\)。加点搜索剪枝即可通过。
当然可以直接打表通过。
时间复杂度:\(O(可过)\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号