线性基进阶

本文介绍一些线性基的进阶套路、技巧，性质以及应用。

下文中的 \(W\) 为值域。

洛谷 P4869

给定 \(n\) 个数 \(a_1 \sim a_n\)，对于集合 \(S \sube \{1, 2, \dots, n\}\)，\(f(S) = XOR \{ a_x \}(x \in S)\)，对于所有的 \(S\)，对 \(f(S)\) 排序。

给定 \(x\)，求 \(x\) 在排序后的序列中第一次出现的位置。

\(n \le 10^5, W \le 10^9\)。

这个题主要是告诉我们线性基的一个性质。

设这个线性基内有 \(c\) 个元素，另外有 \(n - c\) 不在其中（自由元），那么共有 \(2^c\) 种不同的 \(f(S)\)，每种都出现 \(2^{n - c}\) 次。

证明是这样的，设这这 \(2^c\) 种 \(f(S)\) 形成集合 \(U\)，那些自由元中选出来的数的异或和为 \(v\)，对于每个 \(v\) 和每个 \(u \in U\) 来说，线性基中的元素都有唯一的方式凑出 \(v \oplus u\)，所以每种 \(u\) 都有 \(2^{n - c}\) 个。

所以只需要求出 \(x\) 在去重后的 \(f(S)\) 中的排名 \(rnk\)，答案就是 \((rnk - 1)2^{n - c} + 1\)。

怎么求比较简单，从高到低枚举线性基中的位置 \(i\)，保证异或出的数 \(now\) 高于 \(i\) 的位与 \(x\) 相同即可。

时间复杂度：\(O(n\log W)\)。

CF1100F

给定长度为 \(n\) 的序列 \(a\)，\(T\) 组询问，每组询问给定区间 \([l, r]\)，维护这个区间的线性基。

\(n \le 5 \times 10^5, W \le 10^6\)

区间线性基，难点在于线性基本身不支持删除。

一些暴力

一个暴力到极致的做法是进行回滚莫队，但显然爆了。

然后你想到了分块，进一步可以使用倍增，但是线性基合并是 \(O(\log^2 W)\)，时间复杂度来到 \(O((n + q) \log n \log^2 W)\)，无法接受。

接下来介绍一些比较可行的做法。

分治

虽然不是最优方式，但也是一种值得记录的思路。

对于一个分治中心 \(mid\)，设对应区间为 \([L, R]\)。对于左半边的每个 \(i\)，维护 \([i, mid]\) 的线性基，可以通过递推得到，右半边同理。

查询时合并两个线性基即可，时间复杂度：\(O(n \log^2 n + T \log^2 W)\)。

树上版本：[SCOI2016] 幸运数字 - 洛谷 P3292，使用点分治即可。

正解

可以发现，前面两种做法的瓶颈都在于线性基合并，而这玩意是无法优化的，所以我们要考虑避开它。

离线下来，考虑对于依次枚举 \(r\)， 计算 \(l\) 的答案。因为线性基和元素的加入顺序是没有关系的，而更靠后的元素显然可以对更多的 \(l\) 贡献，所以我们要维护一个最大编号的线性基，相当于是从后往前加入元素。

假设我们得到了一个对于 \([1, r]\) 的线性基 \(V_r\)，那么 \([l, r]\) 的线性基就是去掉里面 \(< l\) 的元素即可。

从 \([1, r]\) 转移到 \([1, r + 1]\)，首先把 \(a_{r + 1}\) 丢到线性基里。而 \([1, r]\) 中的元素只有在 \(V_r\) 才可能在 \(V_{r + 1}\)（其他的被单调队列了），那么尝试把 \(V_r\) 中的元素依次加入即可，时间复杂度：\(O(n \log^2 W + T \log W)\)。

---

继续优化，这次我们直接将 \(a_{r + 1}\) 硬塞到 \(V_r\)，得到 \(V_{r + 1}\)。按照线性基的加入方式，只需要找到 \(a_{r + 1}\) 的最高的 \(1\) 的位置即可。

如果这个位置是空的，直接放进去就行；否则，设在这里的是 \(a_x\)，应该把 \(a_{r + 1}\) 放到这个位置，令 \(a_x \leftarrow a_x \oplus a_{r + 1}\)，继续向下插入 \(a_x\)

于是我们就有了这样一个做法：设当前拿在手上的是 \(a_u\)（最初 \(u = r + 1\)），依次从高到低枚举每一位，如果 \(a_u\) 这一位是 \(1\)，做这样几种操作：

• 若这个位置是空的，把 \(a_u\) 放到这里，退出。
• 否则，设这个位置上的数是 \(a_x\)。（如果 \(u > x\)，就 swap(u, x)）然后 \(a_u \leftarrow a_u \oplus a_x\) 即可。

时间复杂度：\(O((n + T) \log W)\)。

struct Bases {
  int base[20], vis[20]; // 放在这个位置上的数，以及编号

  void Insert(int x, int id) {
    for (int i = 19; i >= 0; i--) {
      if ((x >> i) & 1) {
        if (!base[i]) { // 把 a[id] 放在这里。
          base[i] = x, vis[i] = id; break;
        }
        if (id > vis[i]) { // 交换
          swap(base[i], x), swap(vis[i], id);
        }
        x ^= base[i];
      }
    }
  }
}

黑暗爆炸 4184

有一个集合初始为空的集合 \(S\)，\(n\) 次操作，加入/删除一个数，维护每个时刻的线性基。

\(n \le 5 \times 10^5, W < 2^{31}\)

一个经典的做法是线段树分治，时间复杂度：\(O(n \log n \log W)\)。

这个和上面那个差不多，维护最大删除编号的线性基（就是对于每个元素，设其删除时间为 \(t_i\)，线性基里的元素 \(t_i\) 是最大的），加入一个元素时按上面的做即可。删除元素 \(u\) 时，本来可能有 \(a_v\) 来替代它，但是要替代它，必须满足 \(t_v > t_u\)（不然已经被删掉了），但是这有不符合 最大删除编号 这个原则，所以直接删掉即可。

时间复杂度：\(O(n \log W)\)。

顺便提一句，如果要维护连通性，也可以这么做，维护最大删除编号生成树即可，只不过应该要使用 LCT，但是还是省掉删除一条边，可能新加入一条的麻烦。

洛谷 P10778

给定一张 \(n\) 个点 \(m\) 条边的无向连通图，\(T\) 次查询，每次查询给定 \(k\) 条边，问删除这 \(k\) 条边后图是否连通？

强制在线。

\(n \le 10^5, m \le 5 \times 10^5, T \le 5\times 10^4, k \le 15\)。

离线直接线段树分治就做完了，可惜强制在线。

假设一张图被分成了 \(S, T\) 两个部分，定义一个边集为割集当且仅当其中的 \((u, v)\) 满足 \(u \in S, v \in T\)（与普通割集不同，比如三元环）。也就是说只保留割集中的边，整张图就是一张二分图。

那么对于这 \(k\) 条边组成的集合，只需要其有一个子集为割集即可。

那如何快速判断一个边集 \(G\) 是否为割集呢？（神人做法）

我们先搞出一棵生成树（DFS 生成树较好），先考虑两条边的情况。（若一条非树边与一条树边在同一个简单环上，则称 “非树边覆盖树边”），建议画图。

• 如果有一条割边，显然可以。

• 如果两条边都是非树边，显然删除后啥事没有，不是割集。

• 如果都是树边，那么覆盖这两条树边的非树边集必须相同，这样才能使中间的部分和外界断开。

• 如果一条非树边，一条树边，那么覆盖树边的就只有这条非树边了。

但是如何判断覆盖两条树边的非树边集相等？答案是使用异或哈希。

对于每条边有个权值 \(a_e\)，对于每条非树边，随机一个权值 \(w\)，给它和它覆盖的树边的 \(a_e\) 都异或 \(w\) 即可（树上差分）。这时惊奇的发现对于两条边 \((u, v)\)，只需要 \(a_u = 0/a_v = 0/a_u \oplus a_v = 0\) 即可。实际前两个都可以不要，因为这个算一条边的割集，算子集时也会算到。

于是判断两条边组成的集合是否是割集，只需要 \(a_u \oplus a_v = 0\) 即可。

那么我们可以大胆猜测，多条边就是 \(val = XOR\{a_e\} = 0, e \in G\) 即可。

小小证明（伪证）一下，刚刚做的操作实际上是给每个环上的边都赋一个权值。而对于一个环来说，肯定有偶数条边在割集内（\(S - T - S - T - \dots - S\)），所以每个环对割集的贡献都是 \(0\)，所以一个割集，\(val\) 一定是 \(0\)。又因为你是随机化的，所以碰到若干个异或和不为 \(0\) 的数异或和为 \(0\) 的概率极低，所以可以认为它是正确的。

所以求出 \(a_e\) 后就是给定一个集合，问集合内是否有子集的异或和为 \(0\)，直接线性基即可。

时间复杂度：\(O(n + m + \sum k \log W)\)，\(W\) 是你随机的范围。

Gym 102984B

QOJ 也有。

给定一张 \(n\) 个点，\(m\) 条边的简单连通图。找到满足以下条件的边的子集的数量\(S⊆E\)：

• 删除 \(S\) 中的边使得图成为二分图。
• \(∣S∣≤2\)
• 不存在其他子集 \(T \sube E\)，使得\(∣T∣<∣S∣\) 并且满足前两个条件。

注意 \(S\) 可以为空。

\(n - 1 \le m \le 2.5 \times 10^5\)

这个题其实是很难的，但有了上个题的铺垫，就容易了一些。

我们知道如果保留割集中的边，是一张二分图。而且根据题目条件，要求 \(|S|\) 尽量小，那么二分图中的边一定可以组成割集。

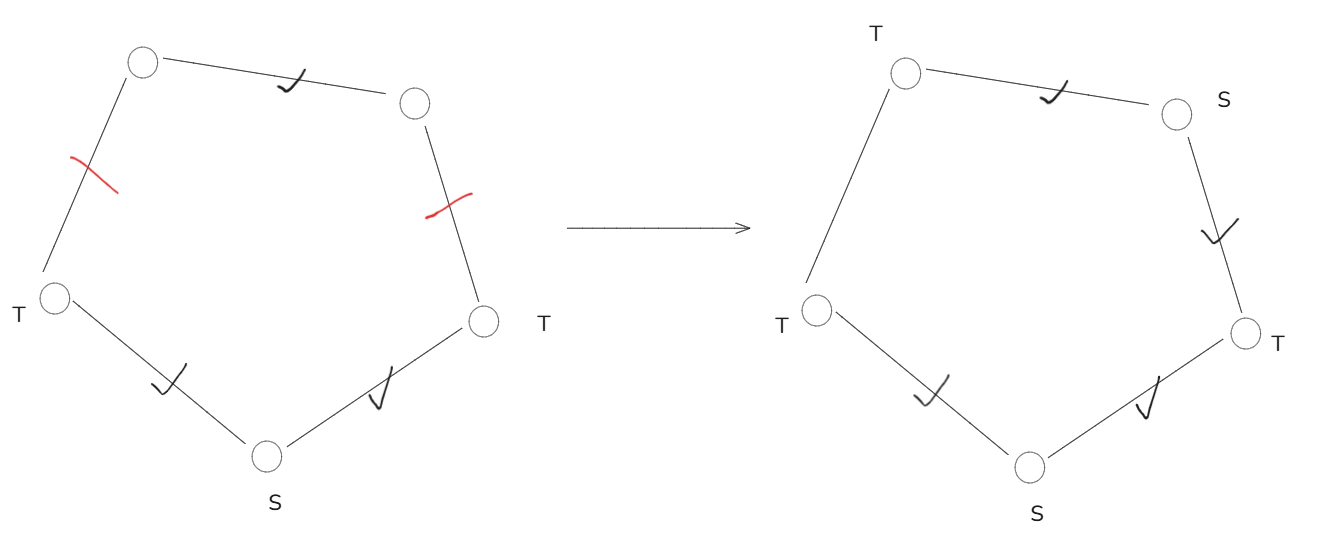
不会出现左图情况（只保留带钩的是一张二分图，但不是割集，割集还有加一条边），改为右图的选取方式即可。

具体的证明，如果一张二分图不是割集，随便取一组 \(S, T\) （二染色），把他们之间的边都加入割集即可。这样删除的边就变少了。

问题转化为，每条边有个权值，有删除尽量少的边，使得剩下的边的边权异或和为 \(0\)。

设 \(m\) 个数为 \(a_1 \sim a_m\)，\(s\) 为异或和。

• 若 \(s = 0\)，那么 \(S = \varnothing\)，答案为 \(1\)。
• 若存在 \(s = a_u\)，那么答案就是这种 \(a_u\) 的个数。
• 否则答案为 \(a_u \oplus a_v = s\) 的 \((u, v)\) 的对数。

随便做就行了。时间复杂度：\(O(m)\)。

话说好像这个题没有用到线性基，但不管了。