支配集

引入：CF765F

给定 \(n\) 个数的序列 \(a\) 以及 \(m\) 组询问，每组询问给定 \([l, r]\)，求 \(\min\limits_{l \le i < j \le r} \{ |a_i - a_j| \}\)。

\(n \le 10^5, m \le 3 \times 10^5, a_i \le 10^9\)。

一个很暴力的做法是莫队，用 set 维护做到 \(O(n \sqrt m \log n)\)，应该过不了。（似乎可以使用 64 叉线段树卡过。）

这个东西似乎没啥性质，从询问考虑似乎没啥前途。换个角度，看 \((i, j)\) 对于询问的贡献。

但是，\((i, j)\) 有 \(O(n^2)\) 对，是不能暴力枚举的，可以尝试挑出一些有可能产生贡献的数对进行枚举。但是也不需要做到只枚举产生贡献的，只要包含这些数对即可。形式化的说，设对答案有贡献的数对的集合为 \(S\)，我们只需要找到一个 \(T \supseteq S\)，满足 \(|T|\) 较小即可，称 \(T\) 为支配集。说白了就是丢掉一些没用的而已。

这个题，如果 \(x \le i < j \le y, |a_j - a_i| \le |a_x - a_y|\)，那么 \((x, y)\) 就可以从 \(T\) 中踢掉。

我们可以枚举 \(j\)，分 \(a_i \le a_j\) 以及 \(a_i > a_j\) 讨论，下面以 \(a_i \le a_j\) 的为例。首先最大的 \(i_0\) 满足 \(i_0 < j, a_{i_0} < a_j\) 肯定可以了。再找第二个 \(i_1 < i_0\)，要寻找一些限制条件：因为现在已经有了 \((i_0, j)\)，\((i_1, j)\) 要比 \((i_0, j)\) 更优需要满足 \(|a_j - a_{i_1}| < |a_j - a_{i_0}|\)（这是为啥要分两种情况讨论的原因），即 \(a_{i_1} > (a_{i_0} + a_j) / 2\)，找到最大的 \(i_1\) 即可。以此类推：\(a_{i_k} > (a_{i_{k - 1}} + a_j) / 2\)，不难得到 \(k \le \log V\) ，所以就找到一个支配集满足 \(|T| \le n \log V\)。

具体如何求 \(i_k\)，开一棵权值线段树记录每个区间中的数出现的最后一个位置，查询 \([(a_{i_{k - 1}} + a_j) / 2, a_{j}]\) 即可，做到找一个数对单次 \(O(\log n)\) 的复杂度。

求完支配集，就是一个二维数点的板子了。

时间复杂度：\(O(n \log n \log V + q \log n)\)。

一般有很多种支配集，只要包含所有可能的贡献情况且集合大小能接受就行。（比如全集也是一种支配集，只是过不了而已。）做不了的题可以想想支配集，去掉一些一定不可能产生贡献的情况。

QOJ-5148

给定一棵 \(n\) 个节点的树以及 \(q\) 组查询，每次给定 \(l, r\)，求 \(\min\limits_{l \le i < j \le r} \{ dis(i, j) \}\)。

\(n \le 2 \times 10^5, q \le 10^6\)。

这个题其实就是上个题的加强版，把序列拓展成树。

这样上个题的做法就失效了，因为有很多分支，要想另一种求支配集的方式。

做法也不多，因为求 \(\min\)，拆成 \(dep_{u} +dep_v - 2dep_{lca}\) 毫无用处，树链剖分之类的算法都不太行。考虑一下最暴力的点分治。‘

为了方便，三度化一下，搞边分治，只考虑两个子树的情况，计算经过中间那条边的 \((u, v)\)。

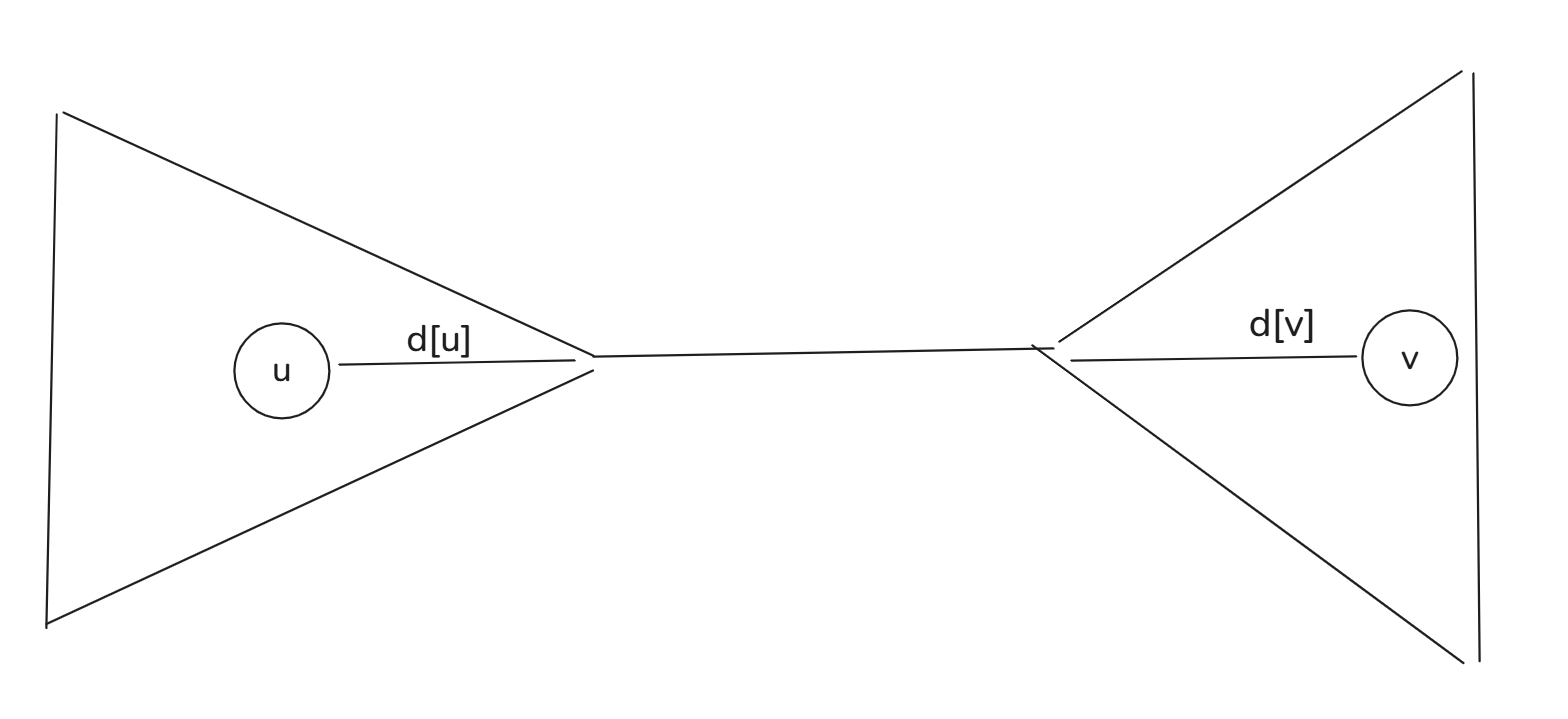
不妨设 \(d_u \le d_v\)，枚举 \(v\)，看有哪些 \(u\) 能有 \(v\) 配。那么 \(< v\) 的最大的 \(u\) 以及 \(> v\) 的最小的 \(u\) 肯定是可以的，然后其实就没了。

证明：设 \(u' < u < v\)，如果 \((u', v)\) 可以贡献，那么 \((u', u)\) 肯定也可以贡献。又因为 \(d_u, d_u' \le d_v\) 且 \((u, u')\) 在同一个子树，那么 \((u', u)\) 肯定更优。

所以对于一个分治中心，它对 \(|T|\) 的贡献是 \(O(sz)\) 的，所以可得到一个 \(|T| \le n \log n\) 的 \(T\)。

求 \(u\) 用个树状数组即可，查询仍是二维数点。

时间复杂度：\(O(n \log^2 n + q \log n)\)。

总结

支配集只是一种思想，具体如何找需要具体分析，且可以有很多种求法（引入题应该也可以分治）。

通过找到一个包含所有可能贡献情况且 \(sz\) 尽可能小的 \(|T|\) 来优化时间复杂度。一般在没啥性质时可以考虑。

常见的找法就是先找到一些比较显然的，通过已知的在支配集的元素来限制新加进来的，使用反证法。（如果 \(a\) 在支配集内且 \(a + b < a + c\) 肯定就不用选 \(c\) 了。）