动态直径问题

动态直径问题，就是在修改点权/边权（或者其他）的基础上维护直径。一般可以使用 欧拉序+线段树（*），点分树 )（也许可以线段树分治/动态 DP）求解。需要根据实际情况进行选择。

洛谷 P2056

给定一棵 \(n\) 个节点树，每个节点有黑/白两种颜色，动态维护黑点之间的距离最大值。

线段树分治

这个做法似乎没啥优点，但讲讲吧。（备用方案。）

这个做法需满足权值非负。

可以把每个点看成出现在某一段时间内，加入这一段区间。

在无负权的前提下有一个性质，加入一个点 \(u\)，直径只有 \(2\) 种情况：原直径/原直径的一个端点 + \(u\)（证明用距离一个点最远的点一定是直径端点的性质），所以只需要维护直径端点，加入时把几种情况都算出来即可。

求距离可能需要带个 \(\log\)，总共 \(O(q \log ^ 2 n)\)。或者使用欧拉序转为 RMQ，但这样直接线段树即可。

点分树

两个黑点之间是一条路径，对于路径问题可以考虑点分治做（动态的就是点分树）。

对于一个分治中心 \(x\)，设他有 \(k\) 个儿子 \(son_1 \sim son_k\)，对于每个儿子维护其子树内 \(d_{max}\)，然后经过 \(x\) 的答案就是最大的两个 \(d_{max}\) 之和。

因为涉及删除，对于每个儿子需要开个 set 维护 \(d_{max}\)，\(x\) 也要开个 set 维护儿子 \(d_{max}\) 的顺序，全局还需要开个 set，实在有一点点点点麻烦。可以尝试用边分树代替，这样就只有两个儿子，\(x\) 就不需要 set 了。（边分治的优点就是只有两个儿子，缺点是需要三度化，要处理好虚点，这个题只需改改边权即可。只三度化但还是点分治应该也是可以的）

卡常技巧（仅限于只需要最大值）：因为 set 常数巨大，尝试用 pq 代替。开两个 pq1, pq2，pq1 维护加入的，pq2 维护删除的。求最大值时 if (pq1.top() == pq2.top()) 就都 pop 掉，一直执行到 pq1.empty() || pq2.top() != pq2.top()。实测优化至少两倍常数。

时间复杂度：\(O(q\log^2n)\)。

比较万能（暴力），不需要满足权值非负，但常数较大，有时写起来很恶心（下题）

CF1192B

有一棵 \(n\) 个点的带边权树，\(q\) 次操作，每次修改某条边的边权，输出树的直径大小。强制在线。

如果暴力点分树的话，对于每棵子树都需要开一棵线段树维护区间加法（一条边加等价于某个子树距离根的距离加），太恶心了。同时又强制在线，无法线段树分治。需要用到第三种方法。

先讲讲欧拉序（我以前似乎没怎么学过），它和 dfs 序，括号序都不一样。按照 dfs 序的过程（包括回溯），把经过的点依次加进来。

如下图，这棵树的一个欧拉序是：1 2 3 4 3 5 6 5 3 2 7 8 7 2 9 2 1 10 11 10 1。

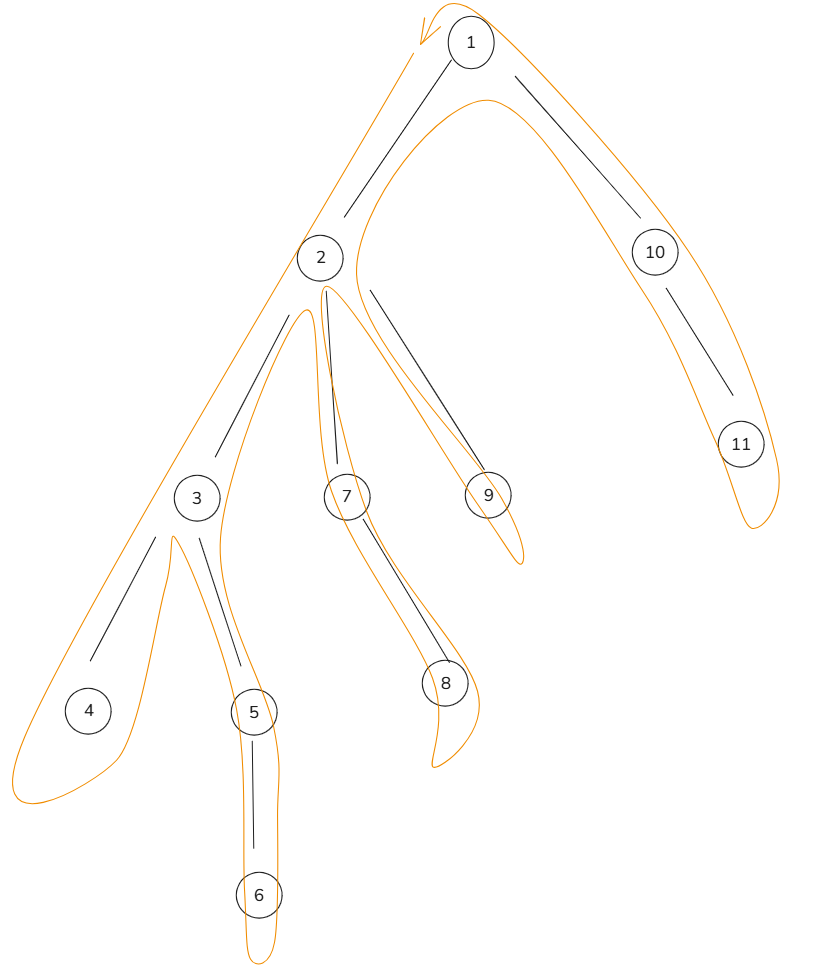
欧拉序有什么性质呢？对于 \(u, v\) 来说，找到欧拉序中任意的一个 \(u\) 和一个 \(v\)，设为 \(x, y\)，\(\text{LCA}(u, v)\) 就是 \(x \sim y\) 之间深度最小的。因为 \(u \rightarrow v\) 之间一定会经过 \(\text{LCA}\) 且不会继续向上。（例如 \(u = 5, v = 8\)，找到了一段：5 6 5 3 2 7 8 ）

基于这个性质，就可以将 \(\text{LCA}\) 问题转化成 RMQ 问题了。

---

对于这个题，直径就是要求 \(\max \{dis(u, v)\}\)，转化成 \(dep_u + dep_v - 2dep_{lca}\)。丢到欧拉序上就是要找到 \(i \le j \le k\) 使得 \(d_i + d_k - 2d_j\) 最大（\(d\) 为欧拉序对应节点的 \(dep\)）。

用线段树维护区间 \(d_{\max}, d_{\min}, (d_{i} - 2d_j)_{\max}, (d_k - 2d_j)_{\max}, ans\)，转移分全在左/右以及一些左一些右转移即可。修改就是一个子树加，不难发现欧拉序和 dfs 序一样每个子树都对应一段区间，转为区间加即可。

前面那个题也是可以类似的做的。

时间复杂度：\(O(q \log n)\)。

不难发现，当边权为负时，\(dep\) 最小的可能就不是 \(\text{LCA}\) ，所以这种方只适用于边权非负的情况。