NOI2023

D2T1

对于 \(dis(x, y)\) 来说，肯定是从 \(x\) 先走到 \(\text{LCA}(x, y)\) 再走到 \(y\) 的。所以只需要求出祖先到后代的 \(dis\) 即可（这也是为啥要是二叉树，保证 \(h\) 只有 \(n\)），然后可以轻松计算两个子树之间的距离之和。

接下来有两种角度：在祖先计算它到所有儿子的 \(dis\)/在儿子计算所有祖先到它的 \(dis\)。（显然后者看起来就简单些，因为前者要子树大小不确定，而后者祖先个数是有 \(n\) 个。）

不幸的是我选择了前者。

---

我的做法是这样的：从 \(x\) 出发要到达它的子树内，一定是先 \(x \rightarrow u \rightarrow v (u 为 x 的祖先)\)，再从 \(v\) 出发走 \(v \rightarrow \text{LCA(v, y)} \rightarrow y\)。

第一步可以枚举 \(v\) 以及它连接的 \(u\) 进行更新。然后对 \(x\) 的子树从下往上跑一遍，算出 \(dis(x, \text{LCA}(u, v))\)，最后再利用 \(\text{LCA}(u, v)\) 到子树内的信息进行更新即可。

这种方式将 \(x\) 到 \(y\) 的路径拆成若干段，分开进行计算，但是有些复杂。因为 \(sz(x)\) 最大有 \(n\)，还要拍到 dfs 序上搞，有点恶心。

写的时候忘记 \(v\) 可以先走到 \(\text{LCA(v, y)}\) 再走下去到达 \(y\)，直接用 \(v\) 的子树信息更新 \(dis(v, y)\)，导致调了 \(2h\)。

时间复杂度

第一步，对于 \(v\) 来说，每个 \(v\) 的祖先 \(x, u\) 都要枚举一次到达 \(v\) 的边，总共是 \(O(n^2m)\)。

第二步，求 \(dis(x, \text{LCA}(v, y))\) 是 \(O(sz(x))\) 的，利用 \(dis(\text{LCA}(v, y), y)\) 更新是总共也是 \(O(sz(x))\) 的。

总时间复杂度：\(O(n^22^n)\)。

---

题解选择了后者，记 \(f_{x, i}\) 表示 \(x\) 的 \(i\) 级祖先 \(y\) 的 \(dis(y, x)\)。

因为 \(y\) 到 \(x\) 的路径一定是形似下图的，可以拆解成 “一上一下，一上一下，一上一下，……” 的形式，所以只需要处理一个 “一上一下” ，然后往上跳就行。

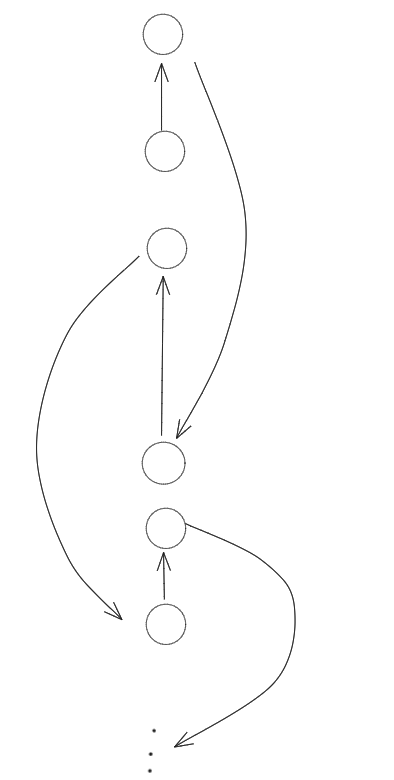
倒过来，从 \(y\) 开始就是 “一下一上” 的形式， 为了方便可以枚举一条边 \((u, v)\)，然后枚举 \(v\) 的祖先 \(y\) 更新 \(dis(u, y)\) 对应的 \(f_{y, i}\) 。

处理好了一个段就好做了，\(f_{u, i}\) 可以从 \(f_{f_{u, j}, i - j}\) 更新过来（有点倍增的意思），就做完了。

别忘了，走后可能还有一个“下”，这个用 \(f_{u, j}\) 更新一下 \(f_{u, i}(j > i)\) 即可。（或者把每一段改成“一上一下一上” 也可以。）

时间复杂度同样是 \(O(n^22^n)\) 。

---

两种方式本质上差不多，但是第二种就是好写很多，因为第一种子树大小不固定（其实是一个 "一上一下一上" 的过程）。。。

选择合适的角度看待问题会有很大差别。

D2T2

比较 \(s[i:i + l - 1]\) 与 \(R(s[i + l : i + 2l - 1])\) 是比较难的，可以先比较 \(s[i : n]\) 与 \(R(s[1, i + l])\)，搞个后缀数组即可（把 \(s\) 与 \(R(s)\) 用 # 分隔 ）。

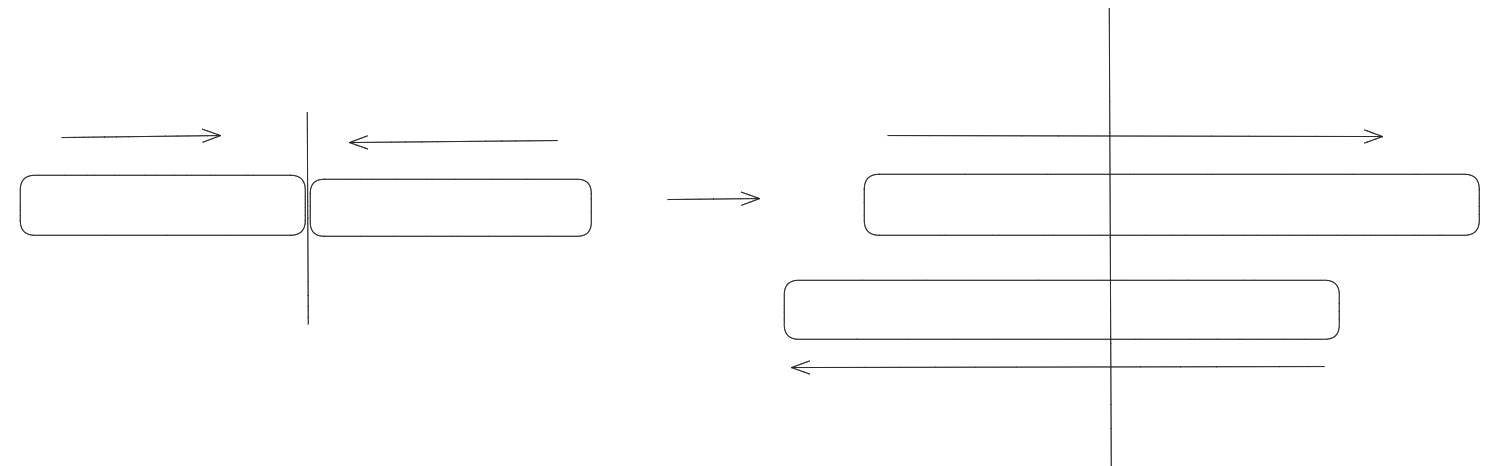
设 \(s[i : n]\) 的排名为 \(rnk_i\)，\(R(s[1, i])\) 的排名为 \(rnk_{i + n}\)。

因为 \(s[i : i + l - 1] < R(s[i + l : i + 2l - 1])\)，那么 \(rnk_{n + i + 2l - 1} > rnk_i\)，又有 \(l \le r\)，转化一下个二位数点。（有多少个 \(i < x < 2r\) 满足 \(rnk_x > rnk_i\)，似乎要分奇偶性算。）

---

但那个只是一个充分条件，还要减去 \(s[i: i + l - 1] = R(s[i + l : i + 2l - 1]) \ \&\& \ s[i : i + l - 1] < R(s[i + l : i + 2l - 1])\) 的情况 。

前面那个条件就是回文串的条件，所以可以想到回文串经典套路枚举中点 \(x\)，可以用 Manacher/二分 + 哈希 求出回文半径 \(f_x\)，就是要减去有多少个 \(x\) 满足 \(i \le x < r \ \& \& \ x - f_x + 1\ge i\) 。

第二个条件相当于要求 \(s_{x + f_x} < s_{x - f_x}\)，此时 \(rnk_i < rnk_{n + i + 2l - 1}\)。然后要变成了二维数点。

所以时间复杂度是 \(O((n + q) \log n + SA)\)。

因为子串可以看成后缀的前缀，可以先求出后缀的答案，再减掉不满足条件的。发现变成关于回文串的问题，运用经典套路求出回文半径做即可。