NOIP2024

T3

Task 1 ~ 6： k = 1

这个部分就是只有一条关键边。

根据题目的性质，一个点 \(u\) 连的所有边肯定会形成一条链（推推样例吧）。而第一条访问到 \(u\) 的边一定是链头，剩下还有 \(deg_u - 1\) 条，共有 \((deg_u - 1)!\) 种排列方式。所以答案为 \(\prod\limits_{u = 1}^n (deg_u - 1)\)。

时间复杂度：\(O(n)\)。

再高点链和菊花图的特殊性质可以拿到 \(40pts\)。

Task 7 ~ 10：k = 2

这时答案肯定不是 \(k = 1\) 时的答案 \(\times 2\) 了，需要减去重复的。

如果 \(u\) 在 \(e_1\) 至 \(e_2\) 的路径上（只有两个端点不算），那么 \(u\) 对应的那条链的链头和链尾都确定了（一头是最靠近 \(e_1\) 的那条，一头是最靠近 \(e_2\) 的那条 ），所以方案数是 \((deg_u - 2)!\)。

如果 \(u\) 不在 \(e_1\) 至 \(e_2\) 的路径上，实际上只有一个链头是确定的（最靠近 \(e_1 \rightarrow e_2\) 这条链的边），所以方案数是 \((deg_u - 1)!\)。

所以总方案数是 \(2\prod\limits_{u = 1}^n (deg_u - 1) - \prod\limits_{u = 1}^n (deg_u - 1 - [u 在 e_1 \rightarrow e_2 上])\)。化简一下，\(\prod\limits_{i = 1}^n (deg_u - 1)(2 - \prod\limits_{v 在 e1 \rightarrow e_2 上} \frac{1}{deg_v - 1})\)。

正解

都有 \(k = 2\) 的做法了，接下来自然就考虑容斥了。

假设现在选择了 \(m\) 条关键边 \(e_1 \sim e_m\)，求有多少棵新树可以同时由这 \(m\) 条边出发生成。

根据 \(k = 2\) 时的经验，其实能发现一个结论：这 \(m\) 条边一定在一条链上。不然就会出现下图的情况（蓝色的为关键边）。然后发现 \(u\) 连的边没法排，因为橙色边一定要占据一个链头，但总共在两个。所以显然方案数为 \(0\)。

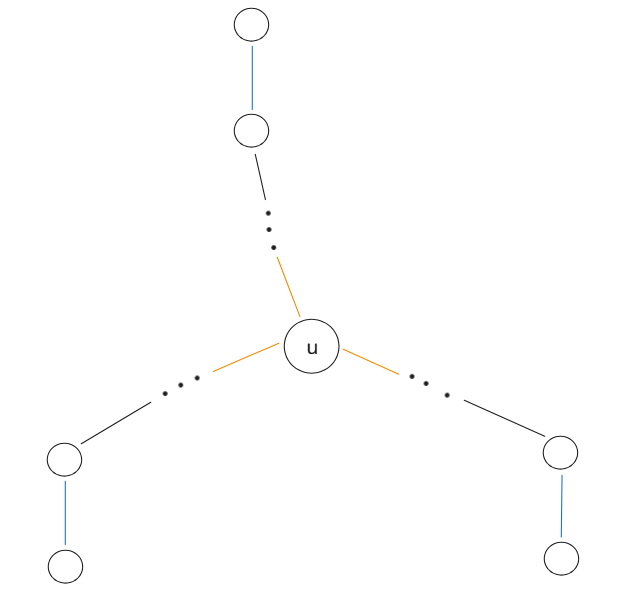
进一步的，假设这 \(m\) 条关键边在链上是按照 \(e_1, e_2, \dots e_m\)，实际上方案数和只有 \(e_1, e_m\) 是一样的（是个人就看的出来吧）。

所以我们考虑对于关键边对 \((e_i, e_j)\) 来说它们的贡献是什么？

• 如果 \(e_i\) 到 \(e_j\) 的路径上没有别的关键边了，贡献显然是 \(-1\)。
• 否则不妨设有一条 \(e_k\)，那么选择 \(e_k\) 的不选 \(e_k\) 的方案数一样多，但是系数一个是 \(1\)，一个是 \(-1\)，抵消了。贡献为 \(0\)。

所以我们只用考虑 ”相邻的“ 的边对的贡献即可。需要求出 \(s = \sum\limits_{(e_i, e_j)}\prod\limits_{v 在 e_i \rightarrow e_j 上} \frac{1}{deg_v - 1}\)，答案为 \(\prod\limits_{u = 1}^n (deg_u - 1)(k - s)\)。

至于 \(s\) 怎么求，对于 \((e_i, e_j)\) 在 \(\text{LCA}\) 算贡献，玩个树形 DP 即可。

时间复杂度：\(O(Tn)\)。

评价

这个题部分分给定还是很有引导性的，从 \(k = 1\) 到 \(k = 2\) 再推广到一般情况。

关键是从 \(k = 1\) 得到从点的角度考虑问题，再从 \(k = 2\) 想到容斥，接着推出 \(e_1 \sim e_m\) 要在一条链上才有方案数，然后算出 \((e_i, e_j)\) 的贡献算出答案的式子，最后就可以跑个树形 DP 。

T4

首先我们考虑一个节点 \(u\) 对答案的贡献。假设 \(u\) 子树内的数形成了若干个极大的连续段 \([l, r]\)，若 \([ql, qr]\) 与某个 \([l, r]\) 的交集至少为 \(k\) 就有 \(dep_u\) 的贡献。

所以我们来考虑如何维护这个极大的连续段。一个比较显然的方式是并查集，加入一个元素 \(x\) 后，只可能将 \(x - 1, x, x + 1\) 所在的集合连到一起，只需要用 \(x\) 现在所在的集合进行贡献。

但是我们也不可能将每次将 \(u\) 内所有元素都扫一遍，那就爆了。这时我们就可以想到启发式合并，每次 \(u\) 从 \(son_u(u 的重儿子)\) 继承过来，这样总共至多加入 \(O(n \log n)\) 的元素了。而且这样做显然是正确，因为只会漏算只包含 \(son_u\) 子树的连续段，而这个显然 \(son_u\) 贡献更优。

所以我们就拥有了 \(m(m \le n \log n)\) 个可能贡献的区间，接下来就比较好办了。对于 \(l < ql\) 的，只需要满足 \(r \ge ql + k - 1\)；对于 \(l \ge ql\) 的，只需要满足 \(r - l + 1 \ge k, l \le qr - k + 1\)，化简一下 \(ql \le l \le qr - k + 1 \&\& r - l + 1 \ge k\)。就是两个二维数点，搞个线段树即可在 \(O((m + q) \log m)\) 的时间内解决。

所以我们就拥有了时间复杂度最坏为 \(O(n \log^2n)\) 的做法，其实已经能过了。但是还有更优秀的做法。

---

对于后半部分其实没办法优化了，只能优化前半部分。我们仔细分析，只有当两个集合合并时才有会产生一个贡献区间，而总共只有 \(n\) 个数，也就是最多只有 \(O(n)\) 个有用的区间。

但是启发式合并已经没有前途了。不过也许你知道这个结论：\(dep_\text{LCA*(l, r)} = \min\limits_{i = l}^r dep_{\text{LCA(i, i + 1)}}\)。那我们可以求出所有 \(\text{Lca(i, i + 1)}\)，用单调栈（笛卡尔树）求出这个它为最小值的区间，这就可以得到 \(O(n)\) 个区间了，不难发现它是包含了所有情况的。

时间复杂度来到了 \(O(n \log n)\)。

评价

一条链的部分分有利于可以让我们想到使用若干个有用的贡献区间 \([l, r]\)来贡献答案。（似乎容易去想线段树上二分，而非并查集，并且容易误导人，以为新增的区间一定包含 \(u\)，反正我被坑了。）

两只 \(\log\) 的做法还是比较粗暴的，单 \(\log\) 需要知道一个结论。（我想到另一个结论：找 \(dfs\) 最小和最大的算 LCA，然后没有任何前途）

似乎搞完 SA 后也一般是笛卡尔树或者并查集进行合并。