NOIP2023

参考了这篇 题解。图片是题解里的。

T3

NOIP2023 双序列拓展

首先，对于任意的 \(1 \le i, j \le l_0, (f_i - g_i)(f_j - g_j) > 0\)，其实就是要么所有 \(f_i < g_i\)，要么 \(f_i > g_i\)，可以根据 \(x_1, y_1\) 判断出来。后面都不妨设 \(x_i < y_i\)。

感觉 \(T\) 组只是为了减少输入量。

Task 1 ~ 7

一个比较暴力的 DP，令 \(dp_{i, j}\) 表示是否可以有某个 \(k\) 满足 \(f_k= x_i, g_k = y_i\)。显然 \(dp_{i, j}\) 可以转移到 \(dp_{i + 1, j}, dp_{i, j + 1}, dp_{i + 1, j+1}\)。表示后面的 \(f, g\) 的选法。

时间复杂度：\(O(Tnm)\)。

Task 8 ~ 14 特殊性质分

我们先将上面那个做法 “可视化”，用图形刻画出来。

其实就是有一个 \(n \times m\) 的网格，每个格子是 \(0/1\)，从 \((1, 1)\) 出发，每次只能向下、向右、向右下走且只能经过为 \(1\) 的格子，问能否到达 \((n, m)\)。

考虑一些必要条件。首先必须有 \(\min \{x_i\} < \min\{y_j\}\)，不然有一列就全是 \(0\) 了。同理，\(\max \{x_i\} < \max \{ y_j\}\)，否则有一行就全是 \(0\) 了。

满足了这两个条件，那么第 \(minx\) 行和第 \(maxy\) 列（最小值/最小值的位置）就全是 \(1\) 了，考虑特殊性质就是第 \(n\) 行和第 \(m\) 列全是 \(1\) 了。也就是说只要我们能走到第 \(n - 1\) 行或者 \(m - 1\) 列就万事大吉了。（如下图）

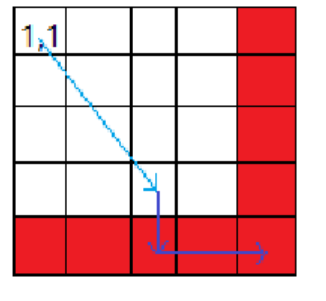
这时我们再对前 \((n - 1) \times (m - 1)\) 个格子重新考虑必要条件。如果有 \(\min \{x_i\} < \min\{y_j\}\)（第 \(minx'\) 行全为 \(1\) 了），那么问题变为了第 \(minx'\) 行第 \(m\) 列为 \(1\) 了，那么就可以递归下去了。

对列也是一样的。如果有 \(\max \{x_i\} < \max\{y_j\}\)（第 \(miny'\) 列全为 \(1\) 了），那么问题变为了第 \(n\) 行第 \(miny'\) 列为 \(1\) 了，也是可以递归下去的。

如果上面两个条件均不满足，那就说明有一行一列全是 \(0\) 了（去掉最后一行和最后一列），无解了。

于是你就可以一直所有网格图的范围，直到只有 \(1\) 行或 \(1\) 列就代表有解了。

因为每做一次，网格至少缩小一行一列。所以时间复杂度是 \(O(T(n + m))\) 的。

bool check(int n, int m) { // 只用前 n 行 m 列
	if (n == 1 || m == 1) return 1; // 有解
	auto u = prea[n - 1], v = preb[m - 1];
	if (a[u.mx] < b[v.mx]) return check1(n, v.mx); // 某一列全是 1
	if (a[u.mi] < b[v.mi]) return check1(u.mi, m); // 某一行全是 1
	return 0; 
}

正解

会了特殊性质，基本就做完了，特殊性质具有极高的提示性。

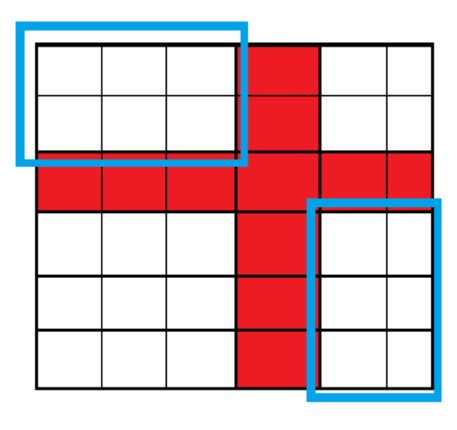
特殊性质是 \(x\) 的最大值和 \(y\) 的最小值均在最后一个，即网格中的最后一行和最后一列均是 \(1\)。没有了这个条件，就相当于这一行和一列的位置发生了变化（如下图）。那么只需要 \((1, 1)\) 能走到红色部分，红色部分又能 \((n, m)\) 就可以了。 对着左上部分和右下部分都做一遍即可。

时间复杂度仍为 \(O(T(n + m))\)。

NOIP 题的特殊性质都是很有提示性的（神秘的），思考如何往上面靠会变得简单一些。

这个题其实想到了将暴力 DP 变成网格图的形式就成功了一半了。