FFT
给定两个 \(n\) 次多项式 \(A, B\),要求出 \(C = A \times B\)。本文将讲述一个能在 \(O(n \log n)\) 的时间内快速计算的方法:FFT,比 \(O(n^2)\) 的朴素算法更加高效。并且因为两个整数的乘法可以被认为是多项式乘法,这个算法也可以优化高精度运算。
流程
首先我们将一个 \(n - 1\) 次多项式转为 \(n\) 个点值:\(f = \sum\limits_{i = 0}^{n - 1} a_i x^i \iff f(x_0), f(x_1), \dots f(x_{n- 1})\)。两种形式是可以互相转换的。
这有什么好处呢?\(C(x_i) = A(x_i)B(x_i)\),这样乘法的时间复杂度就是 \(O(n)\) 的了。现在只需要将求出 \(A, B\) 的点值表示 (DFT),$O(n) $算出 \(C\) 的点值表示,再转为多项式形式 (IDFT)即可。这个求点值的方式就是 FFT 啦。
FFT方法 (O(n log n)):
系数 A -- DFT --> 点值 A --\
|--逐点相乘 (O(N)) --> 点值 C -- IDFT --> 结果系数
系数 B -- DFT --> 点值 B --/
现在我们来求点值,以 \(n = 7\) 为例:
令 \(g(x) = f_0x^0 + f_2x^1 + f_4x^2 + f_6x^3, h(x) = f_1x^0 + f_3x^1 + f_5x^2 + f_7x^3\)。
那么原来的 \(f(x) = g(x^2) + xh(x^2)\),而且 \(f(-x) = g(x^2) - xh(x^2)\)。
所以我们要计算 \(x = 1, -1\) 的 \(f(x)\) 就变快了(复杂度 / 2),只需要计算 \(g(1)\) 和 \(h(1)\) 即可。进一步来说,对于所有 \(x, x'\) 满足 \(x^2 = (x')^2\),都可以只计算 \(g(x^2), h(x^2)\) 就快速得到答案。这也是 FFT 比暴力更快的原因。
现在来到子问题,令 \(y = x^2\),计算 \(g(y)\)。还是要找到 \(y, y'\) 满足 \(y^2 = (y')^2\),比如 \(y = 1, y' = -1\),此时对应的 \(x = 1, -1, i, -i\)。
基于这个想法(每次使得 \(x^2 = (x')^2\)),我们就得到了 \(x\) 的取值。要两个 \(x\) 时为 \(1, -1\),\(4\) 个 \(x\) 为 \(1, -1, i, -i\),八个 \(x\) 为 \(\dots\)。不断开根即可。
相信大家已经学了点复数,最后得到的点值就是 \(\omega_n, \omega_{n}^2 \dots \omega_{n}^{n - 1}\)(\(\omega_n\) 为 \(n\) 次单位根)。
此时我们将 \(n\) 补成 \(2^m\) 方便计算:
(将 \(f_0, \dots f_{n - 1}\) 变为 \(F_0 \dots F_{n - 1}\) 就是离散傅里叶变换(DFT))。
现在要求 \(f_0 \sim f_{n - 1}\) 离散傅里叶变换的结果 \(F\),只需要分别求出 \(f_0, f_2, \dots f_{n - 2}\) 与 \(f_1, f_3 \dots f_{n - 1}\) 离散傅里叶变换的结果 \(G, H\)。
由单位根的性质 \((\omega_n^k) ^ 2 = \omega_{n / 2}^{k}\) (下面 \(1 \le i \le n / 2\)):
又因为 \(\omega_{n}^{k + n / 2} = -\omega_{n}^k, (\omega_{n}^{k + n / 2}) ^ 2 = (\omega_{n}^k) ^ 2\):
\(F_{i + n / 2} = G_i + \omega_{n}^{i + n / 2} H_i = G_i - \omega_{n}^i H_i\)。
所以我们可以在 \(T(n) = n + 2T(n / 2) = n \log n\) 的时间求出 \(F\)。
现在我们终于求出 \(A, B\) 的点值表示,也就得到 \(C\) 的点值表示,但还要将点值转为多项式形式。将点值转为多形式只需要求 \(\omega\) 时三角函数改改符号 (\(\omega_n \rightarrow \frac{1}{\omega_n}\)),最后除个 \(n\) 即可 (具体见代码)。(不要问我为什么,因为我也不知道。或许你可以尝试理解一下: OI Wiki)
struct Comp { // 复数
double x, y;
...
};
void DFT(Comp *f, int n, int rev) { // rev = 1, DFT; rev = -1, IDFT
if (n == 1) return ;
for (int i = 0; i < n; i++) {
t[i] = f[i];
}
for (int i = 0; i < n; i++) { // 偶数放到左边,奇数放到右面
if (i & 1) f[i / 2 + n / 2] = t[i];
else f[i / 2] = t[i];
}
Comp *g = f, *h = f + n / 2;
DFT(g, n / 2, rev), DFT(h, n / 2, rev); // 递归
for (int i = 0; i < n / 2; i++) {
Comp ormega = {cos(2 * PI / n * i), sin(2 * PI * rev / n * i)}; // wn^i,累乘快一些,但精度可能有问题。
t[i] = g[i] + ormega * h[i];
t[i + n / 2] = g[i] - ormega * h[i];
}
for (int i = 0; i < n; i++) {
f[i] = t[i];
}
}
非递归写法
虽然上面的递归是 \(O(n \log n)\),但递归的常数巨大,因此我们一般不会选择递归。
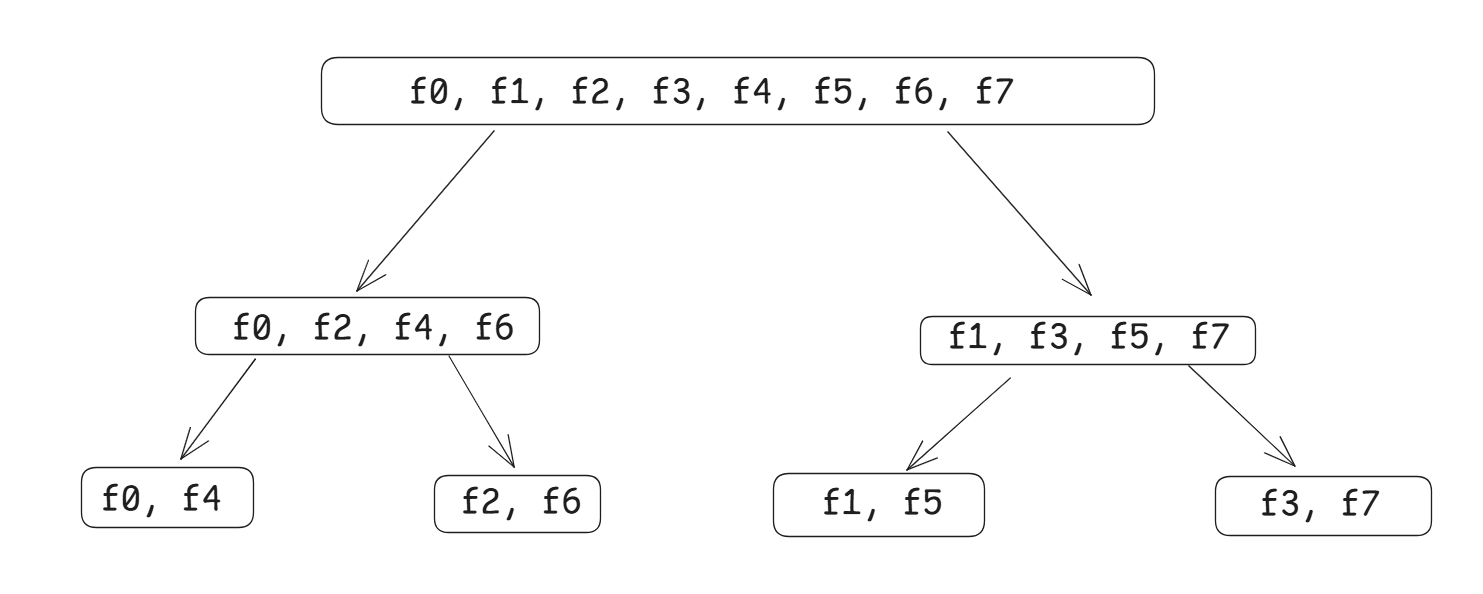
非递归版本的第一步就是重新排序系数(内存访问连续),\(f_0 \sim f_7 \rightarrow f_0,f_4,f_2,f_6,f_1,f_5,f_3,f_7\)。
怎么换呢?观察一下:\(0 = 000, 4 = 100, 2 = 010, 6 = 110, 1 = 001, 5 = 101, 3 = 011, 7 = 111\)。把二进制翻转以后就是 \(0 \sim 7\)。这一步的名字叫位逆序置换(其实不重要)。
排好序后,我们将递归的过程改为从下往上计算,\(f_i\) 与 \(f_{i + 2^k}\) 的计算的结果放回 \(f_i, f-{i+ 2^k}\) 即可。
void change(int n, Comp *a) { // 位逆序置换
// i 二进制倒过来是 rev[i]
for (int i = 1; i < n; i++) {
rev[i] = (rev[i >> 1] >> 1) + (n >> 1) * (i & 1); // 如果最后一位是 1,反转成 n / 2
}
for (int i = 0; i < n; i++) {
if (rev[i] < i) swap(a[i], a[rev[i]]);
}
}
void FFT(int n, Comp *a, int rev) {
change(n, a);
for (int i = 0; i < n; i++) { // 预处理 n 次单位根
w[i] = {cos(rev * 2 * PI * i / n), sin(rev * 2 * PI * i / n)}; // cos 的 rev 不乘也没事(诱导公式)
}
// 长度为 1 的合并为长度为 2 的,长度为 2 的合并为长度为 4 的,...
for (int o = 2; o <= n; o <<= 1) {
for (int i = 0; i < n; i += o) {
for (int x = 0; x < o / 2; x++) {
// w[n / o * x] 为 o 次单位根的 x 次方
auto u = a[i + x], v = a[i + x + o / 2] * w[n / o * x];
a[i + x] = u + v;
a[i + x + o / 2] = u - v;
}
}
}
if (rev == -1) {
for (int i = 0; i < n; i++) {
a[i].x /= n, a[i].y /= n;
}
}
if (rev == -1) { // IDFT
for (int i = 0; i < n; i++) {
a[i].x /= n, a[i].y /= n;
}
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号