学习率衰减优化和正则化

学习率衰减优化

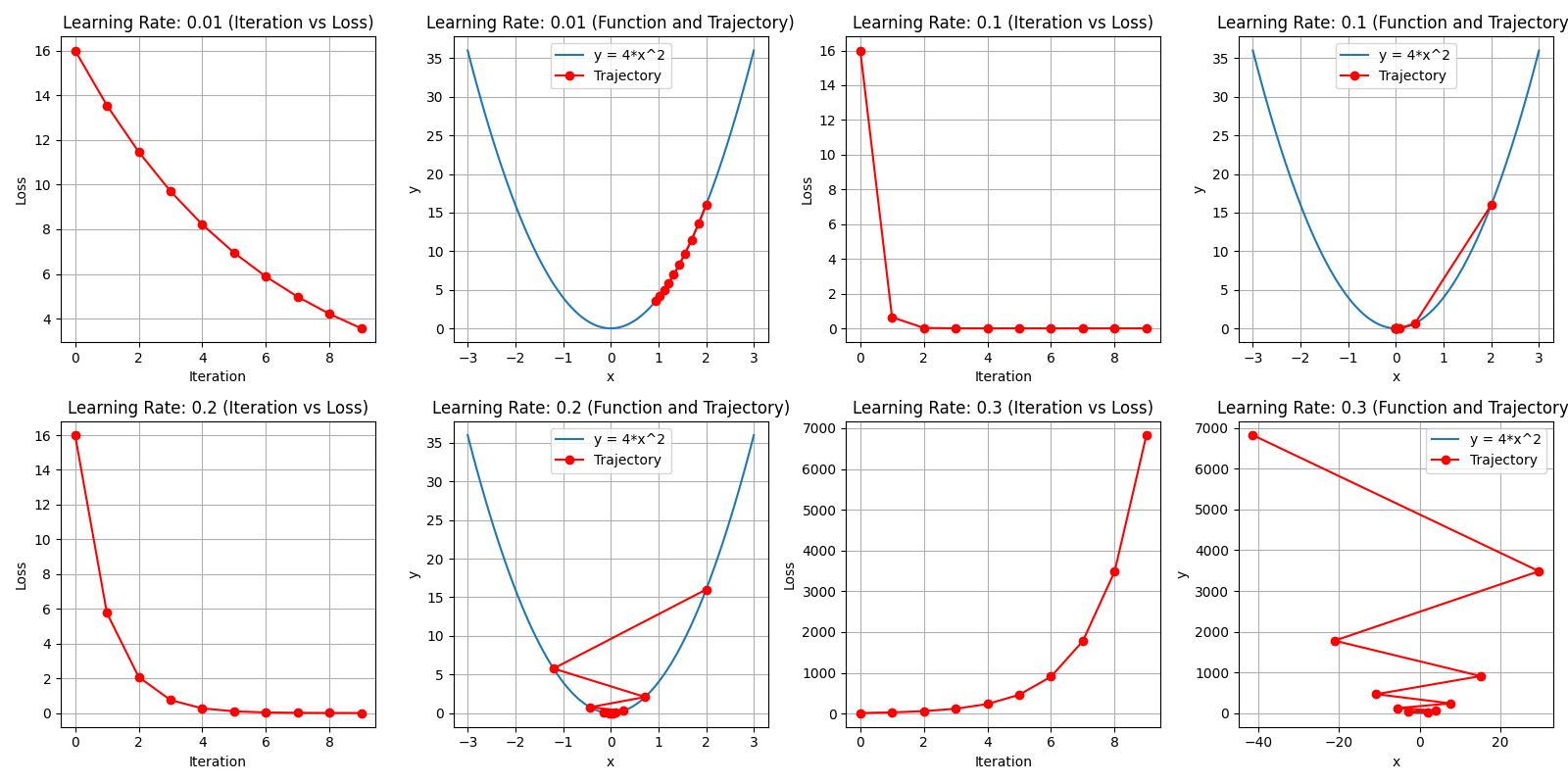
在训练神经网络时，学习率通常需要随着训练过程动态调整。主要原因如下：

训练后期若学习率过高，可能导致损失函数在最小值附近震荡，难以收敛
若学习率减小过慢，则收敛速度会变慢，训练时间延长
若学习率减小过快，则可能陷入局部最优或提前停止学习

学习率衰减策略通过动态调整学习率，平衡收敛速度与精度，帮助模型更好地收敛到最优解。

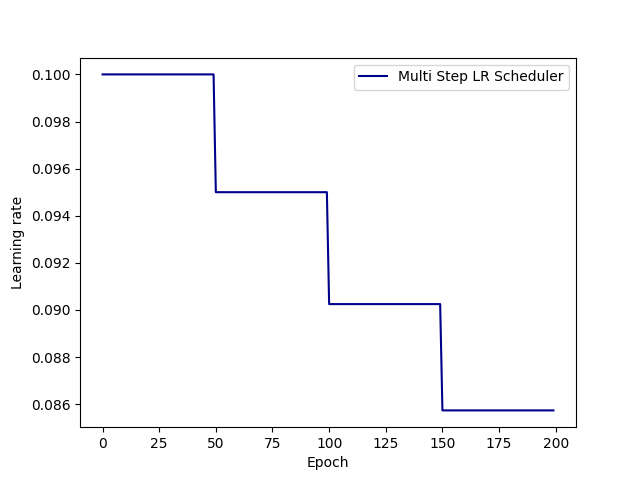
1. 等间隔学习率衰减（StepLR）

每隔固定的训练周期（epoch）将学习率乘以一个衰减因子。

数学公式：

\[\eta_t = \eta_0 \times \gamma^{\lfloor t/s \rfloor} \]

其中：

\(\eta_t\) 是第 \(t\) 个 epoch 的学习率
\(\eta_0\) 是初始学习率
\(\gamma\) 是衰减因子（通常为 0.1-0.9）
\(s\) 是衰减间隔（每隔多少 epoch 衰减一次）
\(\lfloor \cdot \rfloor\) 表示向下取整

PyTorch实现：

# 等间隔学习率衰减
# 调整方式：lr = lr * gamma，每隔step_size个epoch衰减一次
scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.1)

特点：

简单直观，易于实现
在固定间隔后突然降低学习率
适用于训练过程有明显阶段性的场景

myplot2

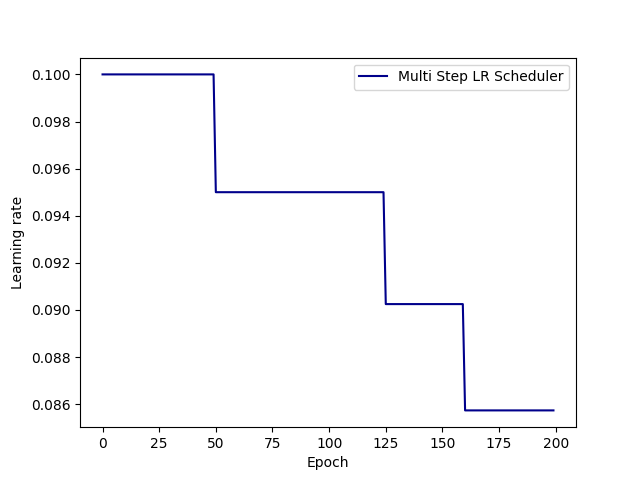
2. 指定间隔学习率衰减（MultiStepLR）

在指定的训练周期（epoch）将学习率乘以衰减因子。

数学公式：

\[\eta_t = \eta_0 \times \gamma^{\sum_{i=1}^k I(t \geq m_i)} \]

其中：

\(m_i\) 是第 \(i\) 个衰减里程碑（milestone）
\(I(\cdot)\) 是指示函数，当条件为真时值为 1，否则为 0
\(k\) 是里程碑总数

PyTorch实现：

# 指定间隔学习率衰减
# 调整方式：lr = lr * gamma，在milestones指定的epoch进行衰减
scheduler_lr = optim.lr_scheduler.MultiStepLR(
    optimizer, 
    milestones=[50, 125, 160], 
    gamma=0.1
)

特点：

更加灵活，可以在训练的不同阶段调整学习率
适用于训练曲线有多个明显转折点的场景

myplot3

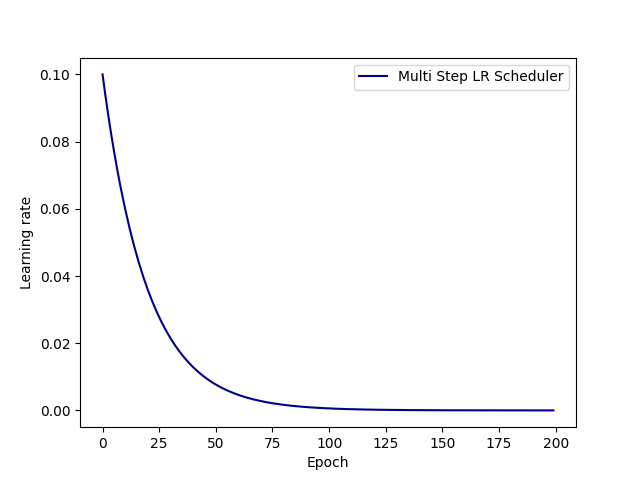
3. 指数学习率衰减（ExponentialLR）

每个训练周期（epoch）都将学习率乘以一个固定的衰减因子。

数学公式：

\[\eta_t = \eta_0 \times \gamma^t \]

其中 \(t\) 是当前 epoch 数。

PyTorch实现：

# 指数学习率衰减
# 调整方式：lr = lr * gamma^epoch，每个epoch都衰减
scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.95)

特点：

学习率平滑下降
衰减速度由 \(\gamma\) 控制：\(\gamma\) 越接近1，衰减越慢；越接近0，衰减越快
可能导致学习率过早变得过小

myplot4

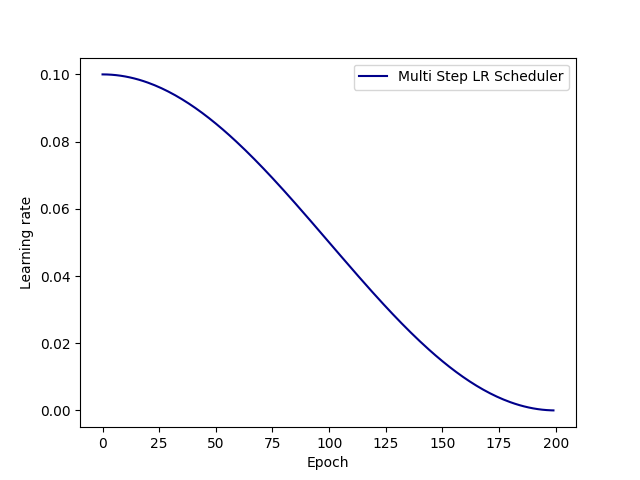
4. 余弦学习率衰减（CosineAnnealingLR）

按照余弦函数的形状调整学习率，从初始值衰减到最小值。

数学公式：

\[\eta_t = \eta_{\text{min}} + \frac{1}{2}(\eta_0 - \eta_{\text{min}}) \left(1 + \cos\left(\frac{t}{T_{\text{max}}} \pi\right)\right) \]

其中：

\(\eta_{\text{min}}\) 是学习率的最小值
\(T_{\text{max}}\) 是余弦周期的长度（总 epoch 数或半个周期）

PyTorch实现：

# 余弦学习率衰减
# 调整方式：lr = eta_min + (initial_lr - eta_min) * (1 + cos(pi * epoch / T_max)) / 2
scheduler_lr = optim.lr_scheduler.CosineAnnealingLR(
    optimizer, 
    T_max=max_epoch, 
    eta_min=0
)

特点：

学习率平滑下降，符合训练过程的自然规律
在训练后期学习率会非常小，有利于精细调优
通常能获得更好的最终精度

myplot5

5. 其他常用学习率衰减策略

余弦退火重启（CosineAnnealingWarmRestarts）

在余弦衰减的基础上，周期性地重启学习率，帮助跳出局部最优。

scheduler = optim.lr_scheduler.CosineAnnealingWarmRestarts(
    optimizer, 
    T_0=50,  # 初始重启周期
    T_mult=2,  # 周期倍增因子
    eta_min=0.001
)

按需调整学习率（ReduceLROnPlateau）

当验证集指标不再提升时降低学习率。

scheduler = optim.lr_scheduler.ReduceLROnPlateau(
    optimizer, 
    mode='min',  # 监控指标的模式：'min'表示越小越好，'max'表示越大越好
    factor=0.1,  # 衰减因子
    patience=10,  # 容忍多少个epoch指标没有改善
    verbose=True  # 打印衰减信息
)
# 使用方式：每个epoch后调用scheduler.step(val_loss)

代码示例

def demo():
    # 0.参数初始化
    LR = 0.1  # 设置学习率初始化值为0.1
    iteration = 10
    max_epoch = 200
    # 1 初始化参数
    y_true = torch.tensor([0])
    x = torch.tensor([1.0])
    w = torch.tensor([1.0], requires_grad=True)
    # 2.优化器
    optimizer = optim.SGD([w], lr=LR, momentum=0.9)
    # 3.设置学习率下降策略
    gamma = 0.95
    # 等间隔生成学习率衰减
    # 调整方式：lr = lr * gamma
    # scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=gamma)

    # 指定间隔学习率衰减
    # 调整方式：lr = lr * gamma
    # scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=[50, 125, 160], gamma=gamma)

    # 指数学习率衰减
    # 调整方式：lr= lr∗ gamma ^ epoch
    # scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)

    # 余弦学习率衰减
    # 调整方式：lr = eta_min + (initial_lr - eta_min) * (1 + cos(pi * T_cur / T_max)) / 2
    scheduler_lr = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=max_epoch, eta_min=0)

    # 4.获取学习率的值和当前的epoch
    lr_list, epoch_list = list(), list()
    for epoch in range(max_epoch):
        lr_list.append(scheduler_lr.get_last_lr())
        epoch_list.append(epoch)
        for i in range(iteration):  # 遍历每一个batch数据
            loss = ((w*x-y_true)**2)/2.0
            optimizer.zero_grad()
            # 反向传播
            loss.backward()
            optimizer.step()
        # 更新下一个epoch的学习率
        scheduler_lr.step()
    # 5.绘制学习率变化的曲线
    plt.plot(epoch_list, lr_list, label="Multi Step LR Scheduler",color="darkblue")
    plt.xlabel("Epoch")
    plt.ylabel("Learning rate")
    plt.legend()
    plt.show()

正则化

在设计机器学习算法时，我们希望模型在新样本上的泛化能力强。许多机器学习算法都采用相关策略来减小测试误差，这些策略统称为正则化（Regularization）。

神经网络具有强大的表示能力，但容易遇到过拟合问题，因此需要使用不同形式的正则化策略。

Dropout正则化

Dropout 是一种在训练过程中随机"丢弃"（失活）部分神经元的正则化技术。其核心思想是：在每次训练迭代中，随机选择一部分神经元不参与前向传播和反向传播，从而防止神经元之间的过度依赖，提高模型的泛化能力。
在训练阶段中

随机失活：每个神经元以超参数 \(p\) 的概率被保留，以 \(1-p\) 的概率被丢弃（输出置为0）
缩放操作：未被丢弃的神经元需要乘以缩放因子 \(\frac{1}{1-p}\)，以保持训练和测试阶段输出的期望值一致

在测试阶段中

所有神经元都参与计算，不进行随机丢弃
为了与训练阶段保持一致，通常需要将输出乘以 \(p\)（或权重乘以 \(p\)）

设第 \(l\) 层的输入为 \(x^{(l)}\)，权重为 \(W^{(l)}\)，偏置为 \(b^{(l)}\)，激活函数为 \(f\)。

训练阶段：

生成伯努利掩码 \(r^{(l)} \sim \text{Bernoulli}(p)\)
应用掩码：\(\tilde{x}^{(l)} = r^{(l)} \odot x^{(l)}\)
缩放：\(\tilde{x}^{(l)} = \frac{1}{1-p} \tilde{x}^{(l)}\)
计算输出：\(z^{(l+1)} = W^{(l+1)} \tilde{x}^{(l)} + b^{(l+1)}\)
激活：\(x^{(l+1)} = f(z^{(l+1)})\)

测试阶段：

直接计算：\(z^{(l+1)} = W^{(l+1)} x^{(l)} + b^{(l+1)}\)
激活：\(x^{(l+1)} = f(z^{(l+1)})\)

dropout = nn.Dropout(p=0.5)  # 定义 Dropout 层，丢弃概率为 0.5，一般在 0.2 - 0.5

批量归一化（Batch Normalization）

批量归一化通过对每一层神经网络的输入进行标准化处理（均值为0，方差为1），使得输入分布更加稳定，从而加速训练过程，提高模型性能。

批量归一化通常插入在全连接层或卷积层之后，激活函数之前：

原始结构：全连接层/卷积层 → 激活函数
批量归一化结构：全连接层/卷积层 → 批量归一化 → 激活函数

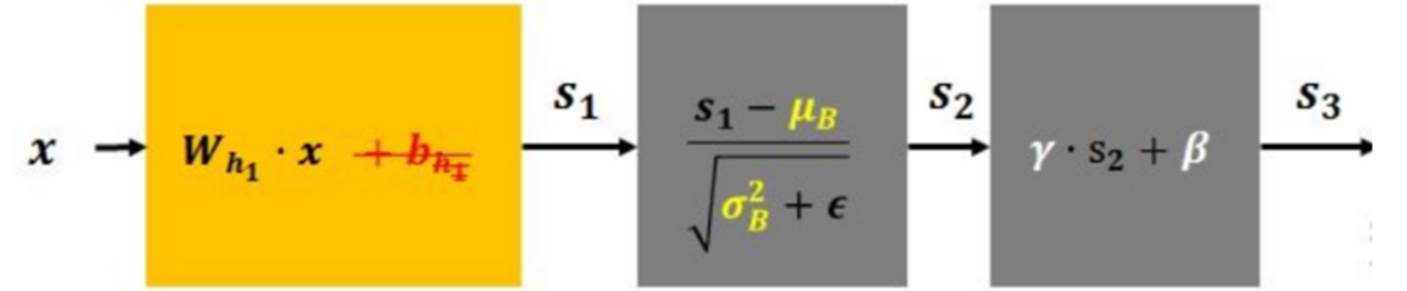
批量归一化对每个小批量（mini-batch）数据执行以下操作：

计算均值和方差：

\[\mu_B = \frac{1}{m} \sum_{i=1}^m x_i \]
\[\sigma_B^2 = \frac{1}{m} \sum_{i=1}^m (x_i - \mu_B)^2 \]
标准化：

\[\hat{x}_i = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \]
缩放和平移：

\[y_i = \gamma \hat{x}_i + \beta \]

其中：

\(B = \{x_1, x_2, ..., x_m\}\) 是一个小批量数据
\(\mu_B\) 是小批量数据的均值
\(\sigma_B^2\) 是小批量数据的方差
\(\epsilon\) 是一个很小的常数（通常为 \(10^{-5}\)），防止分母为零
\(\gamma\)（缩放参数）和 \(\beta\)（平移参数）是可学习的参数
\(y_i\) 是批量归一化的输出

# BatchNorm2d 的参数说明
nn.BatchNorm2d(
    num_features,      # 特征维度（通道数）
    eps=1e-05,         # 防止除零的小常数
    momentum=0.1,      # 运行均值/方差的动量
    affine=True,       # 是否学习γ和β参数
    track_running_stats=True  # 是否跟踪运行统计量
)

# 各种归一化方法的比较
batch_norm = nn.BatchNorm2d(64)      # 批量归一化
layer_norm = nn.LayerNorm(64)        # 层归一化, 对单个样本的所有特征进行归一化
instance_norm = nn.InstanceNorm2d(64) # 实例归一化, 对每个样本的每个通道单独归一化
group_norm = nn.GroupNorm(8, 64)      # 组归一化（8组）, 将通道分组后进行归一化

posted @ 2026-01-10 17:33 xggx 阅读(4) 评论(0) 收藏举报

刷新页面返回顶部

xggx

学习率衰减优化 和 正则化

学习率衰减优化 和 正则化