梯度下降优化算法

梯度下降优化算法

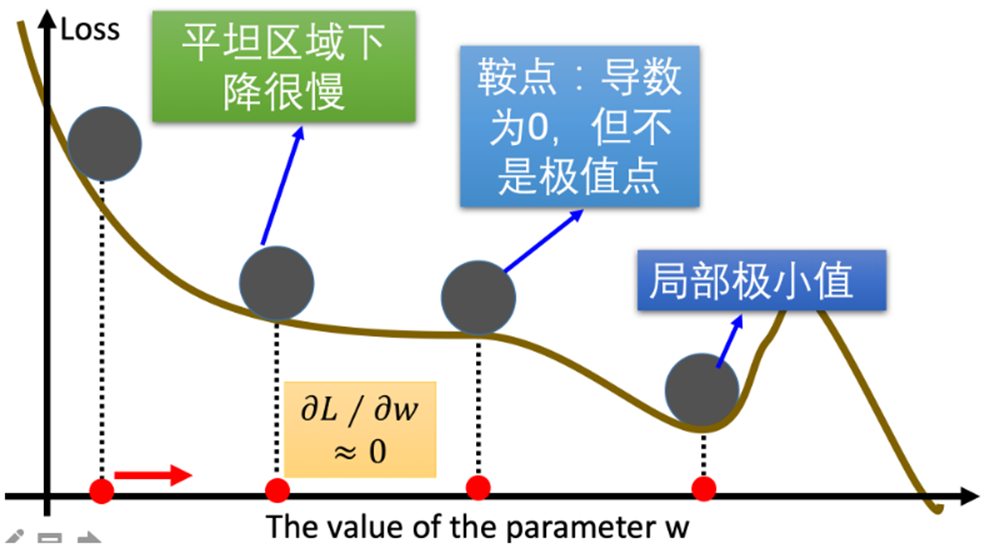
在梯度下降优化算法中，可能会遇到以下情况：

1. 遇到平缓区域，梯度值较小，参数优化变慢
2. 遇到"鞍点"，梯度为0，参数无法继续优化
3. 遇到局部最小值，参数无法达到全局最优

为了解决这些问题，研究者们提出了一系列梯度下降优化算法的改进方法，例如：Momentum、AdaGrad、RMSProp、Adam等。

指数移动加权平均

指数移动加权平均是一种计算平均值的方法，它考虑所有历史数值，但赋予不同时间点数据不同的权重：距离当前时间越远的数据权重越小，距离越近的数据权重越大。

例如：预测明天的气温时，今天的气温影响最大，一周前的气温影响较小，一个月前的气温影响更小。

计算公式可以用下面的式子来表示：

\[S_t = \begin{cases} Y_1, & t=0\\ \beta ×S_{t-1}+(1-\beta)×Y_t, & t>0 \end{cases} \]

其中：

• \(S_t\) 表示第 \(t\) 时刻的指数加权平均值
• \(Y_t\) 表示第 \(t\) 时刻的实际值
• \(\beta\) 是权重系数（0 < \(\beta\) < 1），\(\beta\) 值越大，平均值曲线越平缓

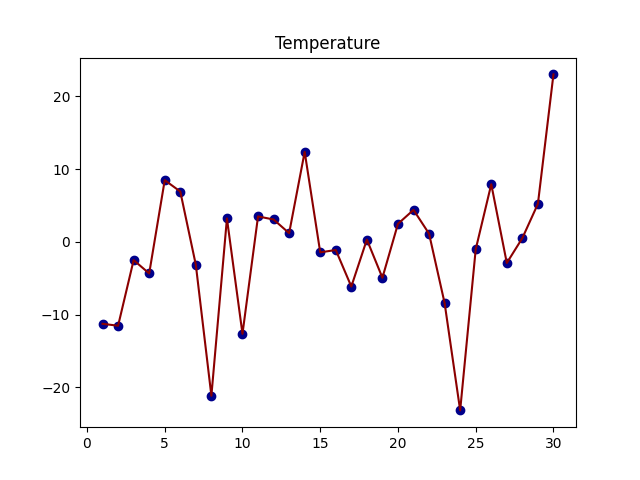
下面通过代码来看结果，随机产生 30 天的气温数据：

import torch
import matplotlib.pyplot as plt

ELEMENT_NUMBER = 30
# 1. 实际平均温度
def test01():
    # 固定随机数种子
    torch.manual_seed(0)
    # 产生30天的随机温度
    temperature = torch.randn(size=[ELEMENT_NUMBER,]) * 10
    print(temperature)
    # 绘制平均温度
    days = torch.arange(1, ELEMENT_NUMBER + 1, 1)
    plt.plot(days, temperature, color='darkred')
    plt.scatter(days, temperature, color='darkblue')
    plt.title('Temperature')
    plt.show()

# 2. 指数加权平均温度
def test02(beta):
    torch.manual_seed(0) # 固定随机数种子
    temperature = torch.randn(size=[ELEMENT_NUMBER,]) * 10 # 产生30天的随机温度
    exp_weight_avg = []
    for idx, temp in enumerate(temperature, 1):  # 从下标1开始
        # 第一个元素的的 EWA 值等于自身
        if idx == 1:
            exp_weight_avg.append(temp)
            continue
        # 第二个元素的 EWA 值等于上一个 EWA 乘以 β + 当前气温乘以 (1-β)
        new_temp = beta * exp_weight_avg[-1] + (1 - beta) * temp
        exp_weight_avg.append(new_temp)
    days = torch.arange(1, ELEMENT_NUMBER + 1, 1)
    plt.plot(days, exp_weight_avg, color='darkred')
    plt.scatter(days, temperature, color='darkblue')
    plt.title(f'Exponential Weighted Average Temperature (beta={beta})')
    plt.show()

if __name__ == '__main__':
    test01()
    test02(beta=0.5)
    test02(beta=0.9)

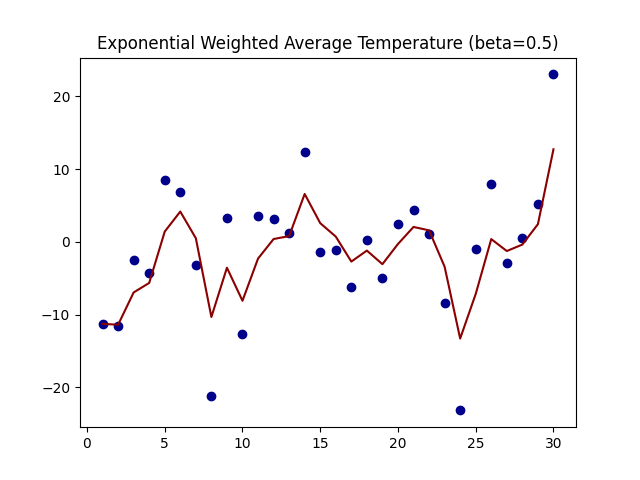
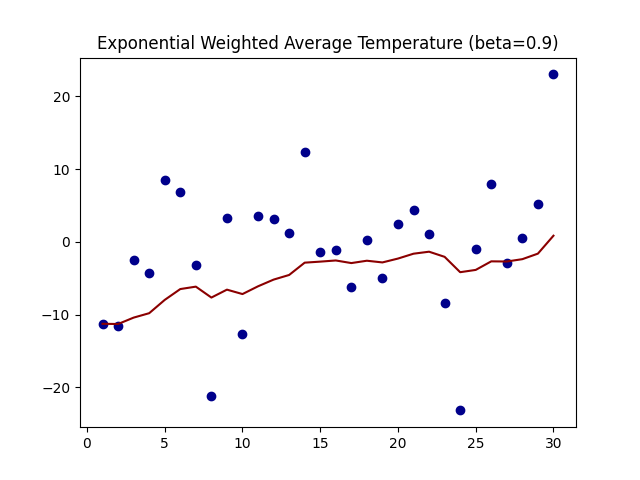
上图是β为0.5和0.9时的结果，从中可以看出：

• 指数加权平均绘制出的气温变化曲线更加平缓，

• β 的值越大，则绘制出的折线越加平缓，波动越小。(1-β越小,t时刻的St越不依赖Yt的值)

• β 值一般默认都是 0.9

Momentum（动量法）

Momentum算法通过引入"动量"的概念，加速梯度下降过程，并减少震荡。它借鉴了物理中动量的思想：当一个小球从山顶滚下时，速度会越来越快，动量会越来越大。

梯度计算公式：

\[s_t = \beta s_{t-1} + (1 - \beta) g_t \]

参数更新公式：

\[w_t = w_{t-1} - \eta s_t \]

其中：

• \(s_t\) 是当前时刻的指数加权平均梯度（动量）
• \(s_{t-1}\) 是历史指数加权平均梯度
• \(g_t\) 是当前时刻的梯度值
• \(\beta\) 是动量系数，通常取0.9或0.99
• \(\eta\) 是学习率
• \(w_t\) 是当前时刻的模型参数

Momentum如何克服优化问题

1. 克服鞍点问题：当处于鞍点时，当前梯度为0，普通梯度下降会停滞。但Momentum已经积累了历史梯度动量，可能帮助参数越过鞍点。

2. 减少震荡：Mini-batch梯度下降中，不同batch的梯度方向可能不一致，导致震荡。Momentum通过指数加权平均平滑了梯度方向，使优化路径更加稳定。

3. 加速收敛：在平缓区域，虽然当前梯度很小，但动量仍能保持一定的更新速度。

w = torch.tensor([1.0], requires_grad=True)
loss = ((w ** 2) / 2.0).sum()

# momentum
optimizer = torch.optim.SGD([w], lr=0.01, momentum=0.9)

optimizer.zero_grad()
loss.backward()
optimizer.step()

AdaGrad（自适应梯度算法）

AdaGrad算法为每个参数分量自适应地调整学习率：对频繁更新的参数使用较小的学习率，对不频繁更新的参数使用较大的学习率。

算法步骤

1. 初始化学习率 \(\eta\)、参数 \(w\)、小常数 \(\epsilon = 10^{-10}\)
2. 初始化梯度累计变量 \(r = 0\)
3. 从训练集中采样一个小批量，计算梯度 \(g_t\)
4. 累积平方梯度：\(r_t = r_{t-1} + g_t \odot g_t\)（\(\odot\) 表示逐元素相乘）
5. 计算自适应学习率：\(\eta_t = \frac{\eta}{\sqrt{r_t} + \epsilon}\)
6. 更新参数：\(w_t = w_{t-1} - \eta_t \odot g_t\)
7. 重复步骤3-6

梯度平方累积：

\[r_t = r_{t-1} + g_t \odot g_t \]

参数更新：

\[w_t = w_{t-1} - \frac{\eta}{\sqrt{r_t} + \epsilon} \odot g_t \]

• 优点：自适应学习率，适合处理稀疏数据
• 缺点：随着训练进行，\(r_t\) 会持续累积增大，导致学习率过早、过量降低，后期可能因学习率过小而无法收敛到最优解

optimizer = torch.optim.Adagrad([w], lr=0.01)

RMSProp（均方根传播）

RMSProp是对AdaGrad的改进，使用指数加权平均代替历史梯度平方的累积和，解决了AdaGrad学习率持续下降的问题。

算法步骤

1. 初始化学习率 \(\eta\)、参数 \(w\)、小常数 \(\epsilon = 10^{-10}\)
2. 初始化梯度累计变量 \(r = 0\)
3. 从训练集中采样一个小批量，计算梯度 \(g_t\)
4. 计算指数加权平均梯度平方：\(r_t = \beta r_{t-1} + (1 - \beta) g_t \odot g_t\)
5. 计算自适应学习率：\(\eta_t = \frac{\eta}{\sqrt{r_t} + \epsilon}\)
6. 更新参数：\(w_t = w_{t-1} - \eta_t \odot g_t\)
7. 重复步骤3-6

指数加权平均梯度平方：

\[r_t = \beta r_{t-1} + (1 - \beta) g_t \odot g_t \]

参数更新：

\[w_t = w_{t-1} - \frac{\eta}{\sqrt{r_t} + \epsilon} \odot g_t \]

其中 \(\beta\) 通常取0.9。

RMSProp的特点:

• 解决了AdaGrad学习率持续下降的问题
• 在非凸优化问题上表现良好
• 是许多深度学习框架的默认优化器之一

optimizer = torch.optim.RMSprop([w], lr=0.01, alpha=0.9)

Adam（自适应矩估计）

Adam算法结合了Momentum和RMSProp的优点，同时计算梯度的一阶矩（均值）和二阶矩（方差），并进行偏差校正。

算法原理

Adam包含两个核心思想：

1. 修正梯度：使用梯度的指数加权平均（一阶矩），类似Momentum
2. 修正学习率：使用梯度平方的指数加权平均（二阶矩），类似RMSProp

一阶矩估计（梯度均值）：

\[m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t \]

二阶矩估计（梯度平方的均值）：

\[v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t \odot g_t \]

偏差校正（解决初始阶段估计偏差）：

\[\hat{m}_t = \frac{m_t}{1 - \beta_1^t} \]

\[\hat{v}_t = \frac{v_t}{1 - \beta_2^t} \]

参数更新：

\[w_t = w_{t-1} - {\hat{m}_t} \cdot \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \]

其中：

• \(\beta_1\) 和 \(\beta_2\) 是衰减率，通常取0.9和0.999
• \(\epsilon\) 是小常数，防止除零，通常取 \(10^{-8}\)
• \(\eta\) 是学习率

Adam的特点：

• 结合了Momentum和RMSProp的优点
• 自适应调整每个参数的学习率
• 偏差校正使初始阶段更新更稳定
• 通常作为默认优化器，在许多任务上表现良好

optimizer = torch.optim.Adam([w], lr=0.01)

优化算法对比

算法	核心思想	优点	缺点	适用场景
SGD	基础梯度下降	简单，理论成熟	易陷入局部最优，收敛慢	基础模型
Momentum	引入动量	加速收敛，减少震荡	需要调节动量参数	深度网络训练
AdaGrad	自适应学习率	适合稀疏数据	学习率持续下降	稀疏特征学习
RMSProp	指数加权平均梯度平方	解决AdaGrad学习率下降问题	需要调节衰减率	非凸优化问题
Adam	结合Momentum和RMSProp	自适应学习率，收敛快	可能不如SGD泛化好	大多数深度学习任务

选择优化器的建议

1. Adam通常是首选的优化器，因为它结合了多种优点且超参数相对鲁棒
2. 对于需要更好泛化性能的任务，可以尝试使用SGD+Momentum
3. RMSProp在循环神经网络中表现良好
4. 对于稀疏数据，AdaGrad或其变体可能更合适
5. 实际应用中需要通过实验选择最适合特定任务的优化器