神经网络基础

构建神经网络

神经网络是由多个神经元组成，构建神经网络就是在构建神经元。以下是神经网络中神经元的构建说明：

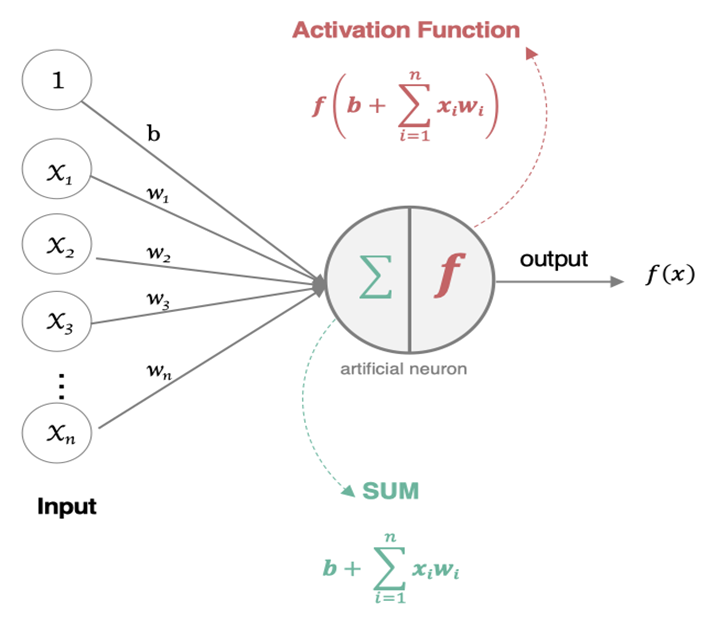
接下来，我们使用多个神经元来构建神经网络，相邻层之间的神经元相互连接，并给每一个连接分配一个强度，如下图所示：

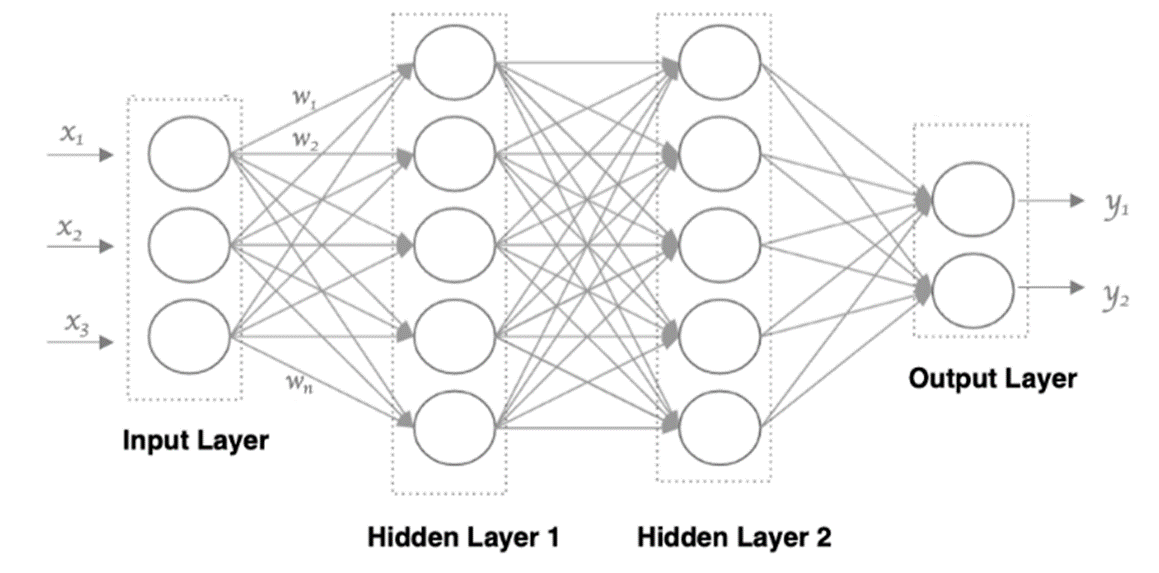
神经网络中信息只向一个方向移动，即从输入节点向前移动，通过隐藏节点，再向输出节点移动。其中的基本部分是:

输入层：接收原始数据（如图像像素、文本特征等）。每个输入特征对应一个神经元，该层不对数据做处理，仅负责传递。
隐藏层：位于输入与输出层之间，是网络进行特征提取和变换的核心。“深度”通常由隐藏层的数量决定。
输出层：产生网络的最终预测结果（如分类概率、回归值等）。其设计取决于任务类型。

在全连接神经网络中：

同一层的神经元之间没有连接。
第 N 层的每个神经元都与第 N-1 层的所有神经元相连。
连接具有可学习的权重（w）和偏置（b），信息通过“加权求和 → 加偏置 → 激活函数”的方式向前传递。
网络接收的输入数据必须是二维的（如 [batch_size, features]），且在层间以二维形式流动。

如下图是神经网络内部状态值和激活值

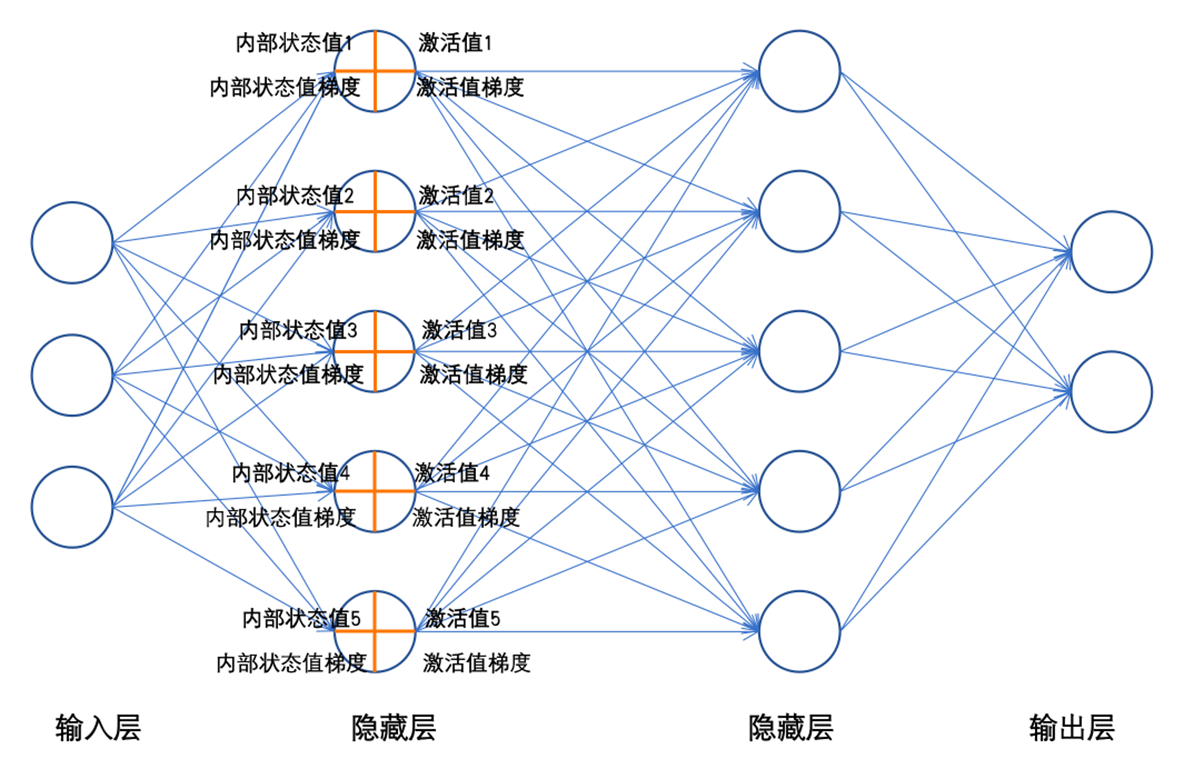
激活函数

激活函数为神经网络引入了非线性，使其能够拟合复杂的函数关系。没有它，多层网络将退化为单层线性模型。

1. sigmoid

激活函数公式：

\[f(x) = \frac{1}{1 + e^{-x}} \]

激活函数求导公式：

\[f'(x) = \frac{e^{-x}}{(1 + e^{-x})^2}= f(x) \cdot (1 - f(x)) \]

sigmoid 激活函数的函数图像如下:

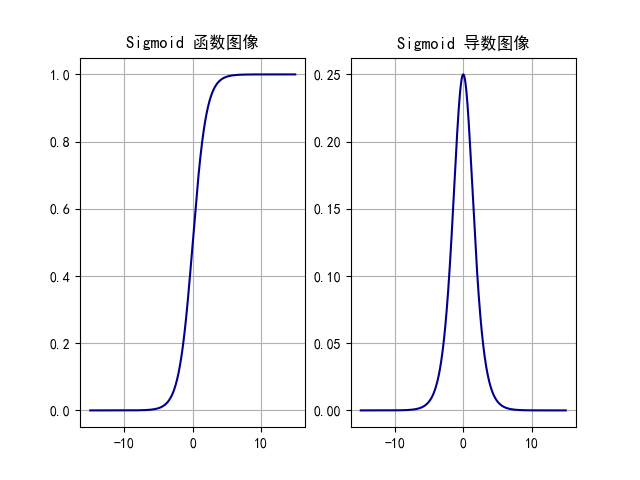
sigmoid

特点：

sigmoid 函数可以将任意的输入映射到 (0, 1) 之间，当输入的值大致在 < -6 或者 > 6 时，意味着输入任何值得到的激活值都是差不多的，这样会丢失部分的信息。比如：输入 100 和输出 10000 经过 sigmoid 的激活值几乎都是等于 1 的，但是输入的数据之间相差 100 倍的信息就丢失了。
对于 sigmoid 函数而言，输入值在 [-6, 6] 之间输出值才会有明显差异，输入值在 [-3, 3] 之间才会有比较好的效果。
通过上述导数图像，我们发现导数数值范围是 (0, 0.25)，当输入 <-6 或者 >6 时，sigmoid 激活函数图像的导数接近为 0，此时网络参数将更新极其缓慢，或者无法更新。
一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象（即梯度值很小, 接近0，w(新)=w(旧)-学习率×梯度）。而且，该激活函数并不是以 0 为中心的，所以在实践中这种激活函数使用的很少。sigmoid函数一般只用于二分类的输出层。

_, axes = plt.subplots(1, 2)

# 函数图像
x = torch.linspace(-15, 15, 1000) 
y = torch.sigmoid(x) # 输入值x通过sigmoid函数转换成激活值y
axes[0].plot(x, y, color='darkblue')

# 导数图像
x = torch.linspace(-15, 15, 1000, requires_grad=True)
y = torch.sigmoid(x)
y.sum().backward()
# x.detach():输入值x的数值    x.grad:计算梯度，求导
axes[1].plot(x.detach(), x.grad, color='darkblue')

2. tanh

Tanh 的公式如下：

\[f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}= \frac{e^{2x} - 1}{e^{2x} + 1} \]

激活函数求导公式:

\[f'(x) = (\frac{e^x - e^{-x}}{e^x + e^{-x}})' = \frac{4}{(e^x + e^{-x})^2} = 1 - f^2(x) \]

Tanh 的函数图像、导数图像如下：

tanh

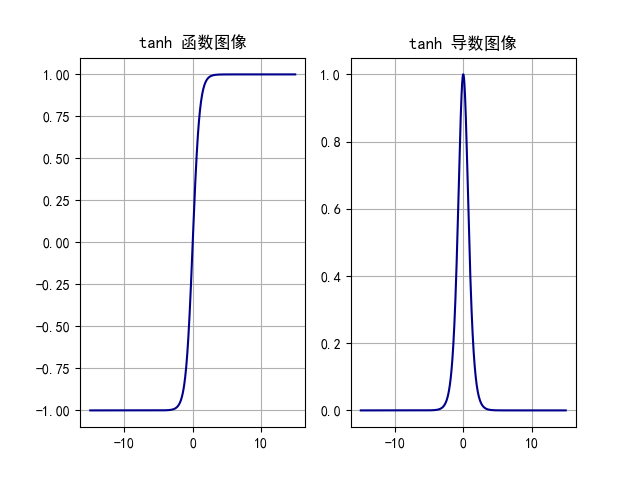
特点：

Tanh 函数将输入映射到 (-1, 1) 之间，图像以 0 为中心，在 0 点对称，当输入大概 < -3 或者 > 3 时将被映射为 -1 或者 1。其导数值范围 (0, 1)，当输入的值大概 <-3 或者 > 3 时，其导数近似 0。
与 Sigmoid 相比，它是以 0 为中心的，且梯度相对于sigmoid大，使得其收敛速度要比 Sigmoid 快，减少迭代次数。然而，从图中可以看出，Tanh 两侧的导数也为 0，同样会造成梯度消失。
若使用时可在隐藏层使用tanh函数,且适用于浅层神经网络（不超过5层），在输出层使用sigmoid函数。

# 函数图像
x = torch.linspace(-15, 15, 1000)
y = torch.tanh(x) # 输入值x通过tanh函数转换成激活值y
axes[0].plot(x, y, color='darkblue')

# 导数图像
x = torch.linspace(-15, 15, 1000, requires_grad=True)
y = torch.tanh(x)
y.sum().backward()
# x.detach():输入值x的数值  x.grad:计算梯度，求导
axes[1].plot(x.detach(), x.grad, color='darkblue')

3. Relu

ReLU 公式如下：

\[f(x)=\max(0,x) \]

ReLU求导公式:

\[f'(x)=0\ or \ 1 \]

ReLU

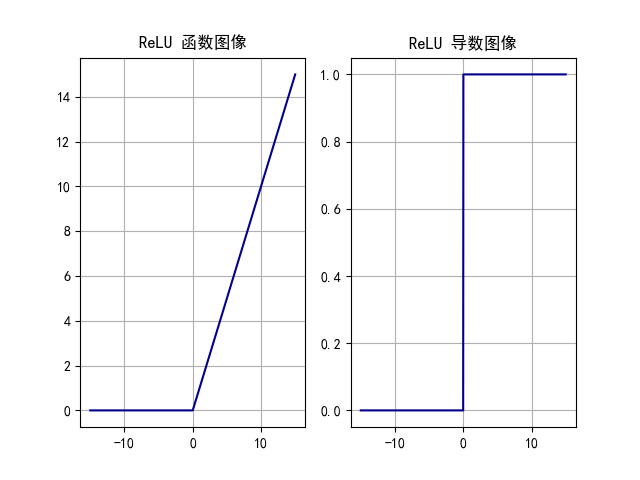
特点：

•ReLU 激活函数将小于 0 的值映射为 0，而大于 0 的值则保持不变，它更加重视正信号，而忽略负信号，这种激活函数运算更为简单，能够提高模型的训练效率。默认情况下 ReLU 只考虑正样本，可以使用 LeakyReLU , PReLU 来考虑正负样本

•当 x < 0 时，ReLU 导数为 0，而当 x > 0时，则不存在饱和问题。所以，ReLU 能够在 x > 0 时保持梯度不衰减，从而缓解梯度消失问题。然而，随着训练的推进，部分输入会落入小于 0 区域，导致对应权重无法更新。这种现象被称为“神经元死亡”。

•ReLU 是目前最常用的激活函数。与 sigmoid 相比，ReLU 的优势是：采用 sigmoid 函数，计算量大（指数运算），反向传播求误差梯度时，计算量相对大，而采用 Relu 激活函数，整个过程的计算量节省很多。 sigmoid 函数反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。 Relu 会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生。

# 函数图像
x = torch.linspace(-15, 15, 1000)
y = torch.relu(x) # 输入值x通过ReLU函数转换成激活值y
axes[0].plot(x, y, color='darkblue')

# 导数图像
x = torch.linspace(-15, 15, 1000, requires_grad=True)
y = torch.relu(x)
y.sum().backward()
# x.detach():输入值x的数值  x.grad:计算梯度，求导
axes[1].plot(x.detach(), x.grad, color='darkblue')

4. Softmax

softmax用于多分类过程中，它是二分类函数sigmoid在多分类上的推广，目的是将多分类的结果以概率的形式展现出来, 二元分类时退化为 Sigmoid）。计算方法如下：

\[softmax({z_i}) = \frac{e^{z_i}}{\sum_{j=1}^{K} e^{z_j}} \]

\[softmax(z_1) = \frac{1}{1 + e^{-(z_1 - z_2)}} ,\ K=2 \]

Softmax 就是将网络输出的 logits 通过 softmax 函数，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们将它理解成概率，选取概率最大（也就是值对应最大的）节点，作为我们的预测目标类别。

其他激活函数

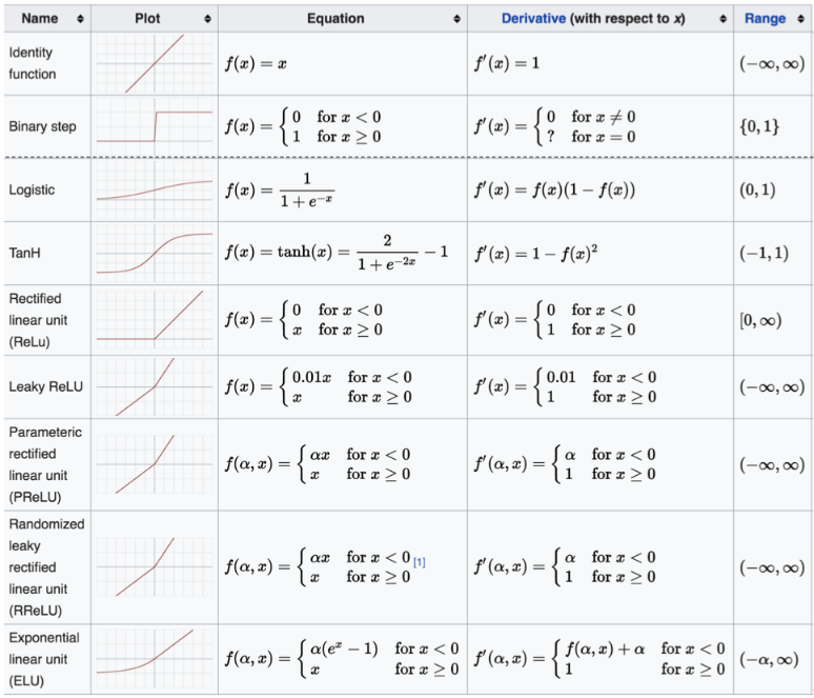
对于隐藏层：

首选 ReLU，因其计算快、收敛好。
若 ReLU 效果不佳（如出现大量死亡神经元），可尝试其变体 Leaky ReLU 或 PReLU。
慎用 Sigmoid，因其易导致梯度消失。
Tanh 可用于浅层网络的隐藏层。

对于输出层：

二分类：使用 Sigmoid。
多分类：使用 Softmax。
回归：通常使用线性激活（即恒等函数 f(x)=x）。

参数初始化

参数初始化的作用

1. 防止梯度消失或爆炸：初始权重值过大或过小会导致梯度在反向传播中指数级增大或缩小。

2. 提高收敛速度：合理的初始化使得网络的激活值分布适中，有助于梯度高效更新。

3. 保持对称性破除：权重的初始化需要打破对称性，否则网络的学习能力会受到限制。

基础 / 非适应性初始化

这类方法通常实现简单，但缺乏对网络结构的自适应调整，易引发训练问题。

方法	核心思想	优点	缺点	适用场景
全零初始化	所有权重初始化为0。	实现极其简单。	1. 对称性问题：所有神经元参数相同，更新一致，网络失去表达能力。 2. 梯度为零，无法进行有效学习。	几乎不用于权重。常用于将偏置项初始化为0。
全一初始化	所有权重初始化为1。	实现简单。	1. 对称性问题（同全零）。 2. 梯度爆炸：激活值在网络中指数级增长。	极少使用。主要用于临时测试或调试网络通路。
固定值初始化	所有权重初始化为某个固定常数。	实现简单，确定性。	1. 对称性问题（同全零）。 2. 权重设置不当易导致梯度消失或爆炸。	测试或调试，验证特定行为。
（简单）随机初始化	权重从一个简单的分布（如均匀分布、正态分布）中随机采样。	能有效打破对称性，使神经元开始分化。	分布范围（如方差）选择不当，在深层网络中极易导致梯度消失或爆炸。	浅层网络（如3层以内）。是更高级方法的基础。

适应性初始化

这类方法根据网络结构（输入/输出维度）自动调整初始权重的分布范围，旨在维持数据在前向和反向传播中的方差稳定。

方法	别名	核心思想与公式	优点	缺点	适用场景
Xavier 初始化	Glorot 初始化	设计目标是保持输入和输出的方差一致，适用于线性激活函数。均匀分布： \(W \sim U\left[-\frac{\sqrt{6}}{\sqrt{fan\_in + fan\_out}}, \frac{\sqrt{6}}{\sqrt{fan\_in + fan\_out}}\right]\) 正态分布： \(W \sim N\left(0, \sqrt{\frac{2}{fan\_in + fan\_out}}\right)\)	有效缓解使用 Sigmoid、Tanh 等饱和激活函数时的梯度消失问题。	对于 ReLU 及其变体等非对称、非饱和激活函数，效果欠佳，可能导致输出方差收缩。	使用 Sigmoid 或 Tanh 激活函数的网络。
Kaiming 初始化	He 初始化	专为 ReLU 家族设计。仅考虑正向传播时，ReLU会将一半的神经元置零，因此将方差放大一倍以进行补偿。均匀分布： \(W \sim U\left[-\frac{\sqrt{6}}{\sqrt{fan\_in}}, \frac{\sqrt{6}}{\sqrt{fan\_in}}\right]\) 正态分布： \(W \sim N\left(0, \sqrt{\frac{2}{fan\_in}}\right)\)	非常适合 ReLU、Leaky ReLU、PReLU 等激活函数，能在深层网络中保持梯度的稳定性。	对于 Sigmoid、Tanh 等饱和激活函数，初始权重可能过大，导致激活值饱和。	使用 ReLU 及其变体激活函数的深度网络（如CNN、现代Transformer）。

fan_in：当前层的输入维度，即来自上一层的神经元数量。
fan_out：当前层的输出维度，即传递给下一层的神经元数量。
对称性问题：若同一层所有神经元的初始权重完全相同，则在反向传播时它们的梯度也会相同，导致所有神经元学习到相同的特征，网络容量大幅下降。

代码样例

	linear = nn.Linear(5, 3)
    # 1. 随机初始化(均匀分布)
    nn.init.uniform_(linear.weight)

    # 2. 正态分布初始化
    nn.init.normal_(linear.weight, mean=0.0, std=1)

    # 3. kaiming正态分布初始化
    nn.init.kaiming_normal_(linear.weight, mode='fan_in', nonlinearity='relu')

    # 4. kaiming均匀分布初始化
    nn.init.kaiming_uniform_(linear.weight, mode='fan_in', nonlinearity='relu')

    # 5. xavier正态分布初始化
    nn.init.xavier_normal_(linear.weight)

    # 6. xavier均匀分布初始化
    nn.init.xavier_uniform_(linear.weight)

    # 7. 全零初始化
    nn.init.zeros_(linear.weight)

    # 8. 全一初始化
    nn.init.ones_(linear.weight)

    # 9. 固定值初始化
    nn.init.constant_(linear.weight, 0.5)

    print(linear.weight)
    print(linear.bias)

关于初始化的选择上

  1. 对于浅层网络，可以选择简单的初始化方法，如随机初始化或正态分布初始化。
  2. 对于深层网络
     kaiming初始化 ：适用于ReLU及其变体激活函数的网络。
     xavier初始化 ：适用于Sigmoid和Tanh激活函数的网络。