静态主席树

静态主席树

在了解主席树之前，你需要先了解前缀和与权值线段树。这里以HDOJ2665为例，来讲解静态主席树。题目是给定区间，问区间第k大数。

题意

首先对于一个区间，它的值域是一个集合，例如，给定数组\(a[10] = {1, 73 ,73 ,5 ,22, 4, 6, 22, 81, 0}\)，它的值域就是\(A={0,1, 4,5,6,22,73, 81}\)，可以看到这里涉及到去重和离散（离散就是把一串不连续的数据放在一个数组里，这样根据连续的下标来取值），对于一个已经离散化的数组，根据下标就能知道他代表的值，就是\(i\)与\(a[i]\)的关系，\(a[i]\)是初值。对于上述数组，我们想求1到73之间有多少个数，我们只需在离散后的数组二分查找到其下标，即求1到7（下标从1开始）之间有多少个。

题解

知道了离散的概念后，我们根据这个离散数组建一棵线段树，代表主席树的最初状态。下面以\([53,89,12,64]\)为例。

先建立一棵空树：

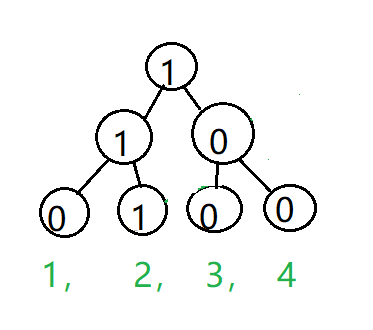
此时一个点都没插入，所有节点的值都为0。

下面就开始操作主席树了。首先按照原始数组的顺序插入值，第一个是53，在离散后的数组中可以发现他的下标是2。下面咱就再建一颗线段树。

空间复杂度分析

53在第二个下标处，所以[2,2]区间的数就+1，那么[1,2]的数也+1，那么[1,4]的数也+1，发现啥了没有，[3,4]和[1,1]根本没动。没动我还腾着这个空间干嘛？在之后每插入一个数，你都会发现很多节点都没更新，我们来算算，在给定的长度为n的初始数组，这么建要多少空间。

首先，根据线段树的结构你会发现，每一层的节点数都是2的幂，其中叶节点的数量不足2的幂也要补足。我们可以发现，叶节点的幂至多是\(k\log_2n+1\)，就代表就\(k\)层，用个等比数列求和公式求一下不难算出节点数为\(2^{k+1}-1\)个，带入n就是\(4n-1\)个，后面的一略去，\(n\)颗线段树就是\(4n^2\)个，这里\(n\)最大为\(1e^5\),则对最大空间数就是\(4e^{10}\)，这不MLE才怪。

考虑到上面有很多节点并没有更新，没更新代表这些点和之前的一颗线段树的这些节点是一致的。于是我们就考虑将这些信息共用，这样我们插入一个数时，就让第二颗线段树的左右孩子等于之前一个线段树的左右孩子的下标，哪个不一样，我们再开一个空间给他，这样空间利用率大大提升。我们发现，每次更新时，只更新了一条链，而链长就是层数，层数就是k+1，忽略常数，我们不难算出优化后的主席树的空间复杂度为\(4n+nlog_2n\)带入常数计算得最大节点数约为\(20n\)，空间复杂度大大减少。当然做题的时候可以开到\(n<<5\)，即\(32n\)。

模拟插入的操作

首先插入53，他在离散后的数组下标为2，那么\([3, 4]、[1,1]\)就直接用了，不用再开了。

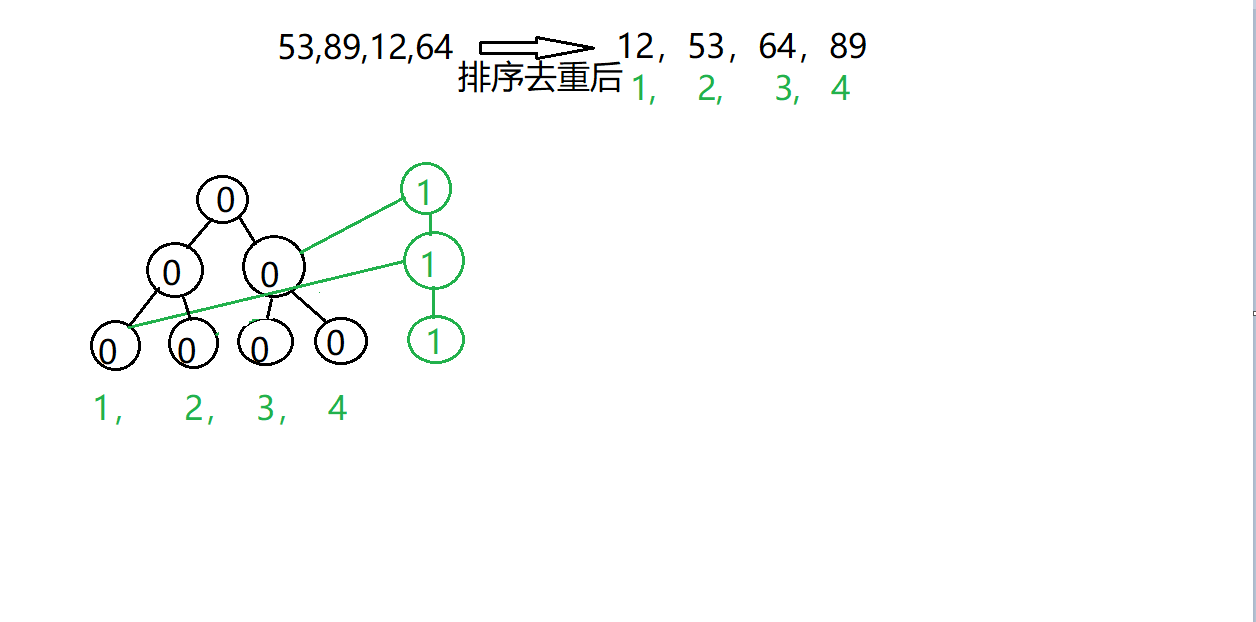
注意，绿色的这条链其实是它所对应根节点的左子树。

再插入89

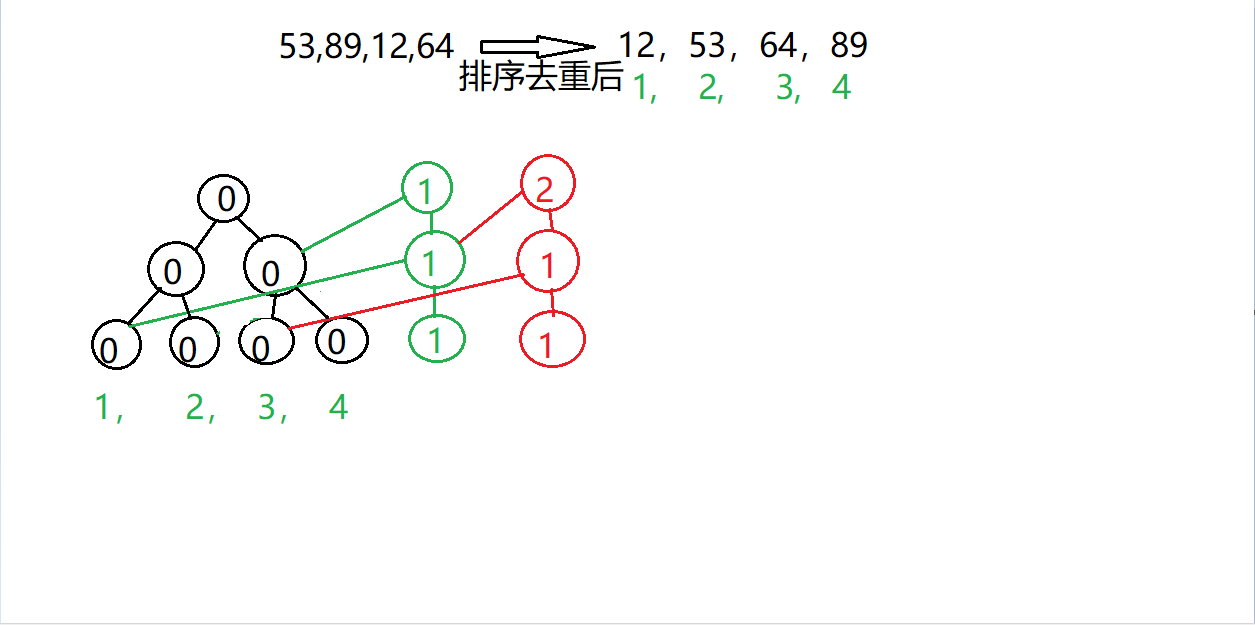
再插入12

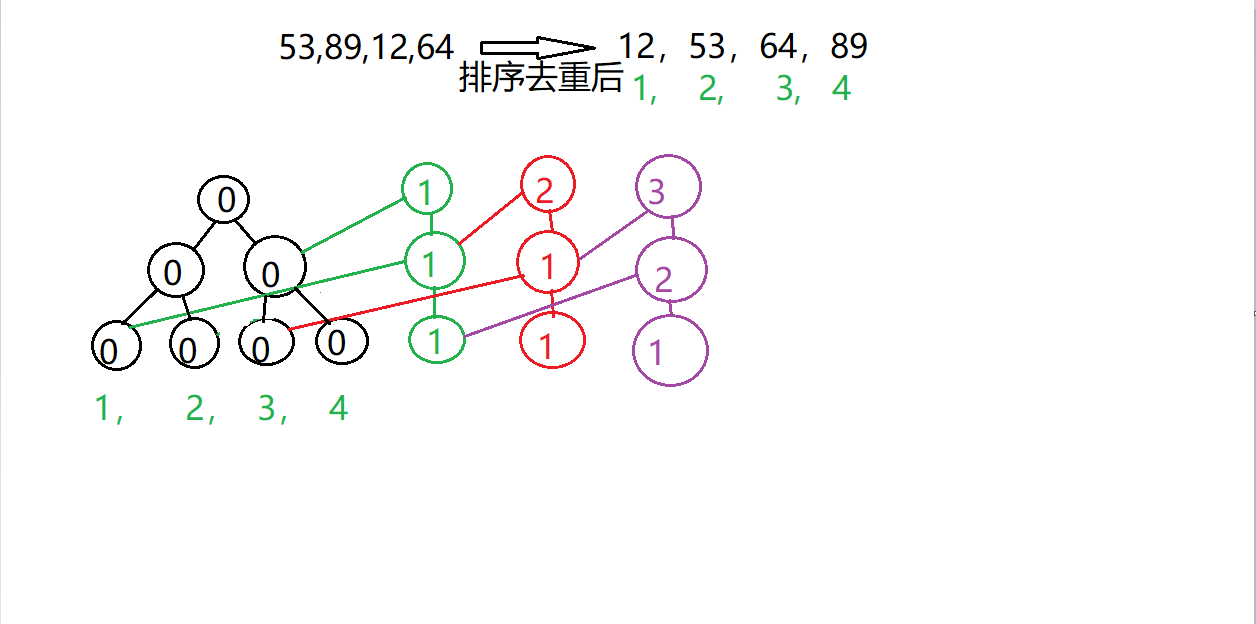
最后插入64

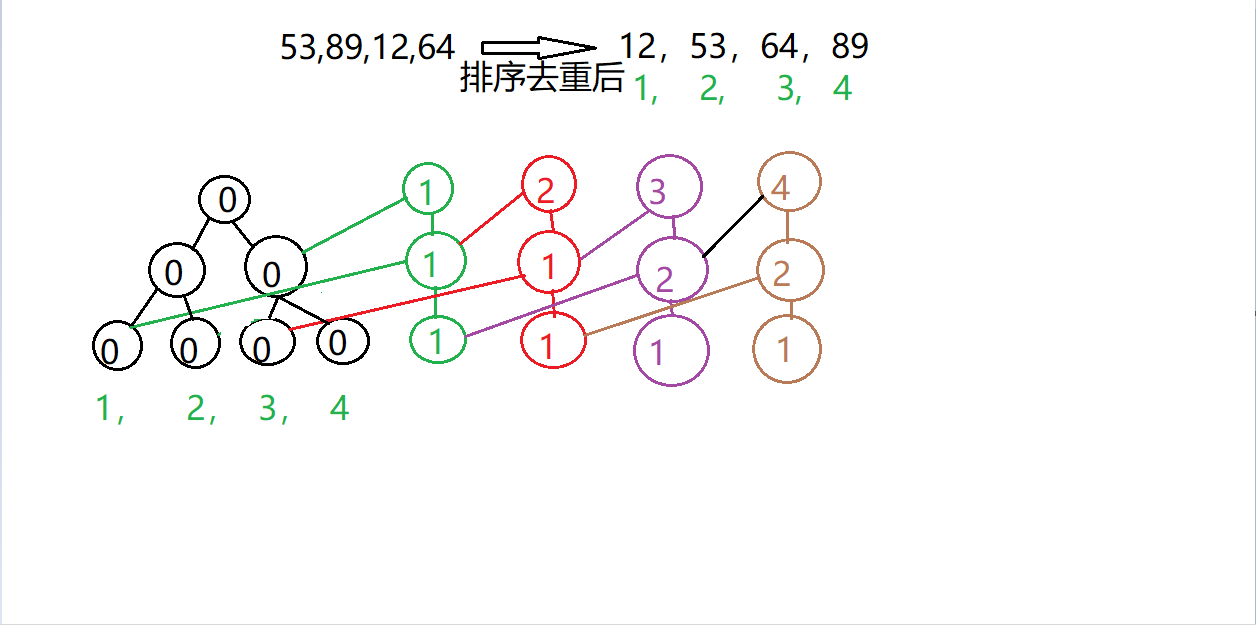
不妨模拟一遍，你会发现so easy~

以上都是更新操作，查询操作其实也很简单，我们上面维护的其实是一个前缀和，例如我们查询\([l, r]\)第\(k\)大数，我们先查询\([1, r]\)里数的个数，再查询\([1, l-1]\)里的个数，相减就是\([l, r]\)区间里的数，然后再在\([l, r]\)里进行查找。

AC代码

#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); ++i)
#define sc(a) scanf("%d", &a)
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 1e5 + 5;
const int maxm = maxn * 20;
/*
各个数组的用处:
val数组用来保存该节点的前缀和，ls数组用来保存该节点的左孩子，rs数组用来保存右孩子，root数组用来保存根节点的下标
a数组用来保存原式值（输入），b数组用来去重，去重完a数组就可以用作他用，保存别的值，tot代表当前结点总数
注意：开结构体会MLE
*/
int val[maxm], ls[maxm], rs[maxm], a[maxn], b[maxn], root[maxm], n, tot;
//建一棵空树
void build(int &node, int l, int r) {
    node = ++tot;   //注意建树顺序
    val[node] = 0;  //空树值为0
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(ls[node], l, mid);
    build(rs[node], mid + 1, r);
}
//插入值，每次插入则多加一条链，pre代表上次的根节点，pos代表插入的位置，node代表现在要更新的值
void update(int &node, int l, int r, int pre, int pos) {
    node = ++tot;   //每个节点都有对应的编号
    ls[node] = ls[pre]; //先让该节点的左右节点等于上个等位节点的左右孩子
    rs[node] = rs[pre];
    //更新的节点要+1
    val[node] = val[pre] + 1;
    if (l == r) return;
    int mid = (l + r) >> 1;
    if (pos <= mid) update(ls[node], l, mid, ls[pre], pos);
    else update(rs[node], mid + 1, r, rs[pre], pos);
}
int query(int st, int ed, int l, int r, int pos) {
    if (l == r) return l;
    int mid = (l + r) >> 1;
    //利用前缀和计算该区间内数的个数
    int cnt = val[ls[ed]] - val[ls[st]];
    //计算左孩子的前缀和，如果目标值小于它，则进入左子树。
    if (pos <= cnt) return query(ls[st], ls[ed], l, mid, pos);
    else return query(rs[st], rs[ed], mid + 1, r, pos - cnt);
}
signed main() {
    int kase; sc(kase);
    while (kase--) {
        int q; sc(n), sc(q);
        _for(i, 1, n) {
            sc(a[i]);
            b[i] = a[i];
        }

        //去重
        sort(b + 1, b + 1 + n);
        int num = unique(b + 1, b + 1 + n) - b - 1;

        tot = 0;
        build(root[0], 1, num);

        _for(i, 1, n) a[i] = lower_bound(b + 1, b + 1 + num, a[i]) - b; //找出这个数在离散后数组里位置,直接用a数组存
        _for(i, 1, n) update(root[i], 1, num, root[i - 1], a[i]);

        int x, y, z;
        while (q--) {
            sc(x), sc(y), sc(z);
            //找出该区间在离散后数组里的位置
            int ans = query(root[x - 1], root[y], 1, num, z);
            printf("%d\n", b[ans]);
        }
    }
    return 0;
}