树链剖分
树链剖分
什么是树链剖分
顾名思义,将一棵树分割为多个相对独立的链,以便于高效维护和处理树上的路径、子树等问题。
树链剖分有什么作用?
常用的树链剖分有重链剖分与长链剖分,这里主要介绍重链剖分。它常用于高效解决树上路径查询、子树查询、区间修改等问题,常与线段树等数据结构结合使用。
基本概念
重儿子:父节点所有儿子中子树大小最大的儿子
轻儿子:父节点所有儿子中除了重儿子的其他儿子
重边:父节点与其重儿子所连的边
轻边:父节点与其轻儿子所连的边
重链:重边所连成的链
轻链:轻边所连成的链
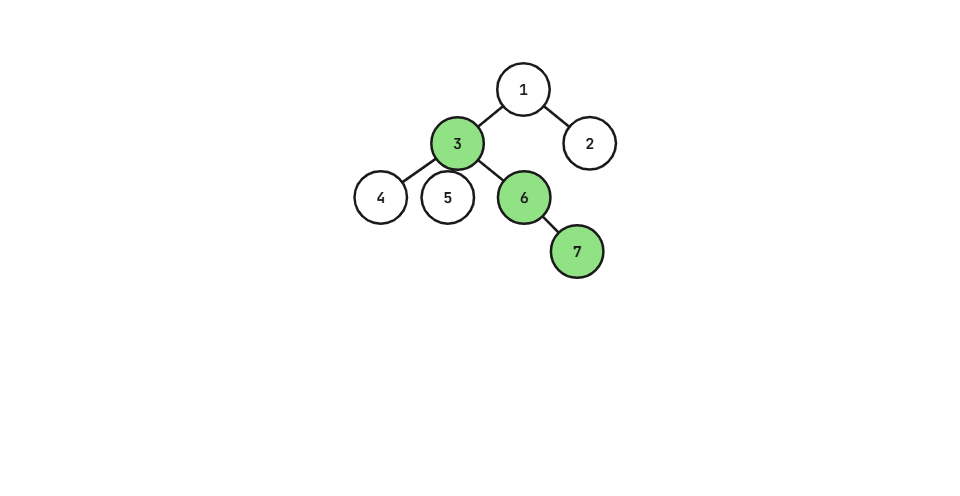
以这棵树为例,它的根节点是\(1\),节点\(2\)与节点\(3\)是它的子节点。我们可以注意到以节点\(3\)为根的子树大小为\(5\),显然大于以节点\(2\)为根的子树大小,所以节点\(3\)是节点\(1\)的重儿子。
同理,节点\(6\)是节点\(3\)的重儿子,节点\(7\)是节点\(6\)的重儿子。
节点\({1,3,6,7}\)构成了一条重链。
树链剖分求LCA的原理
树链剖分求最近公共祖先的核心思想是利用每个节点所在重链的顶端节点信息,将树上的两个节点不断跳到各自重链的顶端,并向上跳到父链,直到它们位于同一条重链上。此时,深度较小的节点即为LCA。
步骤如下:
-
比较两个节点所在重链的顶端节点,深度较大的节点跳到其重链顶端的父节点。
-
重复上述过程,直到两个节点在同一条重链上。
-
此时,深度较小的节点即为LCA。
这样,树链剖分可以在\(O(\log_2 n)\)时间内高效求解LCA问题。
每次跳链时,都会将深度较大的节点跳到其重链顶端的父节点。由于重链的定义是每次优先选择父节点所有儿子中子树最大的儿子,因此每次跳跃都能保证节点向上移动且不会遗漏LCA所在的路径。当两个节点跳到同一条重链时,说明它们之间的路径已经收敛到同一条链上,此时深度较小的节点必然是两者的最近公共祖先。整个过程不会跳过LCA,也不会遗漏任何可能的祖先节点,因此算法是正确的。
树链剖分求解树上修改查询问题
首先,让我们了解时间戳的概念。
在树链剖分中,时间戳通常指的是通过深度优先遍历DFS为每个节点分配的进入编号,即每个节点被遍历到的顺序编号。这样可以将树上的节点映射到一维数组上,便于使用线段树等数据结构进行区间操作。
具体来说,遍历树时为每个节点分配一个唯一的时间戳(如 \(dfn[u]\)),并记录每个子树的起止时间区间。这样,某个节点 \(u\) 的子树对应的区间就是 \([dfn[u], dfn[u] + size[u] - 1]\)。通过这个映射,可以高效地对树上路径或子树进行修改和查询操作。
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5;
vector<int>G[N];
int siz[N],deep[N],f[N],son[N],top[N],n,m,s,a[N],at[N],id[N],cnt,r,mod,root;
void dfs1(int u,int fa){
siz[u]=1;
f[u]=fa;
deep[u]=deep[fa]+1;
for(auto v:G[u]){
if(v!=fa){
dfs1(v,u);
siz[u]+=siz[v];
if(!son[u]||siz[son[u]]<siz[v]){
son[u]=v;
}
}
}
}
void dfs2(int u,int topu){
id[u]=++cnt;
at[cnt]=a[u];
top[u]=topu;
if(!son[u]){
return;
}
dfs2(son[u],topu);
for(auto v:G[u]){
if(v!=f[u]&&v!=son[u]){
dfs2(v,v);
}
}
}
struct node{
int l,r,num,laz;
}t[N];
int tot;
void addtag(int p,int l,int r,int val){
t[p].num+=((r-l+1)*val)%mod;
t[p].laz+=val;
}
void pushdown(int p,int l,int r){
if(t[p].laz!=0){
int mid=l+r>>1;
addtag(t[p].l,l,mid,t[p].laz);
addtag(t[p].r,mid+1,r,t[p].laz);
t[p].laz=0;
}
}
void build(int &p,int l,int r){
p=++tot;
if(l==r){
t[p].num=at[l];
return;
}
int mid=l+r>>1;
build(t[p].l,l,mid);
build(t[p].r,mid+1,r);
t[p].num=(t[t[p].l].num+t[t[p].r].num)%mod;
}
void modtif(int p,int ql,int qr,int l,int r,int val){
if(ql>r||qr<l){
return;
}
if(ql<=l&&r<=qr){
addtag(p,l,r,val);
return;
}
pushdown(p,l,r);
int mid=l+r>>1;
modtif(t[p].l,ql,qr,l,mid,val);
modtif(t[p].r,ql,qr,mid+1,r,val);
t[p].num=(t[t[p].l].num+t[t[p].r].num)%mod;
}
int query(int p,int ql,int qr,int l,int r){
if(ql>r||qr<l){
return 0;
}
if(ql<=l&&r<=qr){
return t[p].num;
}
pushdown(p,l,r);
int mid=l+r>>1;
return (query(t[p].l,ql,qr,l,mid)+query(t[p].r,ql,qr,mid+1,r))%mod;
}
void uprange(int x,int y,int val){
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]){
swap(x,y);
}
modtif(root,id[top[x]],id[x],1,n,val);
x=f[top[x]];
}
if(deep[x]<deep[y]){
swap(x,y);
}
modtif(root,id[y],id[x],1,n,val);
}
int qrange(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]]){
swap(x,y);
}
ans=(query(root,id[top[x]],id[x],1,n)+ans)%mod;
x=f[top[x]];
}
if(deep[x]<deep[y]){
swap(x,y);
}
ans=(ans+query(root,id[y],id[x],1,n))%mod;
return ans;
}
int main(){
cin>>n>>m>>r>>mod;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(r,0);
dfs2(r,r);
build(root,1,n);
for(int i=1;i<=m;i++){
int op,x,y,z;
cin>>op;
if(op==1){
cin>>x>>y>>z;
uprange(x,y,z);
}
else if(op==2){
cin>>x>>y;
cout<<qrange(x,y)%mod<<"\n";
}
else if(op==3){
cin>>x>>z;
modtif(root,id[x],id[x]+siz[x]-1,1,n,z);
}
else{
cin>>x;
cout<<query(root,id[x],id[x]+siz[x]-1,1,n)%mod<<"\n";
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号