CF1016D Vasya And The Matrix Solution

题目传送门

做法

因为是异或运算，可以按位考虑。

先预处理出行 ( $a[i]$ ) 异或和 $suma$，与列 ( $b[i]$ ) 的异或和 $sumb$。

• 如果 $suma \ne sumb$，那就说明无解，因为 $suma$ 和 $sumb$ 最后都代表着整个矩阵的异或和，如果两者不相等，那就说明矛盾，无解。

• 否则就一定存在解。

具体地，设 $ans[n][m]$ 为最终的答案矩阵，对于 $n-1,m-1$ 的子矩阵我们可以全部填上 $0$ ，其余的部分就为：

$ans[i][m]=a[i]~(i \in [1,n-1]),~ans[n][j]=b[j]~(j\in[1,m-1])$。

$ans[n][m]=(suma ~~ \text{xor} ~~ a[n]) ~~ \text{xor} ~~ b[m]$。

前面这两行的意思都是为满足题意，第一行就是直接填上原来的数（因为它前面的数都是一堆 $0$ ，也就是这一行或者这一列只受一个因素影响，所以直接填上原数不会对答案造成影响），第二行因为 $ans[n][m]$ 同时被两个因素 $a[n]$ 与 $b[m]$ 影响，所以要单独讨论。

$suma ~~ \text{xor} ~~ a[n]$ 的结果是整个矩阵前 $n-1$ 行的异或和，用它在 $\text{xor} ~~ b[m]$ 的结果是长这个样子：

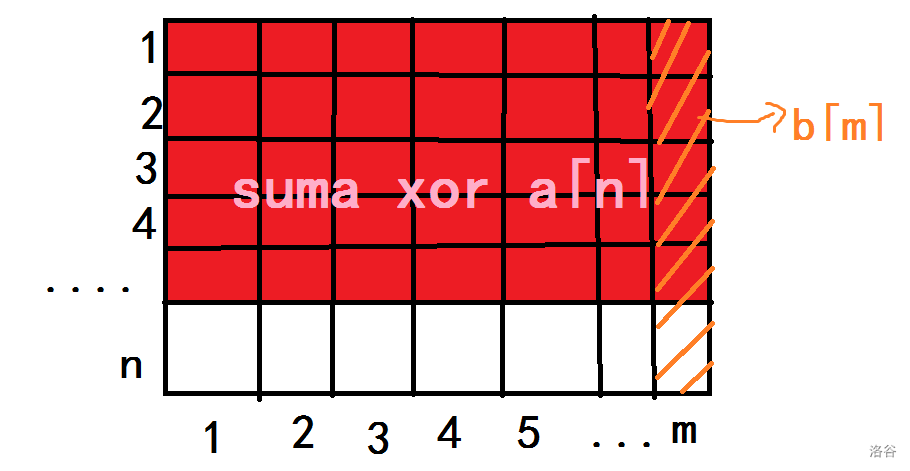
又因为 $ans[1,~...~,n-1][1,~...~,m-1]$ 都为 $0$ ，所以 $suma ~ \text{xor}~ a[n]$ 就是 $ans[1][m],ans[2][m],...ans[n-1][m]$ 的异或和。用这个结果在异或 $b[n]$ 就刚好是 $ans[n][m]$ 。

现在来考虑此做法的正确性，显然在判断无解的情况我们是没有问题的，有解时的对答案矩阵的构造方案也显然是对的。所以正确性得到了证明。

$Code$

#include<bits/stdc++.h>
using namespace std;
const int N=200;
int n,m,a[N],b[N],ans[N][N];
int main()
{
    int suma=0,sumb=0;
    scanf("%d %d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]),suma^=a[i];
    for(int i=1;i<=m;i++)scanf("%d",&b[i]),sumb^=b[i];
    if(suma!=sumb)
    {
        printf("NO\n");
        return 0;
    }
    printf("YES\n");
    for(int i=1;i<=n-1;i++)
        for(int j=1;j<=m-1;j++)ans[i][j]=0;
    for(int i=1;i<=n-1;i++)ans[i][m]=a[i];
    for(int i=1;i<=m-1;i++)ans[n][i]=b[i];
    ans[n][m]=b[m]^(suma^a[n]);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
            printf("%d ",ans[i][j]);
        printf("\n");
    }
    return 0;
}