《算法学习专栏》—— DP问题之状态压缩模型

2023年10月17日

更新于10月17日

一、前言

本栏，为状态压缩模型，题目主要来源日常，目前主要来源于Acwing的提高课。希望以后做到状态压缩的题目，也能加进来，不断完善。使用的分析方法均为闫式DP分析法。字臭。。。希望能用手写板慢慢写的好看。

二、状态压缩模型

2.1 解决的类型

1. 棋盘式状态压缩

2.2 一般的状态压缩步骤

1. 找到所有的合法状态
2. 分析能够转移的状态
3. 保存可以相互转移的状态
4. 遍历每一行
5. 遍历每一个合法的起始状态
6. 遍历每一个合法的转移状态

三、例题实战

1. Acwing1064 小国王

题目理解

代码实现

const int N = 12, M = (1 << N) + 10, K = 110;
int n, m;
ll f[N][K][M];
vector<ll> state;	// 每一个合法状态
ll id[M], cnt[M];		// 每一个状态和下标直接的映射关系， cnt是每一个状态中1的个数
vector<ll> head[M];		// 每一个状态可以转移到的其他状态


bool check(int u)
{
	for(int i = 0; i < n; i++)
		if((u >> i & 1) && (u >> (i + 1) & 1))
			return false;

	return true;
}

int count(int u)
{
	int res = 0;
	for(int i = 0; i < n; i++)
		if(u >> i & 1)res++;

	return res;
}

void solve()
{
	cin >> n >> m;

	
	// 找到合法状态
	for(int i = 0; i < 1 << n; i++)
		if(check(i))		// 是否存在两个连续的1
			state.push_back(i);	

	// 处理哪两个状态可以相互转移
	for(int i = 0; i < (int)state.size(); i++)
		for(int j = 0; j < (int)state.size(); j++)
		{
			int a = state[i], b = state[j];
			if((a & b) == 0 && check(a | b))	// 条件
				head[a].push_back(b);
		}


	f[0][0][0] = 1;
	for(int i = 1; i <= n + 1; i++)	// 多算一行hh，可以把答案好写
		for(int j = 0; j <= m; j++)
			for(int a = 0; a < (int)state.size(); a++)
				for(int b = 0; b < (int)head[state[a]].size(); b++)
				{
					int c = count(state[a]);
					if(j >= c)	// 一定要满足摆放的上限
						f[i][j][state[a]] += f[i - 1][j - c][head[state[a]][b]];

				}

	
	cout << f[n + 1][m][0];		// 拜访了n + 1行，但是摆了0个
	return;
}

2. Acwing327 玉米田

题目理解

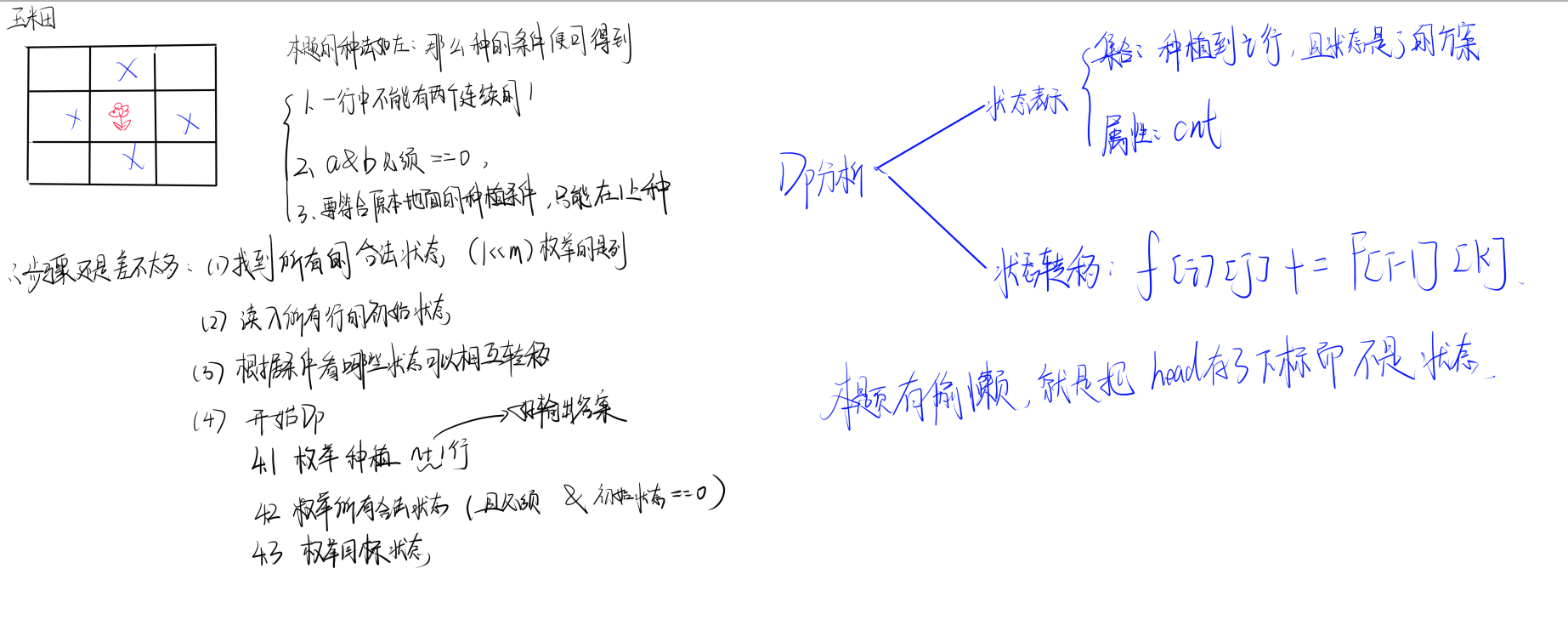
代码实现

const int N = 15, M = (1 << 12) + 10;

int n, m;
int w[N], f[N][M];
vector<int> state;
vector<int> head[M];


bool check(int u)
{
	for(int i = 0; i < m - 1; i++)
		if(u >> i & 1 && (u >> (i + 1)) & 1)
			return false;

	return true;
}


void solve()
{
	cin >> n >> m;

	for(int i = 1; i <= n; i++)
		for(int j = 0; j < m; j++)
		{
			int t;
			cin >> t;
			w[i] += !t * (1 << j);	// 第i行的情况
		}

	for(int i = 0; i < (1 << m); i++)
		if(check(i))
			state.push_back(i);


	for(int i = 0; i < (int)state.size(); i++)
		for(int j = 0; j < (int)state.size(); j++)
		{
			int a = state[i], b = state[j];	// 开始状态和目标状态
			if(!(a & b))	// 上面种了下面不能中，所以不能让a & b == 1
				head[i].push_back(j);
		}


	f[0][0] = 1;
	for(int i = 1; i <= n + 1; i++)
		for(int j = 0; j < (int)state.size(); j++)
			if(!(state[j] & w[i]))
				for(int k = 0; k < (int)head[j].size(); k++)
					f[i][j] = (f[i][j] + f[i - 1][head[j][k]]) % Mod;

	cout << f[n + 1][0];
	return;
}

3. Acwing292 炮兵阵地

题目理解

代码实现

const int N = 110, M = 10, S = (1 << M) + 10;

int n, m;
int g[N];
int f[2][S][S];
vector<int> state;
int cnt[S];

bool check(int u)
{
	for(int i = 0; i < m; i++)
		if(u >> i & 1 && (((u >> (i + 1)) & 1) || ((u >> (i + 2)) & 1)))
			return false;

	return true;
}

int count(int u)
{
	int res = 0;
    for (int i = 0; i < m; i ++ )
        if (u >> i & 1)
            res ++ ;
    return res;
}

void solve()
{
	cin >> n >> m;

	// 获取初始地图
	for(int i = 0; i < n; i++)
		for(int j = 0; j < m; j++)
		{
			char c;
			cin >> c;
			if(c == 'H') g[i] += 1 << j;
		}

	// 获取合法状态
	for(int i = 0; i < (1 << m); i++)
		if(check(i))
		{
			state.push_back(i);
			cnt[i] = count(i);
		}

	for(int i = 0; i < n + 2; i++)
		for(int j = 0; j < (int)state.size(); j++)
			for(int k = 0; k < (int)state.size(); k++)
				for(int u = 0; u < (int)state.size(); u++)
				{
					int a = state[u], b = state[j], c = state[k];
					if((a & b) || (a & c) || (b & c)) continue;	// 没有交集
					if(g[i] & c) continue;	// 不放山上

					f[i & 1][j][k] = max(f[i & 1][j][k], f[(i - 1) & 1][u][j] + cnt[c]);
				}

	cout << f[(n + 1) & 1][0][0];

	return;
}

4. Acwing291 蒙德里安的梦想

题目理解

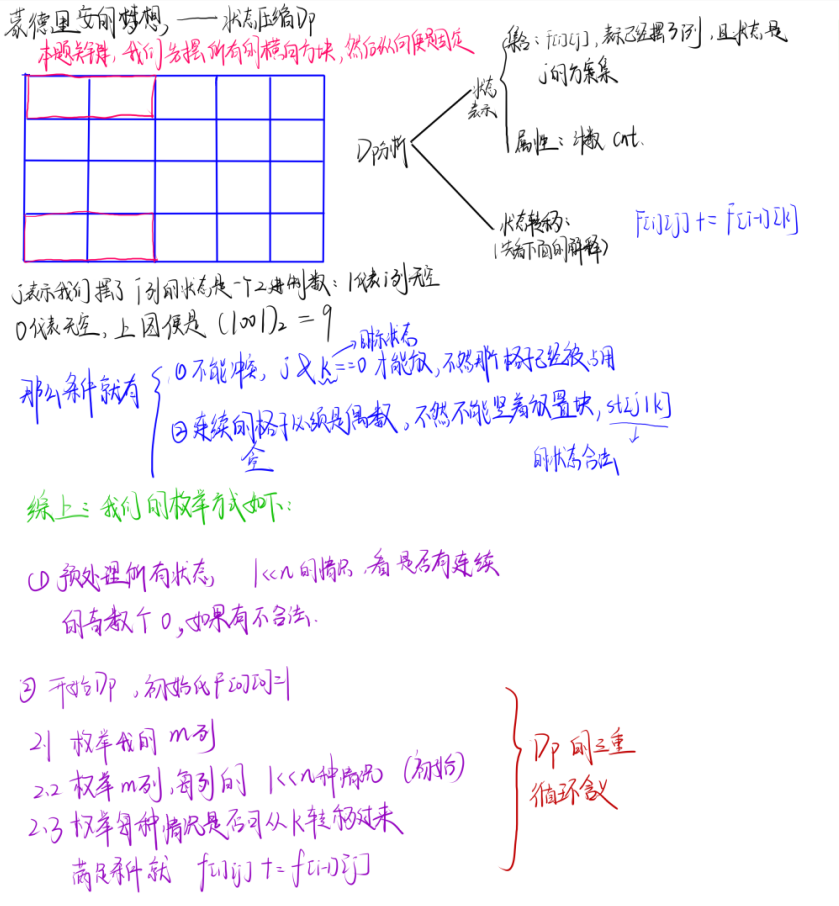
代码实现

const int N = 12, M = 1 << N;

int n, m;
ll f[N][M];
bool st[M];


void solve()
{
	while(cin >> n >> m, n || m)
	{
		memset(f, 0, sizeof f);
		memset(st, 0, sizeof st);

		// 预处理所有的状态，是否不存在连续奇数个0
		for(int i = 0; i < 1 << n; i++)
		{
			st[i] = true;
			int cnt = 0;

			for(int j = 0; j < n; j++)
				if(i >> j & 1) // 当前这一位是1
				{
					if(cnt & 1) st[i] = false;	//cnt & 1 == cnt % 2
					cnt = 0;
				}else cnt++;

			if(cnt & 1) st[i] = false;  // 查看连续的空着的个数是否为奇数
		}

		// 开始dp
		f[0][0] = 1; 	// 最开始的时候
		for(int i = 1; i <= m; i++)
			for(int j = 0; j < 1 << n; j++)
				for(int k = 0; k < 1 << n; k++)
					if((j & k) == 0 && st[j | k])
						f[i][j] += f[i - 1][k];

		cout << f[m][0] << endl;
	}


	return;
}