《算法学习专栏》—— DP问题之背包模型

2023年10月11日

更新于2023年10月15日习题更新至19

一、前言

本栏，为背包模型，题目主要来源日常，目前主要来源于Acwing的提高课。希望以后做到背包的题目，也能加进来，不断完善。使用的分析方法均为闫式DP分析法。字臭。。。希望能用手写板慢慢写的好看。

二、背包模型

2.1 目前的模型

01背包模型
完全背包模型
多重背包模型
分组背包模型
多维费用背包模型
有依赖的背包模型

2.2 解决的问题

背包模型的最多不超过类型问题（\(f 全为 0\)且\(v >= 0\)）
背包模型的恰好类型问题（\(f[0] == 0\)且\(v >= 0\)）
背包模型的至少类型问题（\(f[0] == 0\)且\(v无限制，可以取小于零\)，方案和max(0, j - v)即可）
背包模型的方案数问题（不是最优）
背包模型的具体方案问题（分组背包）
多维背包模型的上述三类问题
背包模型求最优方案数
背包模型求最优具体方案
...待更新、总结

2.3 降维优化

所有的背包模型都可以进行降维优化但要切记：

完全背包模型，正向枚举
其他背包，逆向枚举

三、题目实例

1. Acwing2 01背包问题

题目理解

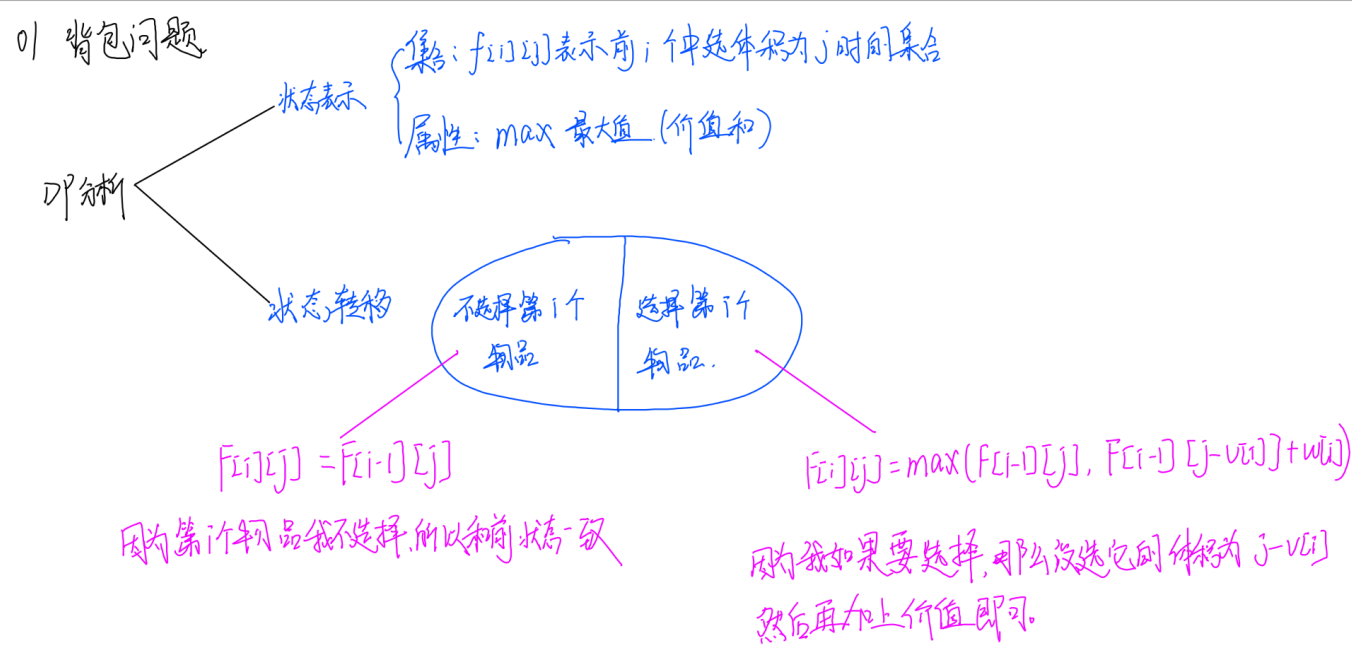
代码实现


const int N = 1010;
int f[N][N];
int w[N], v[N];
int n, m;
int main()
{
    
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; i++)
        for(int j = 0; j <= m; j++)
        {
            
            if(j >= v[i])
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
            else
                f[i][j] = f[i - 1][j];       
        }
    
    cout << f[n][m];
    
    return 0;
}

2. Acwing3 完全背包问题

题目理解

代码实现

const int N = 1010;
int f[N][N];
int n, m;
int w[N], v[N];

int main()
{
    cin >> n >>m;
    for(int i = 1; i <= n ;i++)
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++)
        for(int j =1; j <= m; j++)
            {
                f[i][j] = f[i - 1][j];
                if(j >= v[i])
                    f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
            }


    cout<<f[n][m];
    return 0;
}

3. Acwing4 多重背包问题

题目理解

代码实现

const int N = 1010;
int n, m;
int f[N][N];
int w[N], v[N], s[N];


int main()
{
   cin >> n >>m;
   for(int i = 1; i <= n ;i++)
       cin >> v[i] >> w[i] >> s[i];

    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            for(int k = 0 ; k <= s[i] && k * v[i] <= j; k++)
                f[i][j] = max(f[i][j], f[i-1][j - k*v[i]] + k * w[i]);

    cout<<f[n][m];
    return 0;
}

4. Acwing9 分组背包问题

题目理解

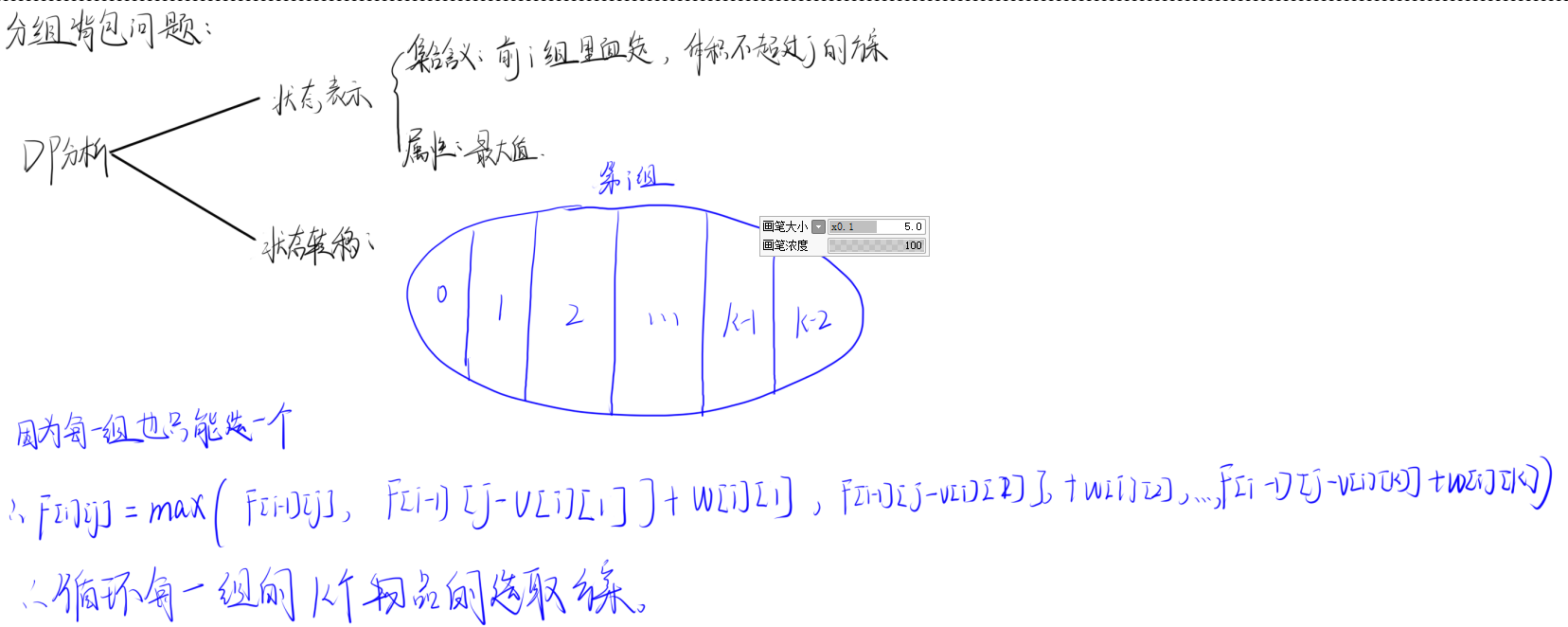
代码实现

const int N = 110;
int f[N][N], w[N][N], v[N][N];
int n, m, s[N];
int main()
{
    cin >> n >>m;
    for(int i = 1; i <= n; i++)
    {
        cin >> s[i];
        for(int j = 1; j <= s[i]; j++)
            cin >> v[i][j] >> w[i][j];

    }

    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        {
            f[i][j] = f[i-1][j];
            for(int k = 0; k <= s[i]; k++)
            {

                if(v[i][k] <= j)
                    f[i][j] = max(f[i][j], f[i-1][j-v[i][k]] + w[i][k]);
            }
        }


    cout<<f[n][m];
    return 0;
}

5. Acwing423 采药 01背包问题不超过类型

题目理解

代码实现

const int N = 1010;
int d[N][N], w[N], t[N];

void solve()
{
	int m, n;
	cin >> m >> n;

	for(int i = 1; i <= n; i++) cin >> t[i] >> w[i];

	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
		{
			d[i][j] = d[i - 1][j];
			if(j >= t[i])
				d[i][j] = max(d[i][j], d[i - 1][j - t[i]] + w[i]);
		}

	cout << d[n][m];

	return;
}

6. Acwing1024 装箱问题 01背包问题不超过类型

题目理解

代码实现

const int N = 40, M = 20000 + 10;
int w[N], d[N][M];

void solve()
{
	int n, v;
	cin >> v >> n;

	for(int i = 1; i <= n; i++) cin >> w[i];

	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= v; j++)
		{
			d[i][j] = d[i - 1][j];
			if(j >= w[i])
				d[i][j] = max(d[i - 1][j], d[i - 1][j - w[i]] + w[i]);
		}

	cout << v - d[n][v];
	return;
}

7. Acwing1022 多费用01背包问题不超过类型

题目理解

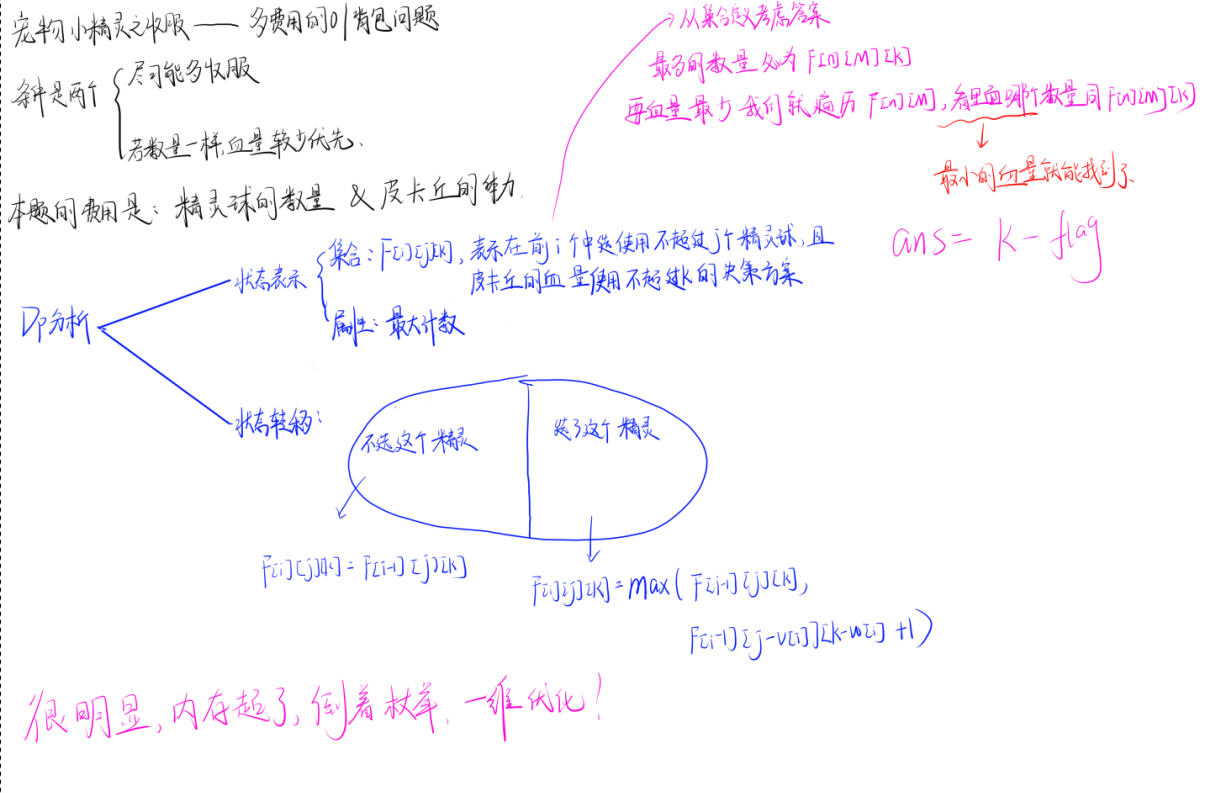
代码实现

const int M = 1010, N = 110, K = 510;
int f[M][K];
int v[N], w[N];


void solve()
{
	int n, m, k;
	cin >> m >> k >> n;

	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

	for(int i = 1; i <= n; i++)
		for(int j = m; j >= v[i]; j--)
			for(int p = k; p >= w[i]; p--)
					f[j][p] = max(f[j][p], f[j - v[i]][p - w[i]] + 1);

	int res = f[m][k - 1];
	int blood = 0;
	for(int i = 0; i <= k; i++)
		if(f[m][i] == res)
		{
			blood = i;
			break;
		}

	cout << res << " " << k - blood;
	return;
}

8. Acwing278 数字组合 01背包问题恰好类型方案数问题

题目理解

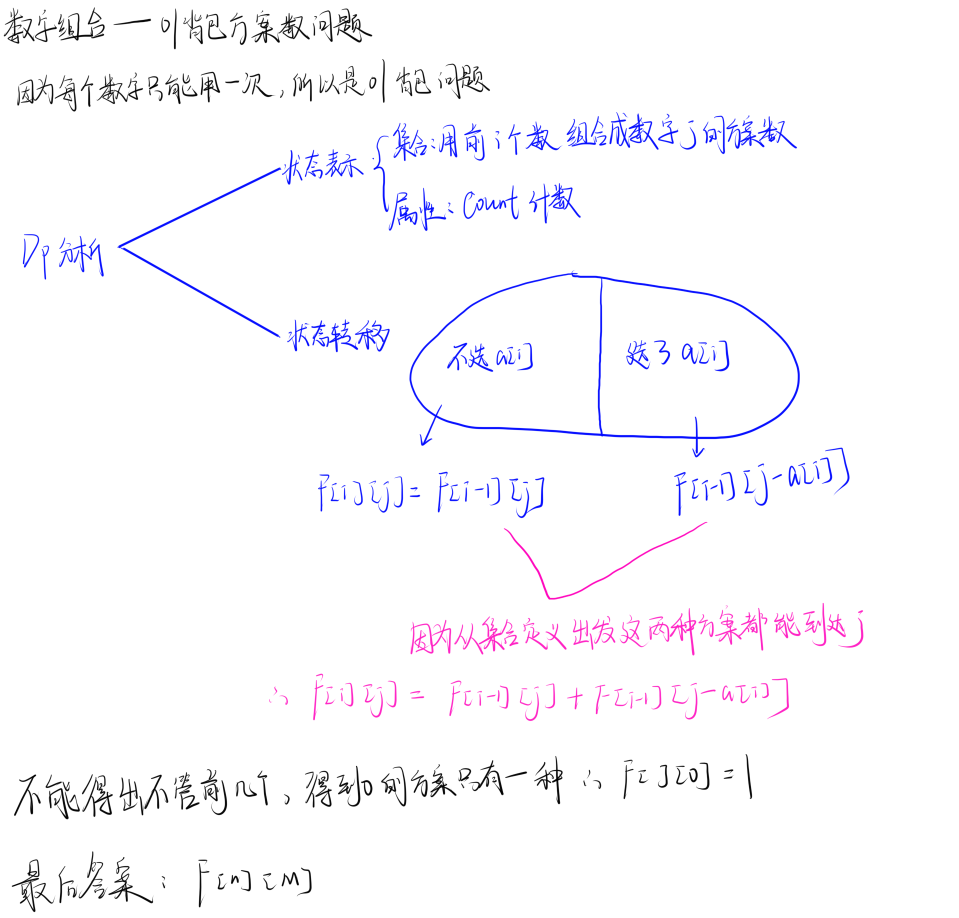
代码实现

const int N = 110, M = 100010;
int f[M], a[N];
void solve()
{
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> a[i];

	f[0] = 1;

	for(int i = 1; i <= n; i++)
		for(int j = m; j >= a[i]; j--)
			f[j] += f[j - a[i]];


	cout << f[m];
	return;
}

9. Acwing1023 买书完全背包问题方案数不超过类型

题目理解

代码实现

const int N = 1010;
int a[5] = {0, 10, 20, 50, 100}, f[N];
void solve()
{

	int n;
	cin >> n;

	f[0] = 1;

	for(int i = 1; i <= 4; i++)
		for(int j = a[i]; j <= n; j++)
				f[j] += f[j - a[i]];

	cout << f[n];
	return;
}

10. Acwing1021 货币系统完全背包问题方案数不超过类型

题目理解

代码实现

const int N = 20, M = 3010;
ll a[N], f[N][M], n, m;
void solve()
{

	cin >> n >> m;

	for(int i = 1; i <= n; i++) cin >> a[i];

	for(int i = 0; i <= n; i++) f[i][0] = 1;

	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
		{
			f[i][j] = f[i - 1][j];
			if(j >= a[i])
				f[i][j] += f[i][j - a[i]];
		}

	cout << f[n][m];
	return;
}

11. Acwing1019 庆功会多重背包问题不超过类型

题目理解

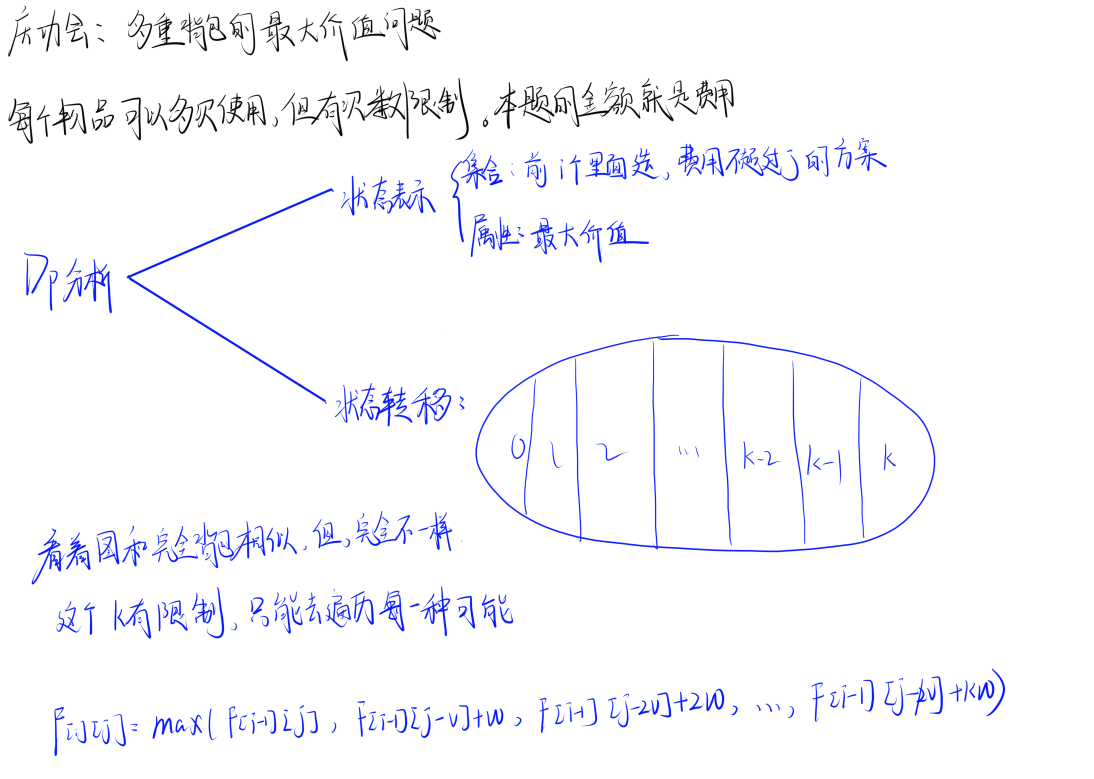
代码实现

const int N = 510, M = 6010;

int f[N][M], v[N], w[N], n, m, s[N];

void solve()
{

	cin >> n >> m;

	for(int i = 1; i <= n; i++)
		cin >> v[i] >> w[i] >> s[i];

	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
		{
			f[i][j] = f[i - 1][j];

			for(int k = 0; k <= s[i]; k++)
				if(k * v[i] <= j)
					f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
		}


	cout << f[n][m];
	return;
}

12. Acwing1020 潜水员多费用01背包问题至少类型

题目理解

代码实现

const int N = 30, M = 90, K = 1010;
int f[K][N][M], s[K], v[K], w[K];

void solve()
{
	memset(f, INF, sizeof f);

	int n, m, k;
	cin >> m >> k >> n;

	for(int i = 1; i <= n; i++)
		cin >> s[i] >> v[i] >> w[i];

	for(int i = 0; i <= n; i++) f[i][0][0] = 0;

	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
			for(int p = 1; p <= k; p++)
			{
				f[i][j][p] = f[i - 1][j][p];
				f[i][j][p] = min(f[i][j][p], f[i - 1][max(0, j - s[i])][max(0, p - v[i])] + w[i]);
			}

			
	cout << f[n][m][k];

	return;
}

13. Acwing1013 机器分配分组背包问题不超过类型、具体方案问题

题目理解

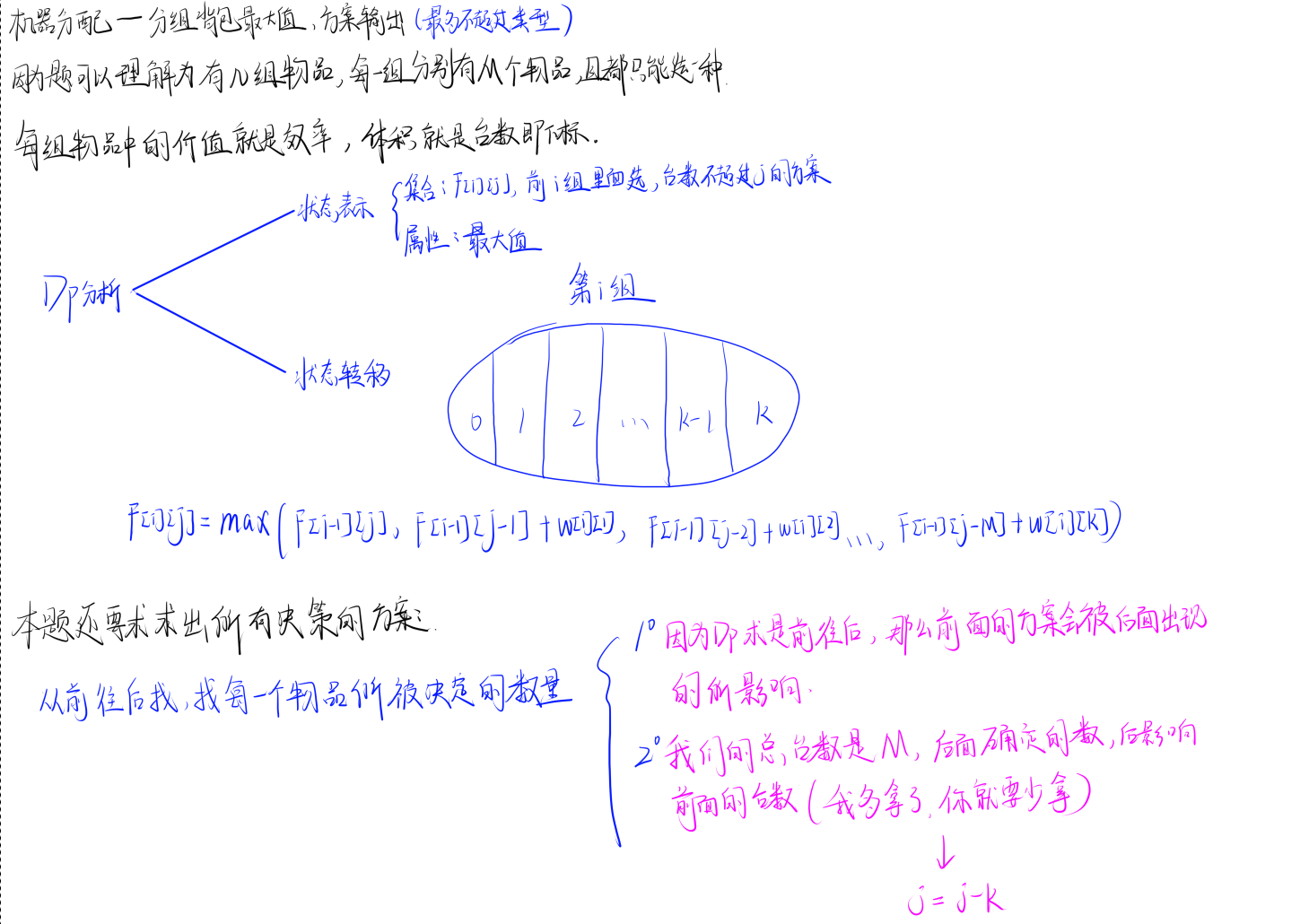
代码实现

const int N = 20, M = 20;
int w[N][N], f[N][M], p[N];
void solve()
{
	int n, m;
	cin >> n >> m;

	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
			cin >> w[i][j];

	for(int i = 1; i <= n; i++)
		for(int j = 0; j <= m; j++)
		{
			f[i][j] = f[i - 1][j];
			for(int k = 0; k <= j; k++)
					f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
		}

	cout << f[n][m] << endl;
	

	int j = m;

	for(int i = n; i; i--)
		for(int k = 0; k <= j; k++)
		{
			if(f[i][j] == f[i - 1][j - k] + w[i][k])
			{
				p[i] = k;
				j -= k;
				break;      // 不再往下找了
			}
		}


	for(int i = 1; i <= n; i++)
		cout << i << " " << p[i] << endl;

	return;
}

14. Acwing426 开心的金明 01背包问题不超过类型

题目理解

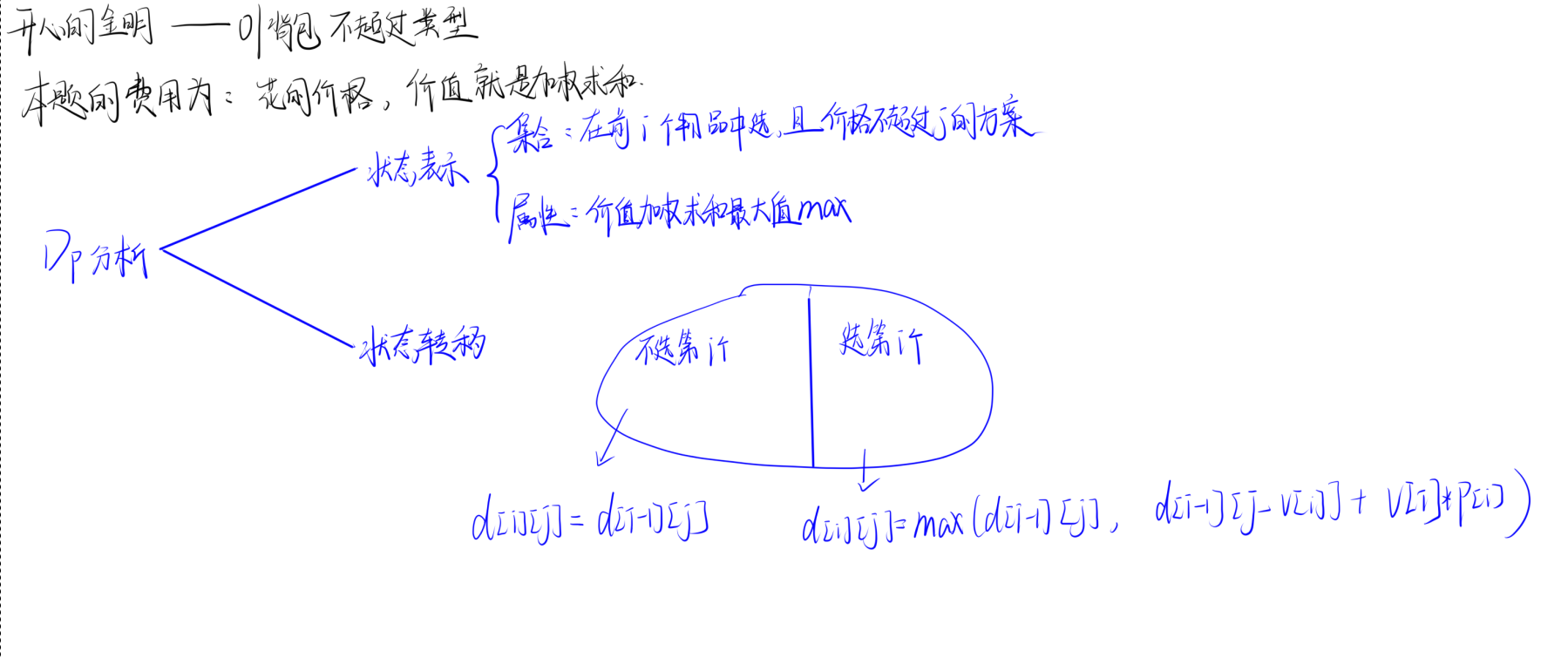
代码实现

const int N = 30000 + 10, M = 30;

ll d[N], p[M], v[M];
int n, m;
void solve()
{
	cin >> m >> n;

	for(int i = 1; i <= n; i++) cin >> v[i] >> p[i];

	for(int i = 1; i <= n; i++)
		for(int j = m; j >= v[i]; j--)
			d[j] = max(d[j], d[j - v[i]] + p[i] * v[i]);

	cout << d[m];

	return;
}

15. Acwing10 有依赖的背包问题

题目理解

代码实现

方案一

#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;

const int Mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int N = 110, M = N * 2;

int h[N], ne[M], e[M], idx, w[N], v[N], f[N][N]; 
int n, m;
void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u)
{
	// 分组背包循环物品组，也就是循环u的子节点
	for(int i = h[u]; ~i; i = ne[i])
	{
		int son = e[i];		// 取出子节点的编号
		dfs(e[i]);		// 继续递归处理子节点

		// 开始分组背包的循环
		// 首先是体积
		for(int j = m - v[u]; j >= 0; j--)	// 循环体积，这里是m - v[i]的
			for(int k = 0; k <= j; k++)		// 循环决策！因为我们的划分依据是体积，而不是选择物品
				f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
	}


	// 因为我们还没有把u的价值算进去, 所以要加上
	for(int i = m; i >= v[u]; i--) f[u][i] = f[u][i - v[u]] + w[u];
	for(int i = 0; i < v[u]; i++) f[u][i] = 0;

}

void solve()
{

	cin >> n >> m;
	int root;
	for(int i = 1; i <= n; i++)
	{
		int a;
		cin >> v[i] >> w[i] >> a;
		if(a == -1) root = i;	// 根节点的编号
		else add(a, i);
	}


	// 递归处理树形dp
	dfs(root);


	cout << f[root][m];		// 根节点必选，且体积不过m时的价值最大值
	return;
}

int main()
{
	memset(h, -1, sizeof h);
	int T = 1;
	while(T--) solve();
	return 0;
}

方案二

#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;

const int Mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int N = 110, M = N * 2;

int h[N], ne[M], e[M], idx, w[N], v[N], f[N][N]; 
int n, m;
void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u)
{
	for(int i = v[u]; i <= m; i++) f[u][i] = w[u];	// 因为必选所以把他们初始化为w[u]

	// 分组背包循环物品组，也就是循环u的子节点
	for(int i = h[u]; ~i; i = ne[i])
	{
		int son = e[i];		// 取出子节点的编号
		dfs(e[i]);		// 继续递归处理子节点

		// 开始分组背包的循环
		// 首先是体积
		for(int j = m; j >= v[u]; j--)	// 循环体积，体积绝不能小于v[u]
			for(int k = 0; k <= j - v[u]; k++)		// 循环决策！因为我们的划分依据是体积，而不是选择物品
				f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
	}
}

void solve()
{

	cin >> n >> m;
	int root;
	for(int i = 1; i <= n; i++)
	{
		int a;
		cin >> v[i] >> w[i] >> a;
		if(a == -1) root = i;	// 根节点的编号
		else add(a, i);
	}


	// 递归处理树形dp
	dfs(root);


	cout << f[root][m];		// 根节点必选，且体积不过m时的价值最大值
	return;
}

int main()
{
	memset(h, -1, sizeof h);
	int T = 1;
	while(T--) solve();
	return 0;
}

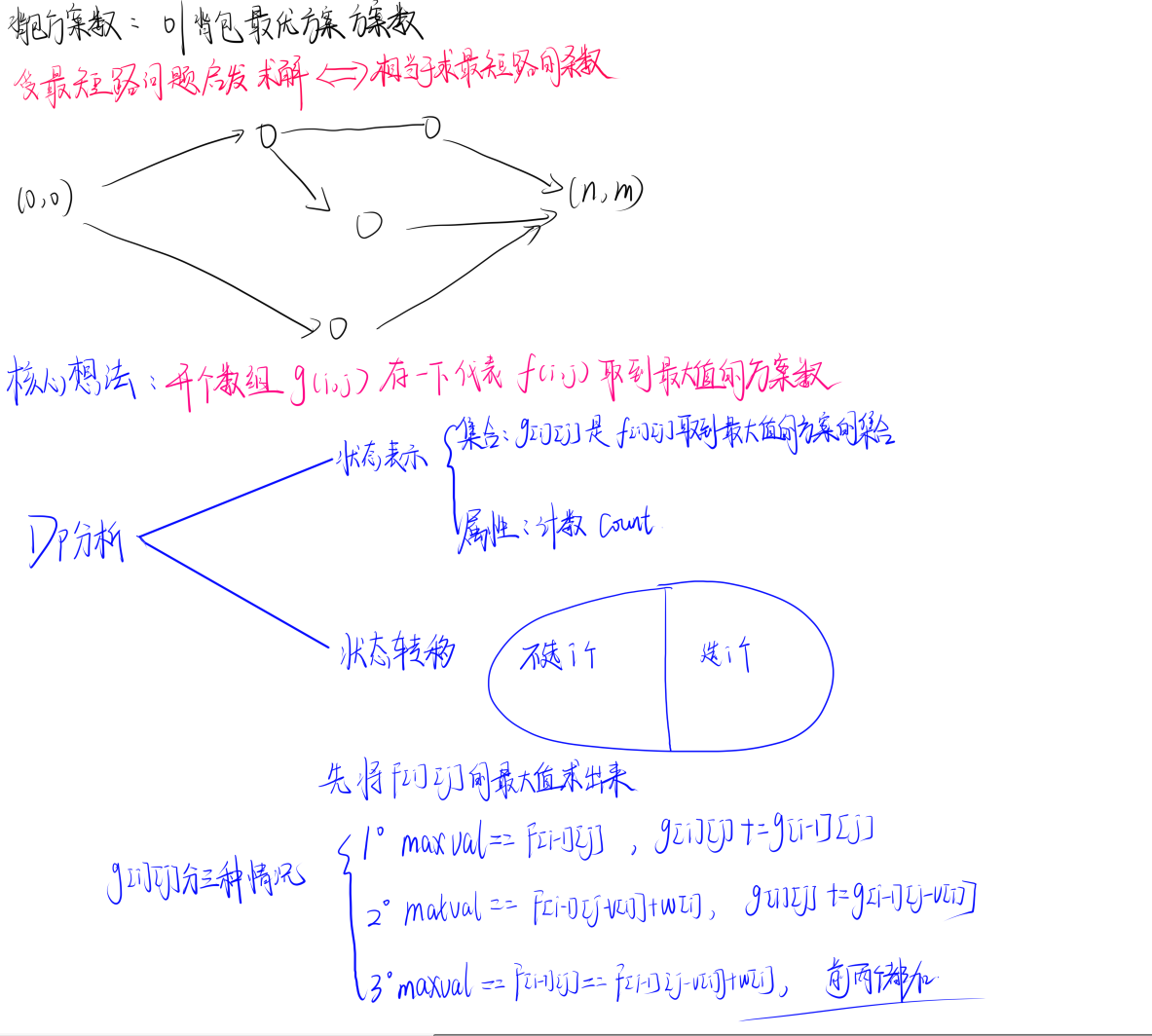
16. Acwing11 背包问题求方案数（最优）

题目理解

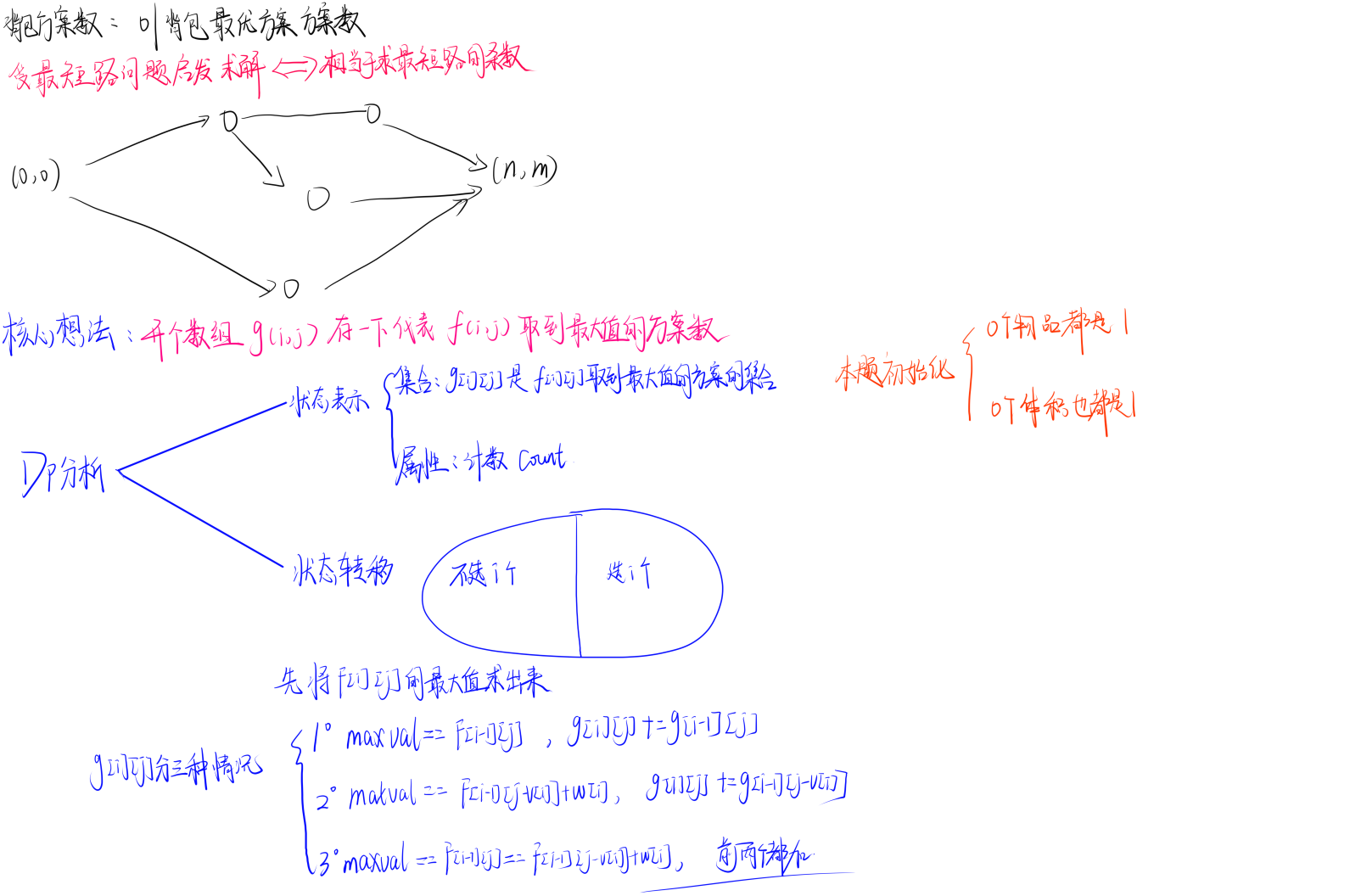
代码实现

#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;

const int Mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int N = 1010;
int g[N][N], f[N][N], v[N], w[N];
int n, m;

void solve()
{
	cin >> n >> m;

	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
	for(int i = 0; i <= n; i++) g[i][0] = 1;

	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
		{
			f[i][j] = f[i - 1][j];
			g[i][j] += g[i - 1][j];
			g[i][j] %= Mod;
			if(j >= v[i])
			{
				f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
				if(f[i][j] == f[i - 1][j - v[i]] + w[i]){ 
					g[i][j] += g[i - 1][j - v[i]];
					g[i][j] %= Mod;
				}
			}
		}

	cout << g[n][m];
	return;
}

int main()
{
	int T = 1;
	while(T--) solve();
	return 0;
}

17. Acwing12 背包问题求具体方案（最优方案）

题目理解

代码实现

#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;

const int Mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int N = 1010;

int g[N][N], v[N], w[N], d[N][N];
int n, m;
void solve()
{

	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];

	for(int i = n; i >= 1; i--)
		for(int j = 1; j <= m; j++)
		{
			d[i][j] = d[i + 1][j];
			if(j >= v[i])
				d[i][j] = max(d[i][j], d[i + 1][j - v[i]] + w[i]);
		}

	int j = m;
	for(int i = 1; i <= n; i++)
	{
		if(j >= v[i] && d[i][j] == d[i + 1][j - v[i]] + w[i])
		{
			cout << i << " ";
			j -= v[i];
		}
	}

	return;
}

int main()
{
	int T = 1;
	while(T--) solve();
	return 0;
}

18. Acwing487 金明的预算方案

题目理解

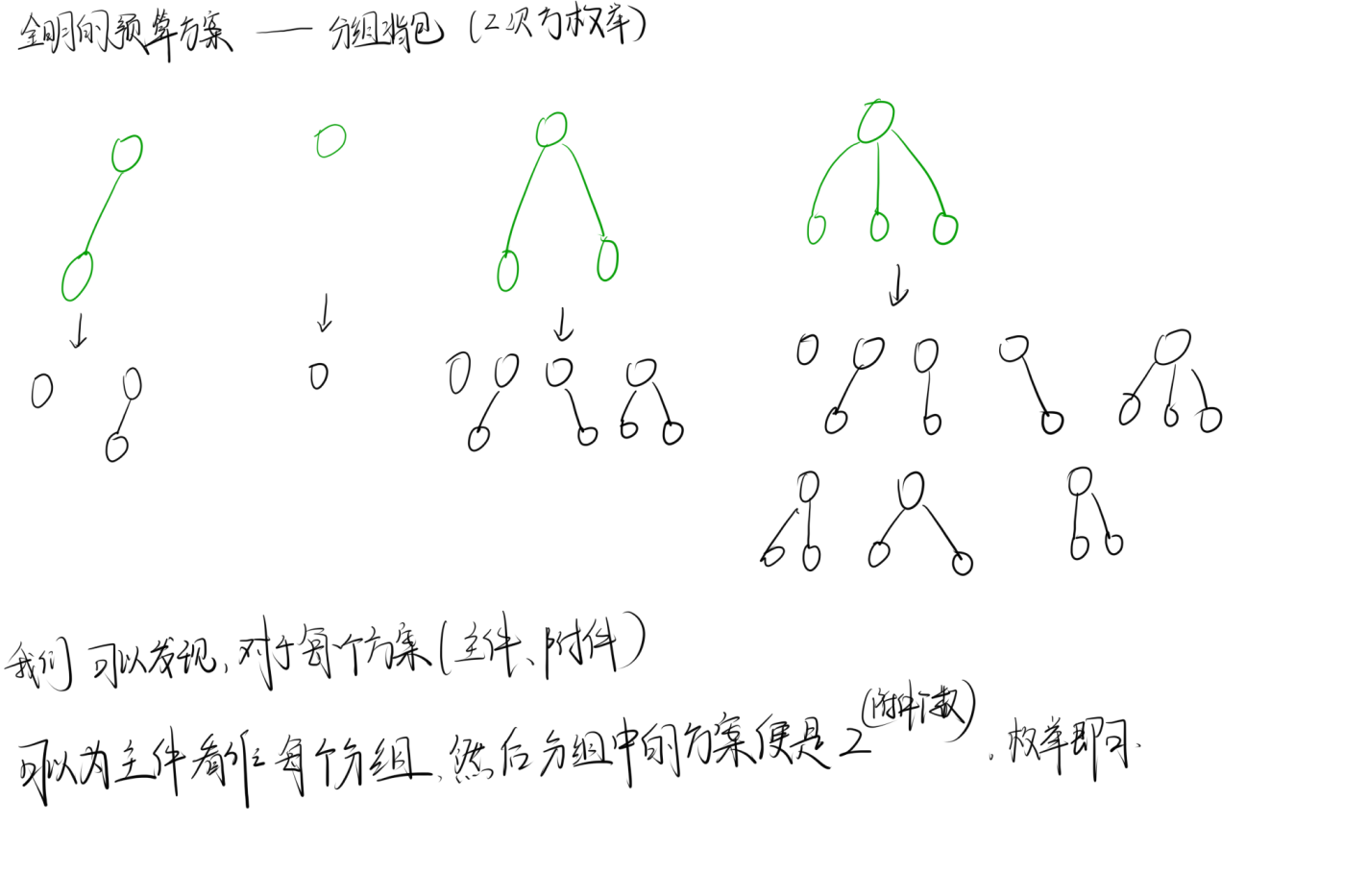
代码实现

const int N = 60, M = 32010;

int n, m;
PII master[N];
vector<PII> servent[N];
int f[M];

void solve()
{
	cin >> m >> n;

	for(int i = 1; i <= n; i++)
	{
		int v, p, q;
		cin >> v >> p >> q;
		p *= v;
		if(!q) master[i] = {v, p};
		else servent[q].push_back({v, p});
	}


	for(int i = 1; i <= n; i++)
		for(int u = m; u >= 0; u--)
		{
			for(int j = 0; j < 1 << servent[i].size(); j++)	// 二的n次种方案
			{
				int v = master[i].v, w = master[i].w;

				for(int k = 0; k < (int)servent[i].size(); k++)	// 枚举每一个从品
					if(j >> k & 1)
					{
						v += servent[i][k].v;
						w += servent[i][k].w;
					}
				if(u >= v) f[u] = max(f[u], f[u - v] + w);
			}
		}


	cout << f[m] << endl;
	return;
}

19. 蓝桥杯第一次双周赛 D 锻炼多个完全背包

题目理解

把可以连续锻炼的天数，当作我们的多个背包。然后对于每一段时间进行完全背包。可以用map即可相同的天数，进行优化。

代码实现

const int N = 2e5 + 10, M = (1 << 20) + 10;
ll f[M];
void solve()
{
	vector<ll> p;
	ll qq = 1;
	for(int i = 0; i < 22; i++)
	{
		p.push_back(qq);
		qq *= 2;
	}
	int n, m, q;
	cin >> n >> m >> q;
	ll res = 0;
	unordered_map<int, int> mp;
	int idx = 1;

	for(int i = 0; i < q; i++)
	{
		int x, day;
		cin >> x;

		day = x - idx;
			
		idx = x + 1;
		if(day <= 0 && i != q - 1) continue;
		if(!mp.count(day))
			mp[day] = 1;
		else mp[day]++;	

		if(i == q - 1)
		{
			if(!mp.count(n - x))
				mp[n-x] = 1;
			else 
				mp[n-x]++;
		}	
	}	

	vector<ll> v, w;

	for(int i = 0; i < m; i++)
	{
		ll a, b;
		cin >> a >> b;
		w.push_back(b);
		v.push_back(p[a]);
	}

	for(auto p : mp)
	{
		int V = p.x;
		memset(f, 0, sizeof f);
		for(int i = 0; i < m; i++)
			for(int j = v[i]; j <= V; j++)	// 完全背包正着枚举
			{
				f[j] = max(f[j], f[j - v[i]] + w[i]);
			}

		res += f[V] * p.y;
	}

	cout << res;
	return;
}

posted @ 2023-10-11 18:50 wxzcch 阅读(41) 评论(0) 收藏举报

刷新页面返回顶部

wxzcch

《算法学习专栏》—— DP问题之背包模型

更新于2023年10月15日 习题更新至19

一、前言

二、背包模型

2.1 目前的模型

2.2 解决的问题

2.3 降维优化

三、题目实例

1. Acwing2 01背包问题

题目理解

代码实现

2. Acwing3 完全背包问题

题目理解

代码实现

3. Acwing4 多重背包问题

题目理解

代码实现

4. Acwing9 分组背包问题

题目理解

代码实现

5. Acwing423 采药 01背包问题不超过类型

题目理解

代码实现

6. Acwing1024 装箱问题 01背包问题不超过类型

题目理解

代码实现

7. Acwing1022 多费用01背包问题不超过类型

题目理解

代码实现

8. Acwing278 数字组合 01背包问题恰好类型方案数问题

题目理解

代码实现

9. Acwing1023 买书 完全背包问题方案数不超过类型

题目理解

代码实现

10. Acwing1021 货币系统 完全背包问题方案数不超过类型

题目理解

代码实现

11. Acwing1019 庆功会 多重背包问题不超过类型

题目理解

代码实现

12. Acwing1020 潜水员 多费用01背包问题至少类型

题目理解

代码实现

13. Acwing1013 机器分配 分组背包问题不超过类型、具体方案问题

题目理解

代码实现

14. Acwing426 开心的金明 01背包问题不超过类型

题目理解

代码实现

15. Acwing10 有依赖的背包问题

题目理解

代码实现

16. Acwing11 背包问题求方案数（最优）

题目理解

代码实现

17. Acwing12 背包问题求具体方案（最优方案）

题目理解

代码实现

18. Acwing487 金明的预算方案

题目理解

代码实现

19. 蓝桥杯第一次双周赛 D 锻炼 多个完全背包

题目理解

代码实现

公告

更新于2023年10月15日习题更新至19

9. Acwing1023 买书完全背包问题方案数不超过类型

10. Acwing1021 货币系统完全背包问题方案数不超过类型

11. Acwing1019 庆功会多重背包问题不超过类型

12. Acwing1020 潜水员多费用01背包问题至少类型

13. Acwing1013 机器分配分组背包问题不超过类型、具体方案问题

19. 蓝桥杯第一次双周赛 D 锻炼多个完全背包