三分！船新的知识点！

题目链接

ACWING5201 午餐音乐会
这个题带我了解了三分！

题目描述

一维数轴上站着 N个人，编号 1∼N。初始时，第 i 个人位于整数坐标位置 Pi，此人移动 1单位距离所需的成本为 Wi,他能听到与他相距不超过Di的所有位置发出的声音。不同的人的位置可以重叠。现在，我们需要选择一个整数坐标位置，并在此位置举办一场音乐会。没有人想要错过这场音乐会，所以音乐会开始后，所有听不到音乐的人都会朝音乐会举办位置方向移动，直到移动至可以听到音乐的位置为止。我们希望合理选择音乐会的举办位置，使得所有人的移动总成本尽可能小。你输出这个总成本的最小可能值。

• 输入格式
  第一行包含一个整数N。
  接下来 N 行，每行包含三个整数 Pi,Wi,Di。

• 输出格式
  一个整数，表示最小总成本。

• 数据范围

\[1≤N≤2×10^{5} \]

\[0≤Pi≤10^{9} \]

\[1≤Wi≤1000 \]

\[0≤Di≤10^{9} \]

• 输入样例1：

1
0 1000 0

• 输出样例1：

0

• 样例1解释
  最佳方案是在位置 0 举办音乐会，这样唯一的人无需任何移动即可听到音乐会。

• 输入样例2：

2
10 4 3
20 4 2

• 输出样例2：

20

• 样例2解释
  一种最佳方案是在位置 14
  举办音乐会，这样的话，第一个人需要移动至位置 11
  ，所需成本为 (11−10)×4=4
  ，第二个人需要移动至位置 16
  ，所需成本为 (20−16)×4=16
  ，总成本为 4+16=20
  。

• 输入样例3：

3
6 8 3
1 4 1
14 5 2

• 输出样例3：

43

题目理解

对于我来说，这个题非常棒！是我完全没有做过的类型题。该题目需要完成一个目的就是让移动的消耗最少。
这个题的知识点是三分，因为我之前接触的二分，么办法解决，因为我没法确定是往左移损耗最小还是往右移动损耗最小。
我们经过分析题目可以得到如下图示结果：

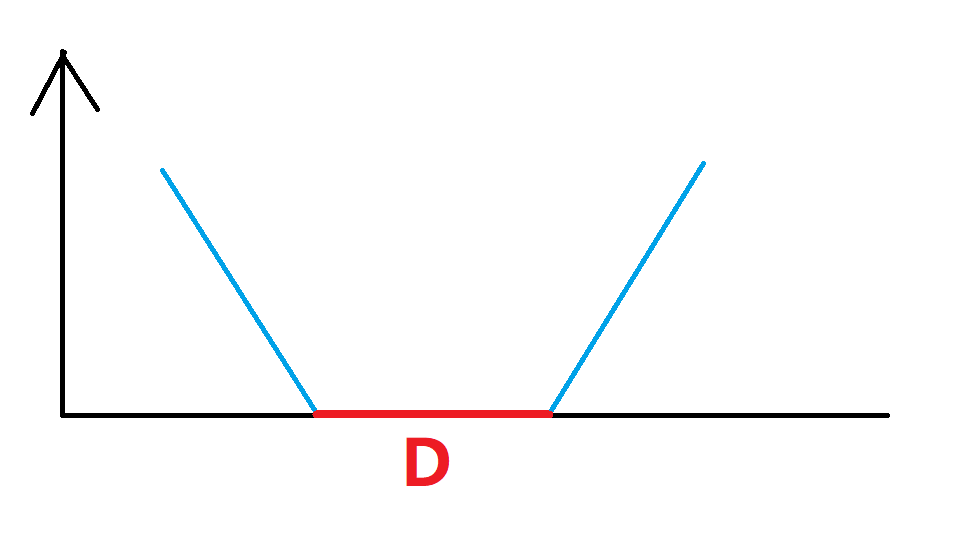
• 我们可以看出，只有在这个长度为D的区间，损耗是0，往两边都会增加。是一个下凸函数。
• 下凸函数有个性质，就是多个下凸函数求和，仍为下凸函数。
• 然后我们就可得到总的损耗变化趋势，如下图。
  
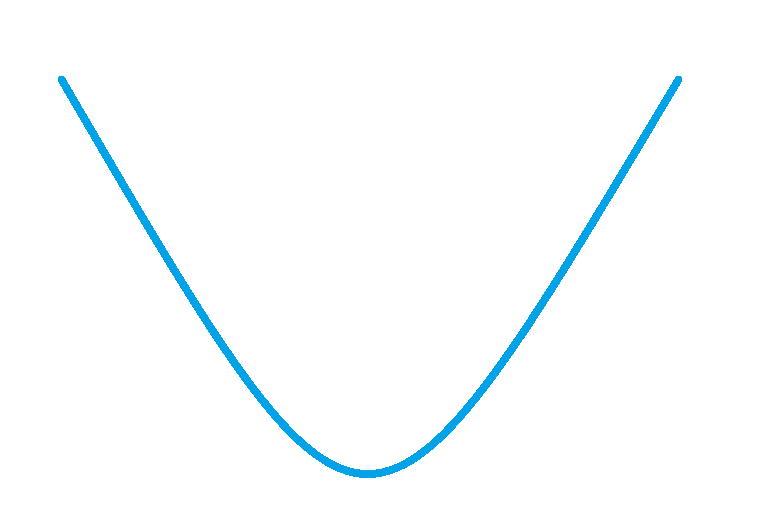
• 得到这个趋势，我们取三等分点。我们首先规定，左边的三等分点一定是大于等于右边的三等分点。那么就会有以下两种情况。
  
  
  很明显根据图示，橘色部分一定不会是答案，那么就可以把我的左边界，赋值为左三等分点！！
• 右三等分点的情况相同。可以将右三等分点右边的部分去掉！那么最后就可以找到答案啦！！
  这个题非常不错！学到了新东西！

代码实现

#include<iostream>
#include<cmath>
using namespace std;

const long long N = 2e5 + 10;

long long p[N], w[N], D[N];
int n;
int l = 0, r = 1e9;


long long check(long long u)
{

    long long sum = 0;


    for(long long i = 1; i <= n; i++)
    {
        if(abs(p[i] - u) > D[i])
        {

            if(u >= p[i])
                sum += w[i] * (u - p[i]  - D[i]);
            else
                sum += w[i] * (p[i] - u - D[i]);
        }
    }

    return sum;
}


int main()
{
    cin >> n;

    for(long long i = 1; i <= n; i++)
        cin >> p[i] >> w[i] >> D[i];


    while (l <= r)
    {
        int midl = l + (r - l) / 3;
        int midr = r - (r - l) / 3;
        if (check(midl) <= check(midr)) r = midr - 1;
        else l = midl + 1;
    }

    cout << min(check(l), check(r));

    return 0;
}