[2020多校联考]最大前缀和

Solution

答案只可能和前缀最大值相关，不妨枚举这个最大值 \(k\)。有 \(n\) 个 \(+1\)，所以范围是 \(1\) ~ \(n\)。答案就是

\[\sum_{k=1}^{n} k\times (最大前缀和为k的序列个数) \]

只需要求出后面那个。对于一个最大前缀和为 \(k\) 的序列，一定存在至少一个位置，使得该位置的前缀和等于 \(k\)。枚举第一个使条件成立的位置 \(2i+k\)，该位置上的数一定为 \(+1\)，该位置之前的前缀和一定不能达到 \(k\)。因为该位置的前缀和等于 \(k\)，所以该前缀一定恰由 \(k+i\) 个 \(+1\) 和 \(i\) 个 \(-1\) 组成。除去该位置的 \(+1\) ，选择该位置之前的数组成序列的方案就等价于从 \((0,0)\) 走到 \(((k+i-1)+(i),k-1)\)，有 \(k+i-1\) 次可以从 \((x,y)\) 走到 \((x+1,y+1)\)，有 \(i\) 次可以从 \((x,y)\) 走到 \((x+1,y-1)\)，且路径不经过 \(y=k\) 这条直线。如果不管经不经过这条直线，方案就有 \(\binom{(k+i-1)+(i)}{k+i-1}\) 种，再减去不合法的。

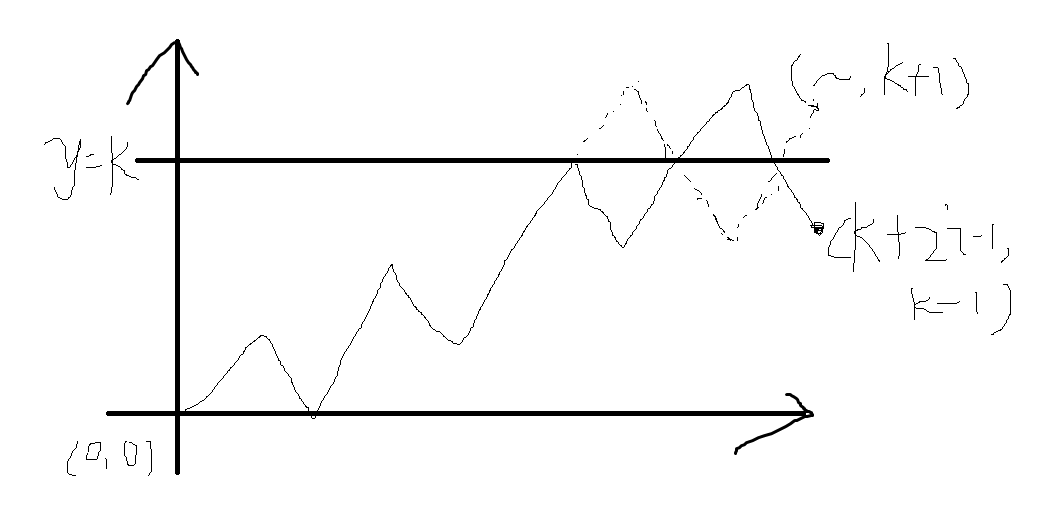
对于经过了这条直线的方案，将后面的翻上去，方案和从 \((0,0)\) 走到 \((k+2i-1,k+1)\) 一一对应，但注意此时向上走的机会多了 \(1\)，向下走的少了 \(1\)。那么就减去 \(\binom{k+2i-1}{i+1}\)。

对于第一个满足条件位置之后的位置，还剩下 \(n-i\) 个 \(+1\) 和 \(m+k-i\) 个 \(-1\)。组成的方案只要前缀不大于 \(0\) 即可（因为加上了前面的数），也就是不经过直线 \(y=1\)。类比上面，从 \((0,0)\) 走到 \((n+m-2i+k,n-m-k)\)，\(n-m-k\) 必须小于等于 \(0\)。若不考虑经不经过，方案为 \(\binom{n-2i+m+k}{n-i}\)。考虑不合法的。

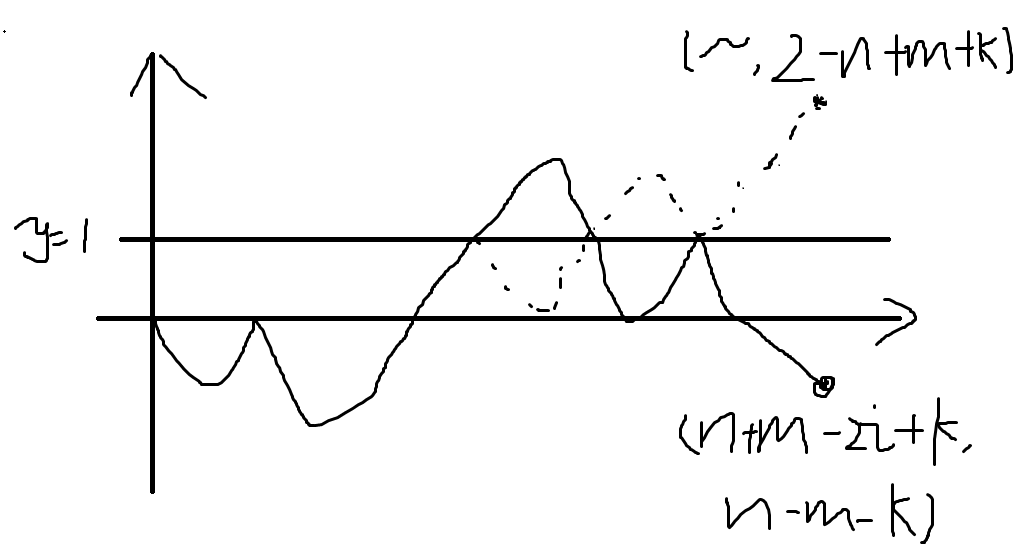
把后面翻过来，终点关于 \(y=1\) 对称，简单算一下可知，实质上是将 \(+1\) 和 \(-1\) 的个数交换，再加一个 \(+1\) 的个数，再减一个 \(-1\) 的个数。方案就为 \(\binom{n-2i+m+k}{m+k-i+1}\)

答案是 $$\sum_{k=1}^{n} k\times [\sum_{i=k}^{n} (\binom{k+2i-1}{k+i-1}-\binom{k+2i-1}{i+1})\times(\binom{n-2i+m+k}{n-i}-\binom{n-2i+m+k}{m+k-i+1})]$$

#include<stdio.h>
#define N 4007
#define Mod 998244853
#define ll long long

int n,m;
ll C[N][N];

ll mod(ll x){return (x%Mod+Mod)%Mod;}

int main(){
    freopen("maxpsum.in","r",stdin);
    freopen("maxpsum.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n+m;i++) C[i][0]=C[i][i]=1;
    for(int i=1;i<=n+m;i++)
        for(int j=1;j<i;j++)
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%Mod;
    ll ans=0;
    for(int k=1;k<=n;k++)
        for(int i=k;i<=n;i++){
            int x1=i-1,y1=i-k,x2=n-i,y2=m+k-i;
            if(y2<x2) continue;
            ans=mod(ans+k*mod(mod(C[x1+y1][x1]-C[x1+y1][x1+1])*mod(C[x2+y2][x2]-C[x2+y2][y2+1])));
        }
    printf("%lld",ans);
}