树链剖分笔记
定义申明
- 根节点的深度为 \(0\)。
- 一个节点的祖先和后代均包括自己。
- C++ 代码仅供参考,毕竟代码风格因人而异。
引入
首先要明确,树上任意两点均有公共祖先:根节点,所以 LCA 问题总是有解的。
直接跟着题意做,找出两个点的所有祖先,然后找它们的交集中与两点距离最近的点。
先举个例子,如下图,求 \(16\) 与 \(19\) 的 LCA。
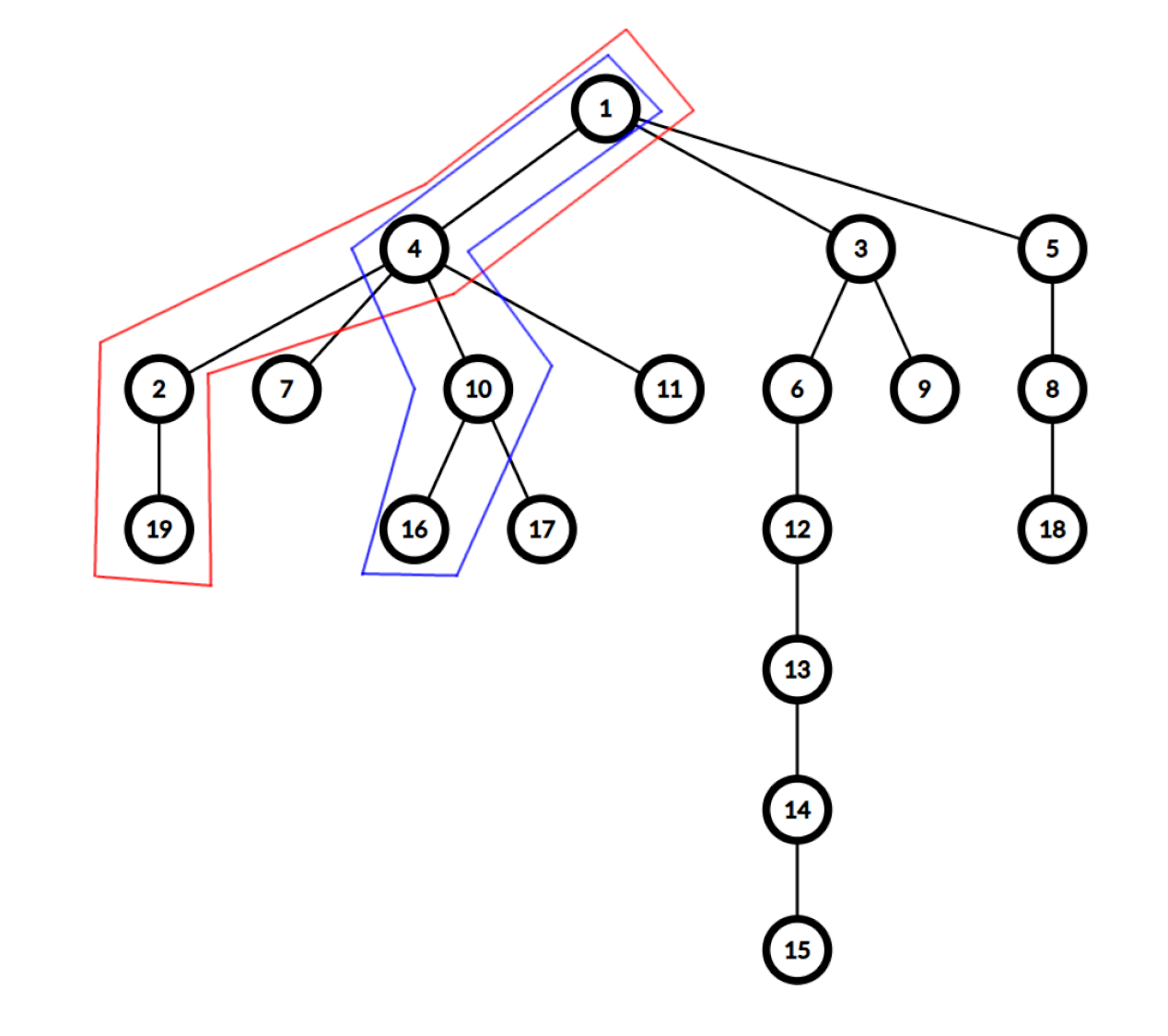
可知,\(16\) 的祖先集合为 \(\{16, 10, 4, 1\}\),\(19\) 的祖先集合为 \(\{19, 2, 4, 1\}\)。它们的交集是 \(\{4, 1\}\),其中 \(4\) 与 \(16\) 和 \(19\) 比 \(1\) 更近,所以 \(16\) 和 \(19\) 的 LCA 是 \(4\)。不难发现,两点的所有公共祖先中深度最大的与原两点距离最近。
证明:树上两点的所有公共祖先中深度最大的与原两点距离均最近
两个点的所有公共祖先都在一条从根节点出发的简单路径上,所以两点的所有公共祖先两两为祖先后代的关系,此时,深度加 $1$,与原两点的距离就分别加 $1$。所以原命题得证。于是,我们可以先处理出 \(u\) 的所有祖先,然后从 \(v\) 开始不断往父亲跳直到 \(u\) 的祖先中包含自己。需要注意,\(u\) 和 \(v\) 的 LCA 可以是 \(u\) 或 \(v\),例如此处 \(LCA(6,15)=6\)。对于查找,可以排序后二分,那么对于单次求 LCA 就是最坏 \(O(h\log h)\),其中 \(h\) 是树高,可以通过构造一条链使得 \(h=n\),于是这个算法对于单次求 LCA 是 \(O(n\log n)\) 的,可以通过原题 \(70\%\) 的数据。
代码示例
核心部分
def lca(u, v):
anc_v = [v]
while v != s:
v = fa[v]
anc_v.append(v)
anc_v.sort()
if contain(anc_v, u):
return u
while u != s:
u = fa[u]
if contain(anc_v, u):
return u
return -1
完整代码
n, m, s = map(int, input().split())
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
u, v = map(int, input().split())
g[u].append(v)
g[v].append(u)
fa = [0] * (n + 1)
def dfs(u, f):
fa[u] = f
for v in g[u]:
if v != f:
dfs(v, u)
dfs(s, 0)
for _ in range(m):
u, v = map(int, input().split())
print(lca(u, v))

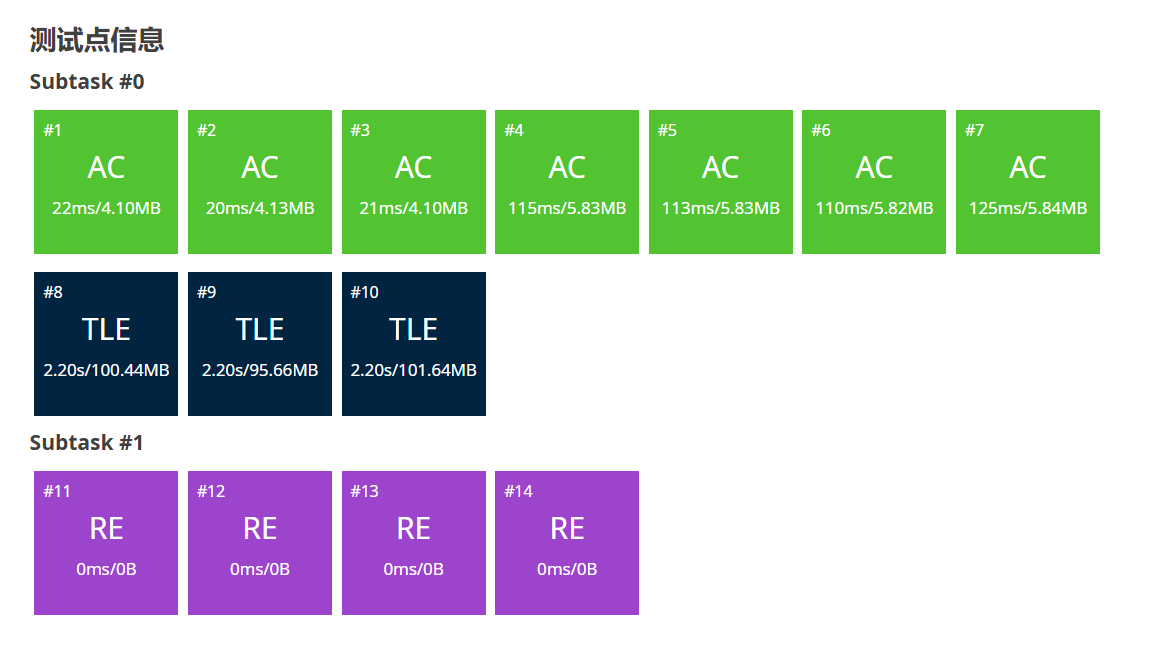
尝试优化我们的算法。可以发现,\(u\) 的所有祖先的深度都不小于(\(\geq\))\(u\) 的,于是对于求 \(u\) 和 \(v\) 的 LCA,可以先让深度较大者不断往父亲跳直到与另一个节点的深度相等。此时问题变成了求这两个深度相同的节点的 LCA,只要这两个点不相同,它们的 LCA 的深度就一定比它们的小,那么让两个节点向各自的父亲移动,重复直到它们重合就得到了答案。
例如此处求 \(15\) 和 \(19\) 的 LCA,先让 \(15\) 跳到 \(12\),此时 \(dep_{12}=dep_{19}\),然后 \(12\) 和 \(19\) 一起往上跳:\(12\Rightarrow6\),\(19\Rightarrow2\);\(6\Rightarrow3\),\(2\Rightarrow4\);\(3\Rightarrow1\),\(4\Rightarrow1\),于是 \(LCA(15, 19)=1\)。
那么我们得到了一个最坏 \(O(h)\) 的算法,同样可以构造链使得 \(h=n\),于是这个算法是单次查询 \(O(n)\) 的。对于题目仍然是 \(70\%\) 的数据,但时间会快许多。
代码示例
核心部分
def lca(u, v):
if dep[u] < dep[v]:
u, v = v, u
while dep[u] != dep[v]:
u = fa[u]
while u != v:
u, v = fa[u], fa[v]
return u
完整代码
n, m, s = map(int, input().split())
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
u, v = map(int, input().split())
g[u].append(v)
g[v].append(u)
fa, dep = [0] * (n + 1), [0] * (n + 1)
def dfs(u, f):
fa[u] = f
dep[u] = dep[f] + 1
for v in g[u]:
if v != f:
dfs(v, u)
dfs(s, 0)
def lca(u, v):
if dep[u] < dep[v]:
u, v = v, u
while dep[u] != dep[v]:
u = fa[u]
while u != v:
u, v = fa[u], fa[v]
return u
for _ in range(m):
u, v = map(int, input().split())
print(lca(u, v))
考虑优化。不难想到倍增。用倍增记录一个点向父亲跳二的整数幂次的结果,对于统一两点深度的操作,求深度差后拆分二进制即可。对于一起往上跳,从最高位开始,尝试将跳的次数的二进制中这一位设为 \(1\),如果跳后两个点重合,那么记录答案后将这一位设为 \(0\) 并进入下一位考虑;否则将这一位设为 \(1\) 后进入下一位。由于是从高位到低位尝试的,所以跳的层数一定是由大到小的,那么最后记录的答案一定是最优的。
具体实现
核心部分
def lca(u, v):
if dep[u] < dep[v]:
u, v = v, u
dep_diff = dep[u] - dep[v]
for i in range(k + 1):
if dep_diff & 1:
u = f[u][i]
dep_diff >>= 1
if u == v:
return u
ans = s
for i in reversed(range(k + 1)):
if f[u][i] == f[v][i]:
ans = f[u][i]
else:
u, v = f[u][i], f[v][i]
return ans
完整代码
import math
n, m, s = map(int, input().split())
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
u, v = map(int, input().split())
g[u].append(v)
g[v].append(u)
k = math.ceil(math.log2(n))
f = [[0]*(k+1) for _ in range(n + 1)]
dep = [0] * (n + 1)
def dfs(u, fa):
f[u][0] = fa
dep[u] = dep[fa] + 1
for v in g[u]:
if v != fa:
dfs(v, u)
dfs(s, s)
for i in range(1, k + 1):
for u in range(1, n + 1):
f[u][i] = f[f[u][i - 1]][i - 1]
def lca(u, v):
if dep[u] < dep[v]:
u, v = v, u
dep_diff = dep[u] - dep[v]
for i in range(k + 1):
if dep_diff & 1:
u = f[u][i]
dep_diff >>= 1
if u == v:
return u
ans = s
for i in reversed(range(k + 1)):
if f[u][i] == f[v][i]:
ans = f[u][i]
else:
u, v = f[u][i], f[v][i]
return ans
for _ in range(m):
u, v = map(int, input().split())
print(lca(u, v))

此处无法通过的原因是 Python 常数过大,用 C++ 之类的高效语言即可。
C++ 可通过代码
#include <bits/stdc++.h>
#define int long long
#define rep(i, l, r) for (int i = (l); i <= (r); ++ i)
#define per(i, l, r) for (int i = (l); i >= (r); -- i)
using namespace std;
constexpr int N = 5e5 + 10, K = 19;
int n, m, s, dep[N], f[N][K + 1];
vector <int> g[N];
void dfs(const int u, const int fa) {
f[u][0] = fa;
dep[u] = dep[fa] + 1;
for (const auto v: g[u]) {
if (v != fa) {
dfs(v, u);
}
}
}
int lca(int u, int v) {
if (dep[u] < dep[v]) {
swap(u, v);
}
int dep_diff = dep[u] - dep[v];
rep(i, 0, K) {
if (dep_diff & 1) {
u = f[u][i];
}
dep_diff >>= 1;
}
if (u == v) {
return u;
}
int ans = s;
per(i, K, 0) {
if (f[u][i] == f[v][i]) {
ans = f[u][i];
} else {
u = f[u][i], v = f[v][i];
}
}
return ans;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m >> s;
rep(i, 1, n - 1) {
int u, v;
cin >> u >> v;
g[u].emplace_back(v);
g[v].emplace_back(u);
}
dfs(s, s);
rep(i, 1, K) {
rep(u, 1, n) {
f[u][i] = f[f[u][i - 1]][i - 1];
}
}
rep(i, 1, m) {
int u, v;
cin >> u >> v;
cout << lca(u, v) << '\n';
}
return 0;
}

需要注意,这种写法并非最被广泛接受的做法,仅供参考。
思想介绍
言归正传,我们主要要了解的不是倍增。从另一个角度尝试优化暴力跳的做法。
要想缩减跳的次数,我们可以一次跳很多层但要保证跳完之后两点的 LCA 不变。不妨把跳的很多层视作从某祖先出发向下的一条链。不难想到,对于每个点预处理一个链头,链头从父亲开始不断向上跳,直到该点的父节点的儿子数量大于 \(1\),只要两个点不是祖先后代关系,那么这两个点分别跳到链头,它们的 LCA 不变。例如,\(16\) 的链头是 \(10\),\(15\) 的链头是 \(3\)。对于判断祖先后代关系,利用 dfs 序的性质即可,记录每个点的出入时间戳即可。
先放神秘代码再分析时间复杂度~
代码示例
n, m, s = map(int, input().split())
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
u, v = map(int, input().split())
g[u].append(v)
g[v].append(u)
dep, top = [0] * (n + 1), [0] * (n + 1)
dfn_in, dfn_out = [0] * (n + 1), [0] * (n + 1)
dfn_cnt = 0
def dfs(u, fa):
global dfn_cnt
dfn_cnt += 1
dfn_in[u] = dfn_cnt
dep[u] = dep[fa] + 1
num_sons = 0
for v in g[u]:
if v != fa:
num_sons += 1
for v in g[u]:
if v == fa:
continue
if num_sons == 1:
top[v] = top[u]
dfs(v, u)
else:
top[v] = u
dfs(v, u)
dfn_out[u] = dfn_cnt
top[s] = s
dfs(s, 0)
def lca(u, v):
while u != v:
if dep[u] < dep[v]:
u, v = v, u
if dfn_in[v] < dfn_in[u] <= dfn_out[v]:
return v
u = top[u]
return u
for _ in range(m):
u, v = map(int, input().split())
print(lca(u, v))
C++ 代码
#include <bits/stdc++.h>
#define int long long
#define rep(i, l, r) for (int i = (l); i <= (r); ++ i)
#define per(i, l, r) for (int i = (l); i >= (r); -- i)
using namespace std;
constexpr int N = 5e5 + 10, K = 19;
int n, m, s, dep[N], top[N], dfn_in[N], dfn_out[N], dfn_cnt;
vector <int> g[N];
void dfs(const int u, const int fa) {
dfn_in[u] = ++ dfn_cnt;
dep[u] = dep[fa] + 1;
int num_sons = 0;
for (const auto v: g[u]) {
if (v != fa) {
++ num_sons;
}
}
for (const auto v: g[u]) {
if (v == fa) {
continue;
}
if (num_sons == 1) {
top[v] = top[u];
dfs(v, u);
} else {
top[v] = u;
dfs(v, u);
}
}
dfn_out[u] = dfn_cnt;
}
int lca(int u, int v) {
while (u != v) {
if (dep[u] < dep[v]) {
swap(u, v);
}
if (dfn_in[v] < dfn_in[u] && dfn_in[u] <= dfn_out[v]) {
return v;
}
u = top[u];
}
return u;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m >> s;
rep(i, 1, n - 1) {
int u, v;
cin >> u >> v;
g[u].emplace_back(v);
g[v].emplace_back(u);
}
top[s] = s;
dfs(s, 0);
rep(i, 1, m) {
int u, v;
cin >> u >> v;
cout << lca(u, v) << '\n';
}
return 0;
}

显然实际结果出人意料(但最后一个点卡不过去,而且还有 subtasks 呢)。不妨让我们试着分析一下。
对于链树显然它是 \(O(1)\) 的,对于完全二叉树显然是 \(O(\log n)\)。对于这种算法直接分析时间复杂度比较复杂,所以我们只需要卡它就行了。本质是要构造一个二叉树,具体如下图。
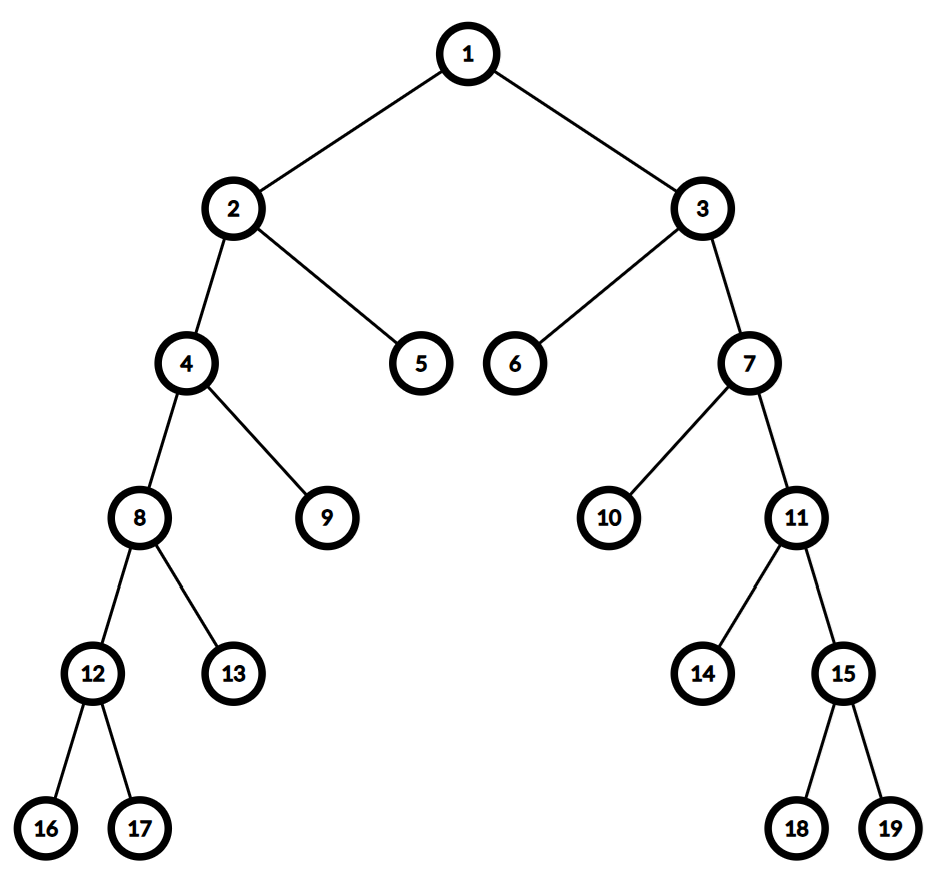
求 \(16\) 和 \(19\) 的 LCA 就能把单次查询卡到 \(O(n)\) 的,对于更大的 \(n\) 以此类推。但是在随机树上它的表现很惊人,简直就是 SPFA 再世。
到这一步,已经离我们的正解很接近了。上面划分重儿子的方式使得当 \(u\) 和 \(v\) 非祖先后代关系时,它们各自跳到链头后 LCA 不变,因此对于谁优先跳的要求很宽松。但如果两个点都跳之后 LCA 不变,无论是什么划分重儿子方式都会被上图卡掉。所以我们不妨划分:只让 \(u\) 和 \(v\) 中的至少一个跳链后它们的 LCA 不变。不难想到,让链头深度较大(即链头靠下)的那个节点跳链。
那么对于划分重儿子的方法,可以猜一下:以最深的子树作为重儿子。
完整代码
n, m, s = map(int, input().split())
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
u, v = map(int, input().split())
g[u].append(v)
g[v].append(u)
fa, dep, son, top = [0] * (n + 1), [0] * (n + 1), [0] * (n + 1), [0] * (n + 1)
def dfs1(u, f):
dep[u] = dep[f] + 1
fa[u] = f
max_h = 0
for v in g[u]:
if v == f:
continue
h_v = dfs1(v, u)
if h_v > max_h:
max_h, son[u] = h_v, v
return max_h + 1
dfs1(s, 0)
def dfs2(u, tp):
top[u] = tp
for v in g[u]:
if v != fa[u]:
if v == son[u]:
dfs2(v, tp)
else:
dfs2(v, v)
dfs2(s, s)
def lca(u, v):
while top[u] != top[v]:
if dep[top[u]] < dep[top[v]]:
u, v = v, u
u = fa[top[u]]
return u if dep[u] < dep[v] else v
for _ in range(m):
u, v = map(int, input().split())
print(lca(u, v))
C++ 可通过代码
#include <bits/stdc++.h>
#define int long long
#define rep(i, l, r) for (int i = (l); i <= (r); ++ i)
#define per(i, l, r) for (int i = (l); i >= (r); -- i)
using namespace std;
constexpr int N = 5e5 + 10;
int n, m, s, fa[N], dep[N], son[N], top[N];
vector <int> g[N];
int dfs(const int u) {
dep[u] = dep[fa[u]] + 1;
int max_h = 0;
for (const auto v: g[u]) {
if (v == fa[u]) {
continue;
}
fa[v] = u;
const int h_v = dfs(v);
if (h_v > max_h) {
max_h = h_v, son[u] = v;
}
}
return max_h + 1;
}
void dfs(const int u, const int tp) {
top[u] = tp;
for (const auto v: g[u]) {
if (v == fa[u]) {
continue;
}
if (v == son[u]) {
dfs(v, tp);
} else {
dfs(v, v);
}
}
}
int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) {
swap(u, v);
}
u = fa[top[u]];
}
return dep[u] < dep[v] ? u : v;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m >> s;
rep(i, 1, n - 1) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(s), dfs(s, s);
rep(i, 1, m) {
int u, v;
cin >> u >> v;
cout << lca(u, v) << '\n';
}
return 0;
}

对于为什么这个算法能通过,我们先证明正确性,再分析时间复杂度。
正确性证明
设有两点 $u$ 和 $v$,它们的 LCA 是 $w$。- \(top_u=top_v\):此时 \(u\) 和 \(v\) 在同一条长链上,即它们为祖先后代关系,取深度较小者作为答案 \(w\) 是正确的。
- \(top_u\neq top_v\):此时取链头深度较大即链头较深者跳,肯定会跳到 \(w\) 及以下的节点,因为如果 \(u\) 跳到了 \(w\) 及以上的节点,说明 \(w\) 的重儿子一定是在 \(u->w\) 的路径上的,此时 \(v\) 的链头一定在 \(w\) 下面,此时跳 \(u\) 是不合理的。注意,此时 \(u\) 和 \(v\) 可能是祖先后代关系,这时候跳链的一定是后代,正确性不变。
至此,我们可以发现正确性和重儿子选择的方式无关。
时间复杂度分析
直接往最坏情况考虑。由于时间复杂度分析不带常数,所以不妨直接考虑从叶子跳到根最多要跳链多少次。最大化这个答案,构造数据去卡即可。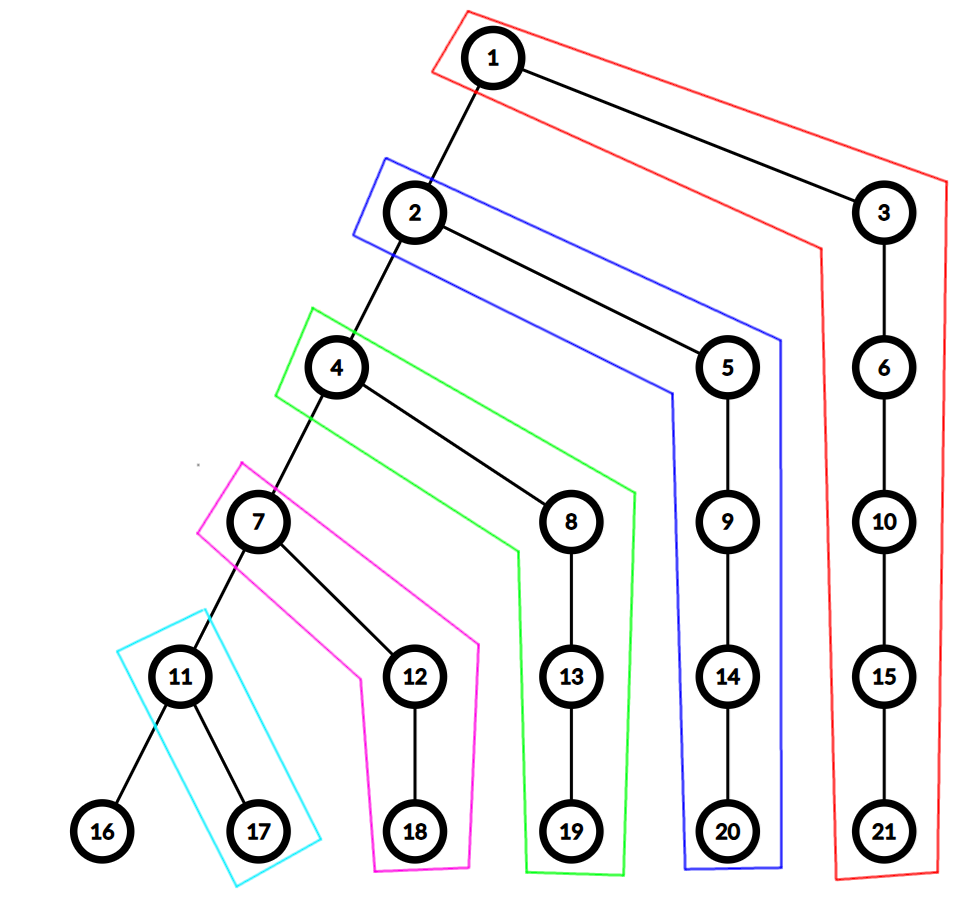
根据图片不难看出,这个剖法是单次查询 \(O(n\sqrt{n})\) 的,正好能够通过这道题。
那么,现在我们得到了一个预处理 \(O(n)\),单次查询 \(O(\sqrt{n})\) 的。虽说预处理比倍增快,但查询时间差强人意。所以我们现在考虑优化重儿子划分的方法。
重链剖分
在跳链的过程中,我们发现会跳过一些不在 \(u\) 和 \(v\) 之间路径上点。我们需要做的是最大化跳过的点的数量。上面的做法是选择最高的子树作为重儿子,那么换成最重(后代最多)的子树,就能最大化跳过的点的数量。这就是重链剖分,而上面的做法就是长链剖分。代码几乎只有 dfs1 函数发生了改变。
重链就是每个点到重儿子的边组成的链。
完整代码
n, m, s = map(int, input().split())
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
u, v = map(int, input().split())
g[u].append(v)
g[v].append(u)
fa, dep, son, top = [0] * (n + 1), [0] * (n + 1), [0] * (n + 1), [0] * (n + 1)
def dfs1(u, f):
dep[u] = dep[f] + 1
fa[u] = f
maxs, size = 0, 1
for v in g[u]:
if v == f:
continue
s_v = dfs1(v, u)
if s_v > maxs:
maxs, son[u] = s_v, v
size += s_v
return size
dfs1(s, 0)
def dfs2(u, tp):
top[u] = tp
for v in g[u]:
if v != fa[u]:
if v == son[u]:
dfs2(v, tp)
else:
dfs2(v, v)
dfs2(s, s)
def lca(u, v):
while top[u] != top[v]:
if dep[top[u]] < dep[top[v]]:
u, v = v, u
u = fa[top[u]]
return u if dep[u] < dep[v] else v
for _ in range(m):
u, v = map(int, input().split())
print(lca(u, v))
C++ 可通过代码
#include <bits/stdc++.h>
#define int long long
#define rep(i, l, r) for (int i = (l); i <= (r); ++ i)
#define per(i, l, r) for (int i = (l); i >= (r); -- i)
using namespace std;
constexpr int N = 5e5 + 10;
int n, m, s, fa[N], dep[N], son[N], top[N];
vector <int> g[N];
int dfs(const int u) {
dep[u] = dep[fa[u]] + 1;
int maxs = 0, ret = 1;
for (const auto v: g[u]) {
if (v == fa[u]) {
continue;
}
fa[v] = u;
const int sz = dfs(v);
if (sz > maxs) {
maxs = sz;
son[u] = v;
}
ret += sz;
}
return ret;
}
void dfs(const int u, const int tp) {
top[u] = tp;
for (const auto v: g[u]) {
if (v == fa[u]) {
continue;
}
if (v == son[u]) {
dfs(v, tp);
} else {
dfs(v, v);
}
}
}
int lca(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) {
swap(u, v);
}
u = fa[top[u]];
}
return dep[u] < dep[v] ? u : v;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m >> s;
rep(i, 1, n - 1) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs(s), dfs(s, s);
rep(i, 1, m) {
int u, v;
cin >> u >> v;
cout << lca(u, v) << '\n';
}
return 0;
}

由于每次跳链至少会跳过同等与目前子树大小个点,所以这个算法是单次查询 \(O(\log n)\) 的,而且完全跑不满。
那么重链剖分就只有这么点用吗?当然不是!观察求 LCA 的函数,两点在跳的过程中覆盖的点,正好就是两点之间的路径!
看这样一道题。
子树操作让我们想到 dfs 序,众所周知,子树中每个节点在 dfs 序上正好是一个区间。对于链,让所有从根出发的链的 dfs 序都组成一个区间是不可能的,所以我们不妨让每一条重链上的 dfs 序连续,从而将两点间路径需要用到的区间数量控制在 \(2\log n\) 以内。要让重链上的 dfs 序连续,在标记 dfs 序时优先遍历重儿子即可。至于维护区间,把线段树甩过去就行了。那么路径修改与查询就是 \(O(\log^2n)\) 的。
完整代码
class sgt:
def __init__(self, _n, _p, _a):
self._n, self._p, self._t, self._lazy = _n, _p, [0] * _n * 4, [0] * _n * 4
self._build(1, 1, _n, _a)
def _push_up(self, now):
self._t[now] = (self._t[now * 2] + self._t[now * 2 + 1]) % self._p
def _build(self, now, tl, tr, _a):
if tl == tr:
self._t[now] = _a[tl] % self._p
return
mid = (tl + tr) // 2
self._build(now * 2, tl, mid, _a)
self._build(now * 2 + 1, mid + 1, tr, _a)
self._push_up(now)
def _add(self, now, tl, tr, _x):
self._t[now] = (self._t[now] + _x * (tr - tl + 1)) % self._p
self._lazy[now] = (self._lazy[now] + _x) % self._p
def _push_down(self, now, tl, tr):
if self._lazy[now]:
mid = (tl + tr) // 2
self._add(now * 2, tl, mid, self._lazy[now])
self._add(now * 2 + 1, mid + 1, tr, self._lazy[now])
self._lazy[now] = 0
def _modify_add(self, now, tl, tr, l, r, _x):
if l <= tl <= tr <= r:
self._add(now, tl, tr, _x)
return
self._push_down(now, tl, tr)
mid = (tl + tr) // 2
if l <= mid:
self._modify_add(now * 2, tl, mid, l, r, _x)
if r > mid:
self._modify_add(now * 2 + 1, mid + 1, tr, l, r, _x)
self._push_up(now)
def _query_sum(self, now, tl, tr, l, r):
if l <= tl <= tr <= r:
return self._t[now]
self._push_down(now, tl, tr)
mid = (tl + tr) // 2
if r <= mid:
return self._query_sum(now * 2, tl, mid, l, r)
elif l > mid:
return self._query_sum(now * 2 + 1, mid + 1, tr, l, r)
else:
return (self._query_sum(now * 2, tl, mid, l, r) + self._query_sum(now * 2 + 1, mid + 1, tr, l, r)) % self._p
def modify_add(self, l, r, _x): self._modify_add(1, 1, self._n, l, r, _x)
def query_sum(self, l, r): return self._query_sum(1, 1, self._n, l, r)
class hld:
def __init__(self, _n, _s, _p, _a, _e):
self._n, self._s, self._p = _n, _s, _p
org_a = [0] * (_n + 1)
self._fa = [0] * (_n + 1)
self._dep = [0] * (_n + 1)
self._son = [0] * (_n + 1)
self._top = [0] * (_n + 1)
self._dfn = [0] * (_n + 1)
self._dfn_out = [0] * (_n + 1)
self._dfn_cnt = 0
self._g = [[] for _ in range(_n + 1)]
for u, v in _e:
self._g[u].append(v)
self._g[v].append(u)
self._dfs1(_s)
self._dfs2(_s, _s)
for i in range(1, _n + 1):
org_a[self._dfn[i]] = _a[i]
self._sgt = sgt(_n, _p, org_a)
def _dfs1(self, u):
self._dep[u] = self._dep[self._fa[u]] + 1
maxs, size = 0, 1
for v in self._g[u]:
if v == self._fa[u]:
continue
self._fa[v] = u
s_v = self._dfs1(v)
if s_v > maxs:
maxs, self._son[u] = s_v, v
size += s_v
return size
def _dfs2(self, u, tp):
self._top[u] = tp
self._dfn_cnt += 1
self._dfn[u] = self._dfn_cnt
if self._son[u]:
self._dfs2(self._son[u], tp)
for v in self._g[u]:
if v != self._fa[u] and v != self._son[u]:
self._dfs2(v, v)
self._dfn_out[u] = self._dfn_cnt
def path_modify_add(self, u, v, _x):
while self._top[u] != self._top[v]:
if self._dep[self._top[u]] < self._dep[self._top[v]]:
u, v = v, u
self._sgt.modify_add(self._dfn[self._top[u]], self._dfn[u], _x)
u = self._fa[self._top[u]]
if self._dep[u] > self._dep[v]:
u, v = v, u
self._sgt.modify_add(self._dfn[u], self._dfn[v], _x)
def path_query_sum(self, u, v):
ans = 0
while self._top[u] != self._top[v]:
if self._dep[self._top[u]] < self._dep[self._top[v]]:
u, v = v, u
ans = (ans + self._sgt.query_sum(self._dfn[self._top[u]], self._dfn[u])) % self._p
u = self._fa[self._top[u]]
if self._dep[u] > self._dep[v]:
u, v = v, u
ans = (ans + self._sgt.query_sum(self._dfn[u], self._dfn[v])) % self._p
return ans
def subtree_modify_add(self, u, _x):
self._sgt.modify_add(self._dfn[u], self._dfn_out[u], _x)
def subtree_query_sum(self, u):
return self._sgt.query_sum(self._dfn[u], self._dfn_out[u])
n, m, s, p = map(int, input().split())
a, e = [0] + list(map(int, input().split())), []
for _ in range(n - 1):
e.append(tuple(map(int, input().split())))
hld = hld(n, s, p, a, e)
for _ in range(m):
match list(map(int, input().split())):
case [1, x, y, z]:
hld.path_modify_add(x, y, z)
case [2, x, y]:
print(hld.path_query_sum(x, y))
case [3, x, z]:
hld.subtree_modify_add(x, z)
case [4, x]:
print(hld.subtree_query_sum(x))
C++ 可通过代码
#include <bits/stdc++.h>
#define int long long
#define rep(i, l, r) for (int i = (l); i <= (r); ++ i)
#define per(i, l, r) for (int i = (l); i >= (r); -- i)
#define pp pair <int, int>
using namespace std;
constexpr int N = 1e5 + 10;
int n, m, root, p, a[N], org[N], dfn[N], dfn_end[N], dfncnt;
int fa[N], dep[N], son[N], top[N];
int t[N * 4], tag[N * 4];
vector <int> g[N];
int dfs1(const int u) {
dep[u] = dep[fa[u]] + 1;
int ret = 1, maxs = 0, maxn = 0;
for (const auto v : g[u]) {
if (v != fa[u]) {
fa[v] = u;
const int sz = dfs1(v);
if (sz > maxs) {
maxs = sz;
maxn = v;
}
ret += sz;
}
}
son[u] = maxn;
return ret;
}
void dfs2(const int u, const int tp) {
top[u] = tp;
dfn[u] = ++ dfncnt;
org[dfn[u]] = a[u];
if (son[u]) {
dfs2(son[u], tp);
}
for (const auto v : g[u]) {
if (v != fa[u] && v != son[u]) {
dfs2(v, v);
}
}
dfn_end[u] = dfncnt;
}
void push_up(const int now) {
t[now] = (t[now * 2] + t[now * 2 + 1]) % p;
}
void add(const int now, const int tl, const int tr, const int x) {
t[now] = (t[now] + (tr - tl + 1) * x % p) % p;
tag[now] = (tag[now] + x) % p;
}
void push_down(const int now, const int tl, const int tr) {
if (tag[now]) {
const int mid = (tl + tr) / 2;
add(now * 2, tl, mid, tag[now]);
add(now * 2 + 1, mid + 1, tr, tag[now]);
tag[now] = 0;
}
}
void build(const int now, const int tl, const int tr) {
if (tl == tr) {
t[now] = (org[tl] % p + p) % p;
return ;
}
const int mid = (tl + tr) / 2;
build(now * 2, tl, mid);
build(now * 2 + 1, mid + 1, tr);
push_up(now);
}
void modify(const int now, const int tl, const int tr, const int l, const int r, const int x) {
if (tl >= l && tr <= r) {
add(now, tl, tr, x);
return ;
}
if (tl > r || tr < l) {
return ;
}
push_down(now, tl, tr);
const int mid = (tl + tr) / 2;
modify(now * 2, tl, mid, l, r, x);
modify(now * 2 + 1, mid + 1, tr, l, r, x);
push_up(now);
}
int query(const int now, const int tl, const int tr, const int l, const int r) {
if (tl >= l && tr <= r) {
return t[now];
}
push_down(now, tl, tr);
const int mid = (tl + tr) / 2;
if (r <= mid) {
return query(now * 2, tl, mid, l, r);
}
if (l > mid) {
return query(now * 2 + 1, mid + 1, tr, l, r);
}
return (query(now * 2, tl, mid, l, r)
+ query(now * 2 + 1, mid + 1, tr, l, r)) % p;
}
void modify_path(int u, int v, const int x) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) {
swap(u, v);
}
modify(1, 1, n, dfn[top[u]], dfn[u], x);
u = fa[top[u]];
}
if (dep[u] > dep[v]) {
swap(u, v);
}
modify(1, 1, n, dfn[u], dfn[v], x);
}
int query_path(int u, int v) {
int ret = 0;
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]]) {
swap(u, v);
}
ret = (ret + query(1, 1, n, dfn[top[u]], dfn[u])) % p;
u = fa[top[u]];
}
if (dep[u] > dep[v]) {
swap(u, v);
}
ret = (ret + query(1, 1, n, dfn[u], dfn[v])) % p;
return ret;
}
void modify_subtree(const int u, const int x) {
modify(1, 1, n, dfn[u], dfn_end[u], x);
}
int query_subtree(const int u) {
return query(1, 1, n, dfn[u], dfn_end[u]);
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m >> root >> p;
rep(i, 1, n) {
cin >> a[i];
}
rep(i, 1, n - 1) {
int u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
dfs1(root);
dfs2(root, root);
build(1, 1, n);
while (m --) {
int opt;
cin >> opt;
if (opt == 1) {
int u, v, x;
cin >> u >> v >> x;
modify_path(u, v, x);
} else if (opt == 2) {
int u, v;
cin >> u >> v;
cout << query_path(u, v) << '\n';
} else if (opt == 3) {
int u, x;
cin >> u >> x;
modify_subtree(u, x);
} else {
int u;
cin >> u;
cout << query_subtree(u) << '\n';
}
}
return 0;
}

重剖+线段树的题非常多,但其实都是一个板子,大部分真正考的是线段树,意义不大,做几道就完了。
需要注意的是,有的题对于信息合并的要求比较高,例如这道题的信息合并需要两端区间连续且方向相同,需要多注意。
至此,重链剖分就完结撒花。
长链剖分
还记得我们一开始想到的取最高的子树为重儿子的剖法吗?它就是长链剖分。
树上 \(k\) 级祖先 就是长链剖分一个典型的用武之地。
显然有倍增 \(O(n\log n)\) 预处理、\(O(\log n)\) 单次查询的做法。此处我们想让单次查询变成 \(O(1)\) 的。
既然是 \(k\) 级祖先,那先跳一部分再说。C++ 中对于整数求 \(\lfloor\log_2x\rfloor\) 的函数 __lg() 是 \(O(1)\) 的。令 \(h=2^{\lfloor\log_2k\rfloor}\),先用倍增向上跳 \(h\) 次(这个过程是 \(O(1)\) 的),那么剩下的就是 \(k-h\) 层,显然 \(k-h<h\)。设原先的点为 \(u\),规定节点 \(u\) 的 \(k\) 级祖先是 \(fa_k(u)\)。我们需要利用的性质是从 \(fa_k(u)\) 出发往下的长链长度(此处规定为经过的节点数)不小于 \(k\)。当 \(u\) 在这条长链上时显然成立,否则说明 \(fa_k(u)\) 有一个不会更矮的子树,结论依旧成立。那这个性质有什么用呢?我们记录每条长链上的点和根节点上面与链长数量相等数量的所有点,对于求 \(fa_k(u)\),先向上跳 \(h\) 层,得到 \(fa_h(u)\),再找到 \(fa_h(u)\) 所处长链的链头,然后根据链头深度与 \(dep_u+k\) 的关系考虑是取链头上面的第几个点或是链头下面的第几个点。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号