乱谈斜率优化 & 李超线段树
上课讲的时候都听不懂,下课之后还花了若干个小时。我怎么这么菜?我怎么这么菜?我怎么这么菜?
斜率优化
引入
我们在处理各种东西是,难免会遇到这个问题:
问题:我们要计算 \(\max_{1\le j<i \le n}(A(i) \times B(j)+C(i)+D(j)+E)\) 这个式子或是 \(\min_{1\le j<i \le n}(A(i) \times B(j)+C(i)+D(j)+E)\) 这个式子,其中 \(A,B,C,D\) 都是函数,而且互相都是独立的,\(E\) 是常数。
容易发现我们的数据结构维护或者是其他方法都很难处理,即使能处理也只能处理简单的情况。但是,这个问题就可以被斜率优化解决。
注意,前面这个要计算的式子只能是外面套一个最值,然后里面是两个东西相乘再加上两个东西相加再加上一个常数。如果不是这个形式,就不能用斜率优化。
不妨设 \(A,B,C,D,E\) 的计算都是 \(O(1)\) 的,显然这个式子可以平方算法来解决。而斜率优化可以更快的解决。(具体时间复杂度要看单调性而定,后面会讲)
思路
斜率优化的第一步还是先枚举 \(i\)。然后我们就可以计算 \(A(i)\) 和 \(C(i)\) 了,剩下还剩 \(B(i)\) 和 \(D(i)\)。
然后我们就需要想,如何快速计算 \(i\) 对应的最优的 \(j\)。显然 \(E+C(i)\) 可以在最终要计算出答案时再加上,所以就相当于求出 \(B(i) \times A(i)+D(i)\) 的最值。
注意到这个式子很像一个一次函数,所以考虑数形结合,令 \(k=-A(i),x(j)=B(j),y(j)=D(j)\)。然后改个名字,我们要计算的就变成了 \(y(j)-k \times x(j)\) 的最值。(其中 \(1 \le j< i \le n\))
然后再想回一次函数的 \(y-kx\),你能发现什么?
学过函数的应该都知道,这就是 \(b=y-kx\),一次函数的斜截式。
所以这就变成了,有一堆二维平面的点 \((x_j,y_j)(1 \le j < i)\),然后你需要在其中选一个 \(j\),使得 \(y(j)-k \times x(j)\) 最小,也就是 \(y(j)=k \times x(j)+b\) 的截距最小,也就是说,经过 \((x_j,y_j)\) 这个点的斜率为 \(k\) 的直线的截距最小。
然后我们知道 \(k\) 不变,也就是一次函数的斜率不变,也就是说,对于 \(i\) 固定的所有 \(j\),所有的不同只有截距不同。
(斜率优化,之所以是因为发现了对于 \(i\) 所有的 \(j\) 对应的直线的斜率都一样,才叫做“斜率优化”。)
在之后,我们只考虑 \(\min\)。容易发现 \(\max\) 的情况和 \(\min\) 是差不多的,也就是反过来一下而已。
考虑数形结合。虽然我们目前不太知道机器该怎么解决,但是人为判断还是可以的。
那我们先画出来 \(1 \sim i-1\) 的位置中所有的点。
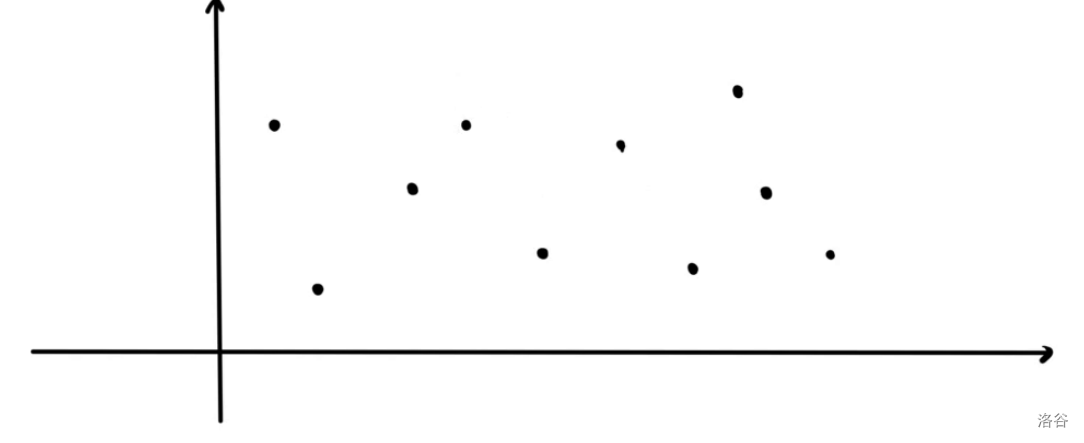
那我们怎么对于一个 \(i\),计算最小截距呢?
这时候假设我们有一条直线,我们只需要把这条直线放在最下方,然后一直往上挪挪挪,一直平移直到碰到点为止。这时候的点就一定是答案的点。(也就是截距最小)
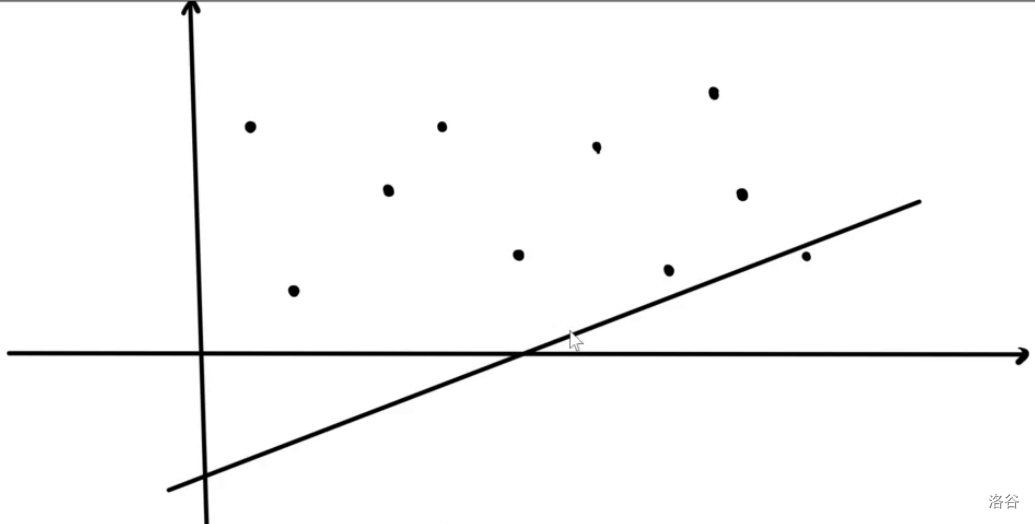
我们不难发现,无论是什么斜率的直线,从最底下开始平移,最终可能第一个碰到的点的集合,就是下凸包的点集。
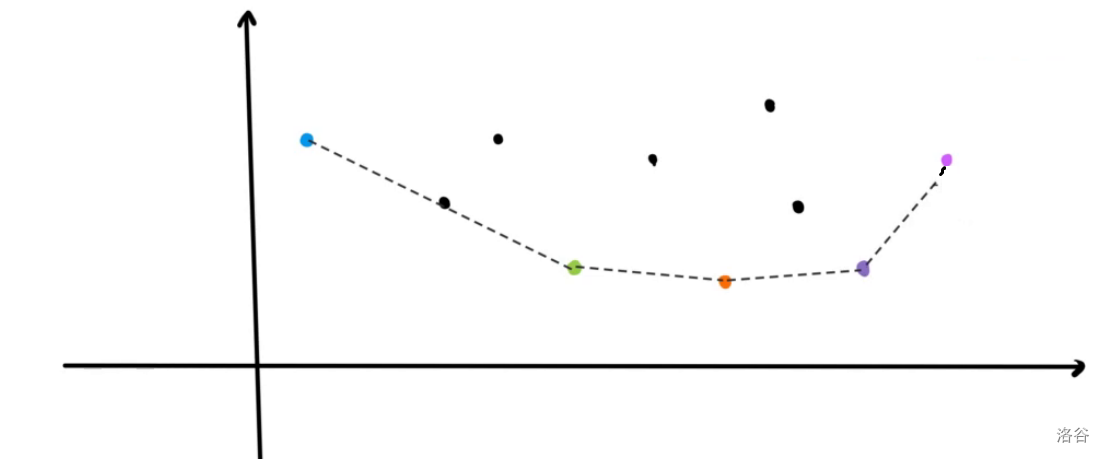
同理,如果我们要取得是 \(\max\),就是上凸包。
于是我们就发现,对于 \(1 \sim i-1\) 的点,只有下凸包上面的点,才有可能成为最终的决策点。
而我们还可以发现,如果一个点不再属于下凸包的点集,之后也不会属于。所以这是一个类似单调栈的情况。
我们将凸包中相邻的点两两连线。于是我们就会发现这些直线的斜率单调上升。
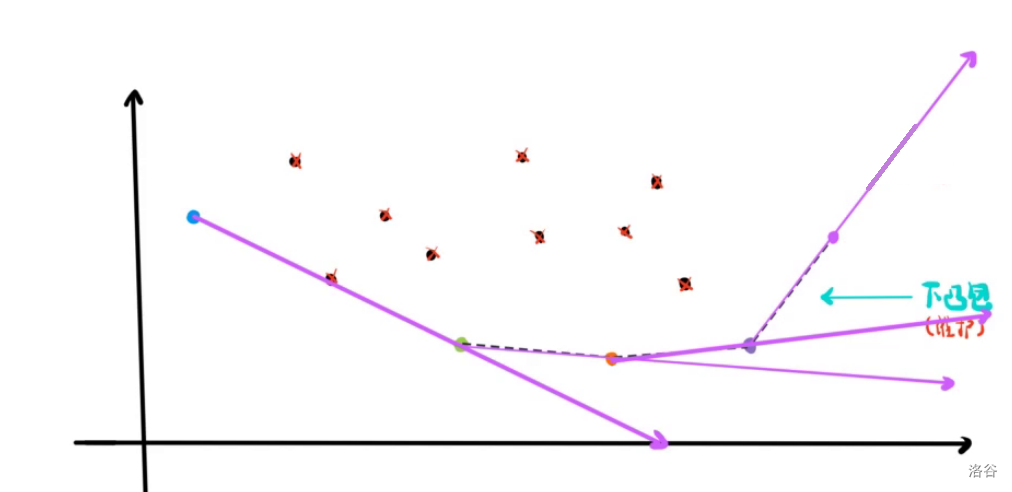
单调上升你就发现,可以直接二分最佳决策点。
怎么个二分法呢?我们考虑一条直线。这条直线如果第一个碰到了某一个点,则这个点和左边的点的直线的斜率小于它,而和右边的点的直线的斜率大于它。所以我们还需要一个 \(O(\log n)\)。
于是,求解答案的部分就解决了。
怎么维护下凸包呢?我们一开始有一个比较 naive 的方法:只需要使用单调栈 \(O(n)\) 维护即可。
具体怎么维护,就是在加入一个点之前,先比较一下和单调栈顶上的两个点的斜率的大小关系,如果就发现可以被替换掉就把栈弹出即可。
就比如:
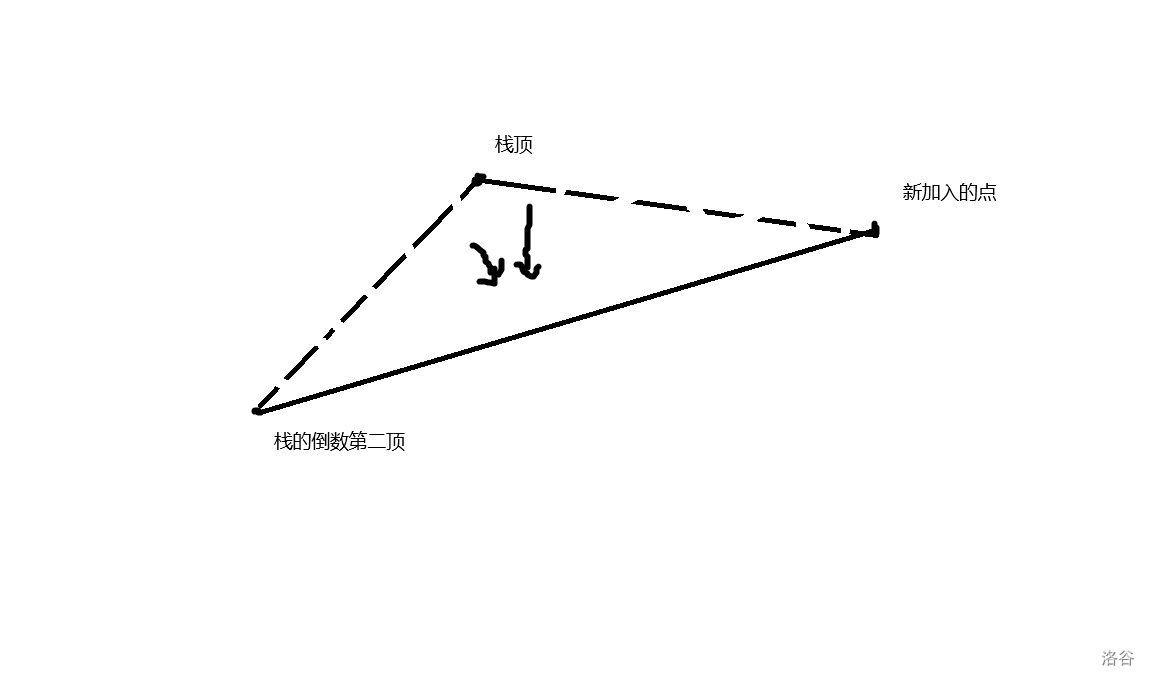
这样就要弹出栈顶。
而且还有一个细节:如果 \(x\) 相等的话,就需要取最下面的点作为凸包上的点。
但是,这并不对。
这种方法只能维护在左边或者是右边插入的情况,如果在中间插入呢?
因此,我们需要分类讨论一下单调性。
(查询)斜率单调,横坐标单调
因为查询的直线斜率单调,所以,每一个最优的决策点一定是从左往右的。\(O(n)\)。
而因为横坐标单调,我们还是可以直接使用单调栈的方法维护下凸包。\(O(n)\)。
总复杂度线性。
(查询)斜率不单调,横坐标单调
查询就可以使用二分了。而横坐标还是直接线性即可。
总复杂度 \(O(n \log n)\)。
(查询)斜率单调,横坐标不单调
李超线段树显然是一种做法,但是如果存在更加优秀的做法,会在后文提到。
(查询)斜率不单调,横坐标不单调
也可以李超线段树,会在后文提到。
斜率优化 DP
顾名思义就是使用斜率优化来优化 DP。
实际上,斜率优化 DP 就是将
变成了
(这里我们仍然只考虑最小值的情况,最大值和最小值是差不多的。)
又因为 \(i\) 是定值:
但是 \(D(j)\) 这时候还有点累赘。所以考虑 \(\forall 1 \le i \le n,D(i)+dp_i \to D_i\)。
得到
与此同时,最终得到答案的时候也不要忘记 \(-D(i)\)!!
于是我们的目标还是求解 \(\min_{1\le j<i \le n}(D(j)+A(i) \times B(j))\),直接使用前面讲过的方法即可。
但是还会有几种奇怪的式子,但是也就是加上一点点变数,改改也可以做。
例如这个式子:
也可以通过乘法分配律变成:
于是也可以斜率优化。
但是在这里还是介绍一个小 tips,如何判断一个转移方程可以使用斜率优化:
把右边和 \(j\) 无关的项丢到外面,把只和 \(j\) 有关的数放在一起(\(D(j)\)),\(i,j\) 同时有关的项放一起得到 \(U(i,j)\)。
如果 \(U(i,j)\) 可以表示成 \(A(i) \times B(j)\) 的形式,那么可以斜率优化。
斜率优化 DP 板子
声明:该板子只能用于横坐标单调的情况,横坐标不单调的情况会在后面说。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define N 100010
int n, s, t, c, sumt[N], sumc[N], que[N], dp[N];
int Y(int p) {
return ???;
}
int X(int p) {
return ???;
}
int K(int p) {
return ???;
}
bool cmp1(int a, int b, int k) {
return (Y(b) - Y(a)) ??? k * (X(b) - X(a));
}
bool cmp2(int a, int b, int c) {
return (Y(b) - Y(a)) * (X(c) - X(b)) ??? (Y(c) - Y(b)) * (X(b) - X(a));
}
void cal(int x, int y) {
dp[x] = dp[y] + ???;
}
int binary_search(int left, int right, int k) {
int res = right ;
while (left <= right) {
int mid = (left + right) >> 1;
if (cmp1(que[mid], que[mid + 1], k) == ??? )
left = mid + 1;
else
right = mid - 1, res = mid;
}
return que[res];
}
int work() {
que[1] = dp[0] = 0;
for (int i = 1, head = 1, tail = 1; i <= n; ++i) {
cal(i, binary_search(head, tail, K(i)));
while (head < tail && cmp2(que[tail - 1], que[tail], i) == true)
--tail;
que[++tail] = i;
}
return dp[n];
}
我将分段解析。
int Y(int p) {
return ???;
}
int X(int p) {
return ???;
}
int K(int p) {
return ???;
}
这里就是三个式子。分些用来计算纵坐标、横坐标和斜率。
bool cmp1(int a, int b, int k) {
return (Y(b) - Y(a)) ??? k * (X(b) - X(a));
}
bool cmp2(int a, int b, int c) {
return (Y(b) - Y(a)) * (X(c) - X(b)) ??? (Y(c) - Y(b)) * (X(b) - X(a));
}
void cal(int x, int y) {
dp[x] = dp[y] + ???;
}
cmp1 是斜率和直线斜率的比较。
cmp2 是直线之间斜率的比较。
里面的式子可以通过数学推导得到,但是注意要使用 int128。
cal 函数就是用来 DP 转移的。
这里就还有一个小细节:cmp1 和 cmp2 中最好写 <= 或是 >=,为的是防止一些奇怪的情况,比如说 x 相等。
int work() {
que[1] = dp[0] = 0;
for (int i = 1, head = 1, tail = 1; i <= n; ++i) {
cal(i, binary_search(head, tail, K(i)));
while (head < tail && cmp2(que[tail - 1], que[tail], i) == true)
--tail;
que[++tail] = i;
}
return dp[n];
}
que, head, tail 都是用来模拟单调队列的。
先循环 \(i\)。然后就是三步:
- 对于 \(i\) 二分找到最优决策点 \(j\)。并完成转移。
- 尝试将 \(i\) 加入半凸包(这里是上凸包还是下凸包我也不清楚,需要按照题目来定)。弹出所有不合法的点。
- 加入半凸包。
int binary_search(int left, int right, int k) {
int res = right ;
while (left <= right) {
int mid = (left + right) >> 1;
if (cmp1(que[mid], que[mid + 1], k) == ??? )
left = mid + 1;
else
right = mid - 1, res = mid;
}
return que[res];
}
很多人这里二分查找会出错,这里的细节真的应该好好看看。
首先是 res = right。这是说我们默认了 right 是当前的最优值。为啥呢?因为你每次遇到一个合法点都会 res = mid,最后 res 保存的就是最小的合法点。而我们又知道 right 肯定是一个合法点(因为不存在 right + 1 的位置,也不会存在 right 和 right + 1 之间的边),所以一开始就可以设 res = right。
还有一个细节,就是 que[mid] 和 que[mid + 1]。因为 mid 是一个单调队列中的位置,需要在单调队列中找到对应的数。
细节
一共有好几个细节。
- \(x(j)\) 不是严格单调的,需要考虑 \(x(j_1) = x(j_2)\) 的特殊情况。
- 注意使用
__int128,无论是否爆了long long,都会返回合法的 \(j\)。 - 建议用
<=或>=。 - 如果斜率用浮点表示,记得用
long double。 - 初始决策点的加入根据具体问题考虑。
斜率优化本来就稍微偏板子,所以例题不多讲了。
李超线段树
因为是笔者自己记录的东西,所以就直接挂个地址吧。
https://www.cnblogs.com/Shinomiya/p/15560042.html
自已一定要多看!
实际上,李超线段树实际上就是一个分类讨论。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号