浅谈李超线段树实现斜率优化dp

浅谈李超线段树实现斜率优化dp

李超线段树

先来看一道例题：

[HEOI2013]Segment

要求在平面直角坐标系下维护两个操作：

  1. 在平面上加入一条线段 \((x_1,y_1)\rightarrow (x_2,y_2)\)。记第 \(i\) 条被插入的线段的标号为 \(i\)。
  2. 给定一个数 \(k\)，询问与直线 \(x = k\) 相交的线段中，交点纵坐标最大的线段的编号。

强制在线。

如果用普通线段树实现，大概是要将每个点的函数值算出来，再暴力修改。（还不如直接写暴力？）

于是便有了李超线段树。

概述

李超线段树是运用标记永久化思想的线段树。

它的实现，是记录区间中最优线段。

当我们要记录纵交点最大的线段时：

称一条线段在 \([L,R]\) 最优，满足以下条件：

  1. 线段完整覆盖了 \([L,R]\) 的区间
  2. 线段在区间中点 \(mid\) 处取值最大

插入

具体而言，插入一条新线段 \(l\) 时，设原线段为 \(m\) ，分为如下情况：

  • 线段在 \(L,R\) 处取值均优于原线段 \(\to\) 将区间最优线段更新为 \(l\) 并 return
  • 线段在 \(L,R\) 处取值均不优于原线段 \(\to\) return
  • 线段斜率 \(k_l > k_m\) :
    • 如果 \(l\) 在 \(mid\) 处更优，则它在整个区间必定最优。原线段 \(m\) 在左区间仍可能成为最优线段。
      • 如图：\(l\) 在 \(mid\) 处更优，\(m\) 在左子树可能成为最优（蓝色部分）
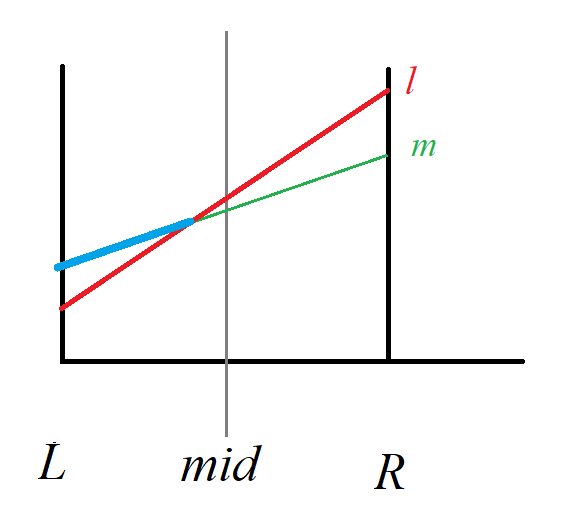
        image
      • 递归左子树判断 \(m\) 成为子区间最优线段。返回后将 \(l\) 设置为区间最优线段。
    • 如果 \(l\) 在 \(mid\) 处不优，则它可能在右区间更优。
      • 如图：\(l\) 在 \(mid\) 处不优，在右子树可能成为最优（蓝色部分）
      • 递归右子树判断 \(l\) 成为子区间最优线段。
  • 线段斜率 \(k_l <k_m\)
    • 如果 \(l\) 在 \(mid\) 处最优，则 \(m\) 在右子区间可能最优。
      • 递归右子树判断 \(m\) 成为子区间最优线段。返回后将 \(l\) 设置为区间最优线段。
    • 如果 \(l\) 在 \(mid\) 处不优，则它可能在左区间更优。
      • 递归左子树判断 \(l\) 成为子区间最优线段。
  • 线段斜率 \(k_l=k_m\) ，此时已经在第一二个判断判断完毕，不需考虑。

查询

查询过程，只需要将所有包含 \(x_0\) 的区间取出来（最多有 \(O(\log n)\) 个），在其中选取最大值即可。

复杂度分析

对于每条新加入的线段，我们需要用 \(\log n\) 的复杂度将它分配到不同的区间内，对于每个区间，又要用 \(\log n\)的复杂度判断在所有子区间的优劣程度。

所以，插入复杂度是 \(\log^2n\) 的，查询复杂度依然为 \(\log n\)。

但是这个操作复杂度是远远达不到这个数量级的。亲测在 \(10^6\) 的数据下跑得飞快。

性质

李超线段树有极好的性质。

  • 每一条线段最多只会被线段树的一个节点记录信息。
    • 这意味着我们可以用动态开点来解决值域极大的情况。
  • 同时，由于使用了标记永久化的思想，使复杂度得以保证。

这里先放上板子题的代码

#include <bits/stdc++.h>
#define fo(a) freopen(a".in","r",stdin), freopen(a".out","a",stdout)
using namespace std;
const int INF = 0x3f3f3f3f, N = 3e5+5, modx = 39989, mody = 1e9;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
	ll ret = 0; char ch = ' ', c = getchar();
	while(!(c >= '0' && c <= '9')) ch = c, c = getchar();
	while(c >= '0' && c <= '9') ret = (ret << 1) + (ret << 3) + c - '0', c = getchar();
	return ch == '-' ? -ret : ret;
}
int n,lans;
int tr[N<<2];
struct Seg{double k,b;}a[N]; int cnt;
inline Seg newseg(double x0,double y0,double x1,double y1){
	if(x0 == x1) return (Seg){0,max(y0,y1)};
	double k = (y1-y0) / (x1-x0), b = y1 - x1*k;
	return (Seg){k,b};
}
inline double f(int w,int x){return a[w].k * x + a[w].b;}
void modify(int k,int l,int r,int x,int y,int w){
	if(l == r) return void(f(w,l) > f(tr[k],l) ? tr[k] = w : 0);
	int mid = (l + r) >> 1;
	if(x <= l && r <= y){
		if(f(w,l) > f(tr[k],l) && f(w,r) > f(tr[k],r)) return void(tr[k] = w);
		if(f(w,l) <= f(tr[k],l) && f(w,r) <= f(tr[k],r)) return;
		if(a[w].k > a[tr[k]].k){
			if(f(w,mid) > f(tr[k],mid))
				modify(k<<1,l,mid,x,y,tr[k]),
				tr[k] = w;
			else modify(k<<1|1,mid+1,r,x,y,w);
		}
		else
			if(f(w,mid) > f(tr[k],mid))
				modify(k<<1|1,mid+1,r,x,y,tr[k]),
				tr[k] = w;
			else modify(k<<1,l,mid,x,y,w);
		return;
	}
	if(x <= mid) modify(k<<1,l,mid,x,y,w);
	if(y > mid)  modify(k<<1|1,mid+1,r,x,y,w);
}
inline int Max(int p,int q,int x){
	return f(p,x) != f(q,x) ? f(p,x) > f(q,x) ? p : q : min(p,q);
}
int query(int k,int l,int r,int x){
	if(l == r) return tr[k];
	int mid = (l + r) >> 1;
	if(x <= mid) return Max(tr[k],query(k<<1,l,mid,x),x);
	else return Max(tr[k],query(k<<1|1,mid+1,r,x),x);
}
signed main(){
	n = read();
	while(n--){
		switch(read()){
			case 0:
				printf("%d\n",lans = query(1,1,modx,(read()+lans-1)%modx+1));
				break;
			case 1:{
				int x0 = (read()+lans-1) % modx + 1, y0 = (read()+lans-1) % mody + 1, x1 = (read()+lans-1) % modx + 1, y1 = (read()+lans-1) % mody + 1;
				if(x0 > x1) swap(x0,x1), swap(y0,y1);
				a[++cnt] = newseg(x0,y0,x1,y1);
				modify(1,1,modx,x0,x1,cnt);
				break;
			}
		}
	}
}

到斜率优化dp

一道例题：

[CEOI2017]Building Bridges

有 \(n\) 根柱子依次排列，每根柱子都有一个高度。第 \(i\) 根柱子的高度为 \(h_i\)。

现在想要建造若干座桥，如果一座桥架在第 \(i\) 根柱子和第 \(j\) 根柱子之间，那么需要 \((h_i-h_j)^2\) 的代价。

在造桥前，所有用不到的柱子都会被拆除，因为他们会干扰造桥进程。第 \(i\) 根柱子被拆除的代价为 \(w_i\)，注意 \(w_i\) 不一定非负，因为可能政府希望拆除某些柱子。

现在政府想要知道，通过桥梁把第 \(1\) 根柱子和第 \(n\) 根柱子连接的最小代价。注意桥梁不能在端点以外的任何地方相交。

\(n\leq 10^5, 0\leq h_i,|w_i|\leq 10^6\)

设 \(s_i=\sum\limits_{k=1}^{i}w_k\)

易得转移方程：

\[dp_i=dp_j+(h_i-h_j)^2+s_{i-1}-s_j \]

将其整理成单调队列维护斜率优化 dp的标准形式：

\[\begin{matrix}dp_i-h_i^2-s_{i-1}&=&dp_j-s_j+h_j^2&-&2h_j\cdot h_i\\b&=&y&-&k\cdot x\end{matrix} \]

其中：

\[\begin{matrix}b&=&dp_i-h_i^2-s_{i-1}\\y&=&dp_j-s_j+h^2_j\\k&=&2h_j\\x&=&h_i \end{matrix} \]

不难发现，这里 \(k\) 不单调，\(x\) 也不单调。

那怎么办？splay维护凸包？

splay实在是细节太多太难写太难调了（至少对我来说）。

我们重新判断这个式子。

它相当于是在平面内加入一条线段，而后令 \(x\) 取不同值时在所有线段中取最小值。

那么我们当然可以用李超线段树来维护啦！

重新写一遍式子

\[\begin{matrix} dp_i-h_i^2-s_{i-1}&=&-2h_j\cdot h_i&+&dp_j+h_j^2-s_j\\ y&=&k\cdot x&+&b \end{matrix} \]

其中

\[\begin{matrix} y&=& dp_i-h_i^2-s_{i-1}\\ k&=& -2h_j\\ x&=&h_i\\ b&=&dp_j+h_j^2-s_j \end{matrix} \]

我们就可以用 \(k,b\) 来描述一条线段，加入到李超线段树里，进行查询了。

注意一点：本题 \(x\) 值域为 \(10^6\) ，但是 \(n=10^5\)，利用动态开点，我们只需要开大小为 \(n\) 的线段树节点就可以了。（甚至不用乘4）

特别注意

李超线段树维护斜率优化时，将直线化成的形式与单调队列/splay大不相同。

  • 单调队列/splay ： \(b=y-kx\)

  • 李超线段树： \(y=kx+b\)

使用时不能混淆。必须确定使用的是哪种表达式。

例题代码：

#include <bits/stdc++.h>
#define fo(a) freopen(a".in","r",stdin), freopen(a".out","a",stdout)
using namespace std;
const int INF = 0x3f3f3f3f, N = 1e5+5;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
	ll ret = 0; char ch = ' ', c = getchar();
	while(!(c >= '0' && c <= '9')) ch = c, c = getchar();
	while(c >= '0' && c <= '9') ret = (ret << 1) + (ret << 3) + c - '0', c = getchar();
	return ch == '-' ? -ret : ret;
}
int n, m;
ll h[N],s[N];
ll dp[N];
struct Seg{ll k,b;}a[N];
struct Segtre{int ls,rs,w;}tr[N<<2];
int tot,rt;
inline ll f(int p,int x){return a[p].k * x + a[p].b;}
void modify(int &k,int l,int r,int w){
	if(!k)
		return void(tr[k = ++tot].w = w);
	if(l == r)
		return void(f(w,l) < f(tr[k].w,l) ? tr[k].w = w : 0);
	if(f(w,l) < f(tr[k].w,l) && f(w,r) < f(tr[k].w,r))
		return void (tr[k].w = w);
	if(f(w,l) >= f(tr[k].w,l) && f(w,r) >= f(tr[k].w,r))
		return;
	int mid = (l + r) >> 1;
	if(a[w].k < a[tr[k].w].k){
		if(f(w,mid) < f(tr[k].w,mid))
			modify(tr[k].ls,l,mid,tr[k].w),
			tr[k].w = w;
		else modify(tr[k].rs,mid+1,r,w);
	}
	else{
		if(f(w,mid) < f(tr[k].w,mid))
			modify(tr[k].rs,mid+1,r,tr[k].w),
			tr[k].w = w;
		else modify(tr[k].ls,l,mid,w);
	}
}
ll query(int k,int l,int r,int x){
	if(!k) return 1ll * INF * INF;
	if(l == r) return f(tr[k].w,x);
	int mid = (l + r) >> 1;
	return min(f(tr[k].w,x),x <= mid ? query(tr[k].ls,l,mid,x) : query(tr[k].rs,mid+1,r,x));
}
signed main(){
	n = read(); 
	for(int i = 1 ; i <= n ; i ++) m = max(1ll*m,h[i] = read());
	for(int i = 1 ; i <= n ; i ++) s[i] = s[i-1] + read();
	
	a[0] = (Seg){0,1ll*INF*INF};
	a[1] = (Seg){-2*h[1],dp[1] + h[1]*h[1] - s[1]};
	for(int i = 2 ; i <= n ; i ++){
		a[i-1] = (Seg){-2*h[i-1],dp[i-1] + h[i-1]*h[i-1] - s[i-1]};
		modify(rt,0,m,i-1);
		dp[i] = query(rt,0,m,h[i]) + h[i] * h[i] + s[i-1];
	}
	printf("%lld",dp[n]);
}
posted @ 2021-11-16 10:49  Last-Order  阅读(815)  评论(1)  编辑  收藏  举报