机器学习模型（二）决策树

导语：局部空间的线性拟合非线性（近邻分析，决策树），高维空间平面在低维空间的展示（例如：多项式；神经网络；SVM用核函数假装去高维）。

二、决策树（规则集）if-then

目前以二叉树为主，多叉树逐渐没落。更适合输入变量中分类变量很多的情况。

变量重要性是从区分角度定义。

（一）图形表示

• 分组过程是对p维空间不断划分的过程，每一刀都平行或垂直另外的轴
• 怎么决定第一刀横着切还是竖着切：分出来的组内异质性最小，即信息增益最大
• 回归：区域的平均值视为预测值

（二）CART算法（分类回归树算法）

• 区间划分的策略，贪心算法不断迭代。确定当前最优的策略
• 异质性的度量
  • 1. 切前后的方差的差距大（回归）
  • 2. 基尼系数（分类）：越高，异质性越强

                     

• 3. 熵（C4.5）：从完全不确定到完全确定信息的价值

                     

• • 若这个信息消除了大部分不确定性，有价值
  • 熵越小没有不确定性
• 使用中，基尼系数与熵没有太大的差异性

 （三）剪枝

• 避免决策树过拟合：预修剪（限制树深度；子节点样本数），后修剪（Python默认不做，最小代价复杂度剪枝）
• 代价复杂度=训练误差（对于回归，误差平方和；对于分类，总的错判率）+CP参数（越小，选择更复杂的树；越大，选择更简单的树。Python的默认参数为0）*树的复杂度（叶节点的个数）

          

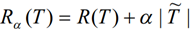
• • 中间节点的代价复杂度VS子节点的代价复杂度，选代价复杂度更小的那棵树
  • 若训练误差与树的复杂度的组合，两棵树的代价复杂度相等，选更简单的那一个
• 剪枝原理上类似回归中的AIC，负的似然函数