学习笔记——组合计数

前言

本章和数学关系较深，深刻理解组合数便可以在本章学的游刃有余。

加法原理

做一件事情，完成它有\(n\)类方式，第一类方式有\(a_1\)种方法，第二类方式有\(a_2\)种方法，……，第\(n\)类方式有\(a_n\)种方法，那么完成这件事情共有\(a_1+a_2+...+a_n\)种方法。——百度百科

乘法原理

做一件事，完成它需要分成\(n\)个步骤，做第一步有\(a_1\)种不同的方法，做第二步有\(a_2\)种不同的方法，……，做第\(n\)步有\(a_n\)种不同的方法。那么完成这件事共有\(a_1 \times a_2 \times ... \times a_n\)种不同的方法。——百度百科

用图片来解释，就是

加法原理（从\(1\)到\(10\)的方法总数）

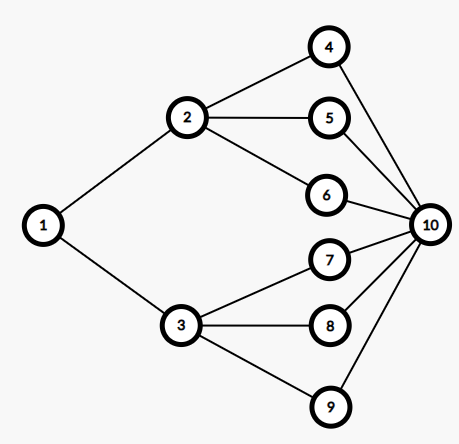
乘法原理（从\(1\)到\(7\)的方法总数）

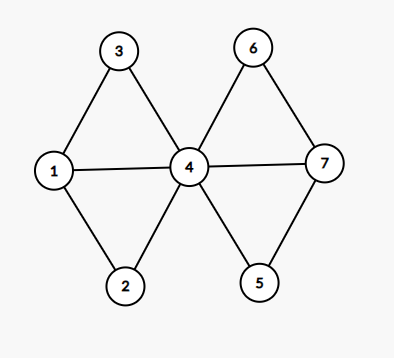
排列数

排列数指的是从\(n\)个不同元素中任取\(m(m \le n)\)个元素排成一列（考虑元素先后出现次序）称此为一个排列，此种排列的总数即为排列数，即叫做从\(n\)个不同元素中取出\(m\)个元素的排列数。——百度百科

\[A_n^m = \frac{n!}{(n-m)!}= n \times (n-1) \times ... \times (n-m+1) \]

组合数

从\(n\)个不同元素中，任取\(m(m \le n)\)个元素并成一组，叫做从\(n\)个不同元素中取出\(m\)个元素的一个组合，从\(n\)个不同元素中取出\(m(m \le n)\)个元素的所有组合的个数，叫做从\(n\)个不同元素中取出\(m\)个元素的组合数。——百度百科

\[C_n^m = \frac{n!}{m!(n-m)!}= n \times \frac{(n-1) \times ... \times (n-m+1)}{m \times (m-1) \times ... \times 1} \]

性质

• \(1.c_n^m = c_n^{n-m}\)

• \(2.c_n^m = c_{n-1}^m + c_{n-1}^{m-1}\)

• \(3. c_n^0 + c_n^1 + ... + c_n^n = 2^n\)

证明：

\(1.\)对于从\(n\)个元素中取出\(m\)个组成每个集合，剩下的\(n-m\)个元素也组成了一个集合，所以方案数相同。

\(2.\)对于从\(n\)个元素中取出\(m\)个组成每个集合的方案总数，可以从\(n-1\)个元素中选\(m\)个（不选当前元素），也可以从\(n-1\)个元素中选\(m-1\)个再加上当前元素（选当前元素）。

\(3.\)从\(n\)个元素中取出若干个元素组成集合，有\(n+1\)类方法，分别是取出\(0,1,...,n\)个元素，即\(c_n^0 + c_n^1 + ... + c_n^n\)。又因为含\(n\)个元素的集合的子集有\(2^n\)，两者数量上相等。

组合数的求法

组合数的结果一般比较大，所以题目一般会给出模数\(p\)。

• \(1\).新开两个数组\(jc[N],jc_{inv}[N]\)，分别记录\(i\)的阶乘模\(p\)后的值及\(i\)的阶乘模\(p\)意义下的逆元，预处理时间复杂度\(O(n )\)，之后依

\[C_n^m \equiv jc[n] \times jc_{inv}[n-m] \times jc_{inv}[m] \pmod{p} \]

• \(O(1)\)回答组合数\(C_n^m\)的值。

	jc[0]=1;
	for(re int i=1;i<=n;++i) jc[i]=jc[i-1]*i%MOD;
	jc_inv[n]=ksm(jc[n],MOD-2,MOD);
	for(re int i=n;i;--i) jc_inv[i-1]=jc_inv[i]*i%MOD;

• \(2\).依组合数的性质二预先处理出所有组合数，时间复杂度\(O(n^2)\)

P2822 [NOIP2016 提高组] 组合数问题（题解）（我的代码）

二项式定理

\[(a+b)^n = \sum_{i=0}^nC_n^ia^ib^{n-i} \]

证明：

• 当\(n=1\)时，\((a+b)^1 = C_1^0a^0b^1 + C_1^1a^1b^0 =a+b\)，成立

• 当\(n \ge 1\)时，令\(n=m+1\)

\[(a+b)^{m+1} =(a+b)(a+b)^m =(a+b) \sum_{i=0}^mC_m^ia^ib^{m-i} \]

\[= \sum_{i=0}^mC_m^ia^{i+1}b^{m-i} + \sum_{i=0}^mC_m^ia^ib^{m-i+1} \]

\[= \sum_{i=1}^{m+1}C_m^{i-1}a^{i}b^{m-i+1} + \sum_{i=0}^mC_m^ia^ib^{m-i+1} \]

\[= \sum_{i=0}^{m+1}(C_m^{i-1}+ C_m^i)a^ib^{m-i+1} \]

\[= \sum_{i=0}^{m+1}C_{m+1}^{i}a^ib^{m-i+1} \]

211. 计算系数（题解）（我的代码）

多重集的排列数

多重集是指包含重复的广义集合。设\(S= \{ n_1 \centerdot a_1, n_2 \centerdot a_2,...,n_k \centerdot a_k \}\)是由\(n_1\)个\(a_1\)，\(n_2\)个\(a_2\)...\(n_k\)个\(a_k\)组成的多重集，记\(n=n_1+n_2+...+n_k\)，\(S\)的全排列个数为

\[\dfrac{n!}{n_1!n_2!...n_k!} \]

理解：

\(n!\)是所有数的全排列个数，\(n_k!\)是\(n_k\)个相同的数的全排列个数，用所有数的全排列个数除去相同的数的全排列个数即为多重集\(S\)的全排列个数。

多重集的组合数

设\(S= \{ n_1 \centerdot a_1, n_2 \centerdot a_2,...,n_k \centerdot a_k \}\)是由\(n_1\)个\(a_1\)，\(n_2\)个\(a_2\)...\(n_k\)个\(a_k\)组成的多重集，设整数\(r \le n_i(\forall i \in [1,k])\)。从\(S\)中取出\(r\)个元素组成一个多重集（不考虑元素的顺序），产生的不同多重集的数量为

\[C_{k+r-1}^{k-1} \]

证明：

原问题等价于统计下列集合的数量：\(\{ x_1 \centerdot a_1, x_2 \centerdot a_2,...,x_k \centerdot a_k \}\)，其中\(\sum_{i=1}^kx_i=r\)并且\(x_i \le n_i\)。因为\(r \le n_i\)，必有\(x_i \le n_i\)，所以只用考虑\(\sum_{i=1}^kx_i=r\)。

故原问题等价于\(r\)个\(0\)，\(k-1\)个\(1\)构成的全排列数——\(k-1\)个\(1\)把\(r\)个\(0\)分成\(k\)组，每一组\(0\)的数量对应\(x_i\)。而多重集${ r \centerdot 0, (k-1) \centerdot 1 $} 的全排列数为

\[\frac{(r+k-1)!}{r!(k-1)!}=C_{k+r-1}^r=C_{k+r-1}^{k-1} \]

212. 计数交换（题解）（我的代码）

\(Lucas\)定理

若\(p\)是质数，则对于任意整数\(1 \le m \le n\)，有：

\[C_n^m \equiv C_{n \mod{p}}^{m \mod{p}} \times C_{n/p}^{m/p} \pmod{p} \]

P3807 【模板】卢卡斯定理/Lucas 定理（证明）（题解代码）（我的代码）

P2480 [SDOI2010]古代猪文（题解）（我的代码）

\(prufer\)序列

转化1：无根树->\(prufer\)序列

• 找到一个度数为\(1\)，且编号最小的点。（其中编号最小保证了后面将会提到的\(prufer\)序列的唯一对应性，同时也方便从\(prufer\)序列转化回无根树）

• 将该节点的父节点加入序列，删除该节点

重复以上操作直到树只剩下两个节点，得到的长度为\(n-2\)的序列即为\(prufer\)序列。

转化2：无根树->\(prufer\)序列

• 取出\(prufer\)序列最前面的元素\(x\)。

• 取出在点集中的、且当前不在\(prufer\)序列中的最小元素\(y\)。（这恰好呼应了前面提到过的选取编号最小的节点）

• 在\(x,y\)之间连接一条边。（注意前面的取出相当于删除）

重复以上操作直到点集中只剩下两个点，剩下的两个点连边。

\(prufer\)序列的性质

• \(prufer\)序列与原无根树一一对应。

根据上述转化的唯一性可知成立。

• 度数为\(d[i]\)的节点会在\(prufer\)序列中出现\(d[i]-1\)次。

由无根树转\(prufer\)序列的操作可知，度数为\(1\)的节点会被直接删去，度数不为\(1\)的节点每删去一个与之相邻的节点都会加入序列一次，一共\(d[i]-1\)次

• 一个\(n\)个节点的完全图的生成树有\(n^{n-2}\)种

\(prufer\)序列有\(n-2\)个数，每个位置上有\(n\)种可能的情况（\(n\)个节点），又根据性质一，得证

• 对于给定度数为\(d_{1 \sim n}\)的一根无根树，一共有\(\frac{(n-2)!}{\prod_{i=1}^n{(d_i-1)!}}\)种情况

由上述性质可知，度数为\(d[i]\)的节点会在\(prufer\)序列中出现\(d[i]-1\)次，用总的全排列数除以重复的元素的全排列数即可得到给定度数的可重全排列集。

P2290 [HNOI2004]树的计数（prufer序列介绍）（题解）（我的代码）

P4921 [MtOI2018]情侣？给我烧了！（题解）（我的代码）

P4931 [MtOI2018]情侣？给我烧了！（加强版）（我的代码）

设\(g[k]\)为\(k\)对情侣全部错开的方案数，则答案可表示为

\[ans_k=C_n^k \times A_n^k \times 2^k \times g[n-k] \]

• \(C_n^k\)表示从\(n\)对座位中无序的选出\(k\)对给情侣坐。

• \(A_n^k\)表示从\(n\)对情侣中有序（情侣顺序不同表示不同的方案）选出\(k\)对情侣。

• \(2^k\)表示选出的\(k\)对情侣可以左右互换位置（男女、女男）的方案数

• \(g[n-k]\)表示有\(n-k\)对情侣错开，即剩下的\(k\)对情侣坐在一起。

之后我们来求\(g[k]\)的递推式，

当一排的人不配对

• 1.两个男的或两个女的。我们从\(k\)对情侣中无序地选出两个，因为两个人的顺序可以交换，所以方案数为\(2\)（选出的两个人的顺序可以交换）\(\times C_k^2\)（\(k\)个人中随机选两个）\(=2 \times k \times (k-1)\)

• 2.一男一女但不是情侣。我们从\(k\)个男的里面随机选一个，因为要满足不是情侣，所以只能从\(k-1\)个女的中选一个，同样可以交换顺序，所以方案数为\(2 \times k \times (k-1)\)

综上，当一排的人不配对时方案数有\(4 \times k \times (k-1)\)种。

再考虑这排人原本对应的情侣

• 1.两人对应的情侣坐在同一排。情侣可以在剩下的\(k-1\)排中随便找一排且这两人可以左右换顺序，可由\(g[k-2]\)推来，即\(g[k]+=4 \times k \times (k-1)\)（一排人不配对的方案数） \(\times 2 \times (k-1)\)（两人对应的情侣坐在同一排的方案数）$ \times g[k-2]$

• 2.两人对应的情侣不坐在同一排。可由\(g[k-1]\)推来，即\(g[k]+=4 \times k \times (k-1)\)（一排人不配对的方案数） \(\times g[k-1]\)

最终，我们整理得：

\[g[k]=4 \times k \times (k-1) \times (g[i-1]+2 \times (k-1) \times g[i-2]) \]

P5377 [THUPC2019]鸽鸽的分割（题解）（我的代码——公式解法）（我的代码——组合数解法）

解法一：组合数（正经解法）

根据欧拉公式，我们知道\(R + V - E = 2\)，其中\(R\)表示区域个数，\(V\)表示节点个数，\(E\)表示边的个数。

通过移项，我们可以得到\(R = E - V + 2\)。

对于\(V\)：

• 圆上有\(n\)个节点

• 每两条线都有一个交点，一共有\(C_n^4\)个交点

对于\(E\)：

• 圆上\(n\)个节点将圆分成\(n\)个弧

• 每两个节点有一条连线，一共有\(C_n^2\)条连线

• 每两条连线的交点将这两条连线分成四个部分，即比原来多两条连线，即\(2 \times C_n^4\)

所以\(ans=2 + C_n^2+ 2 \times C_n^4 + n - C_n^4 -n =C_n^2 + C_n^4 + 2\)

又因为是在圆内，不是在平面上，所以要减少一个区域，即\(ans=C_n^2 + C_n^4 + 1\)

解法二：暴力解方程（洋葱数学\(yyds\)）

列出前\(6\)项，可以暴力解\(an^5+bn^4+cn^3+dn^2+en+f\)中的\(a,b,c,d,e,f\)，可以求出其通项为

\[(n^4-6 \times n^3 + 23 \times n^2 - 18 \times n + 24)/24 \]

解法三：（逃课解法）

先手动求出该数列的前\(6\)项分别为\(1,2,4,8,16,31,57\)，输入OEIS中找通项即可

P4981 父子（题解）（我的代码）

题意简述：给定\(n\)个节点，求有多少种不同的有根树。

根据\(prufer\)序列的性质，我们知道\(n\)个节点构成的无根树有\(n^{n-2}\)种，这些无根树的每一个节点都可以当做根节点，所以一共有\(n^{n-1}\)种不同的有根树。

卡特兰数

给定\(n\)个元素进出栈，则其合法出栈序列总数为：

\[Cat_n=\frac{C_{2n}^n}{n+1} \]

证明：

我们将进栈记为\(+1\)，出栈记为\(-1\)，

\(n\)个\(-1\)和\(n\)个\(1\)，它们按照某种顺序排成长度为\(2n\)的序列，一共有\(C_{2n}^n\)种排列方法

对于一个不合法的序列，它一定有一项前缀和小于\(0\)，我们将第一个前缀和小于\(0\)的所有元素取反（加个负号），那我们就得到了由\(n+1\)个\(1\)和\(n-1\)个\(-1\)组成的序列，该序列一共有\(C_{2n}^{n+1}\)种排列方式。（因为取反序列与不合法序列一一对应，所以不合法序列的排列方式也是\(C_{2n}^{n+1}\)种）

用总的排列方式减去不合格的排列方式，即可得到\(Cat_n=C_{2n}^n-C_{2n}^{n+1}=\frac{2n!}{n!(n+1)!}=\frac{C_{2n}^n}{n+1}\)

卡特兰数的递推式

\[Cat_n=\sum_{i=0}^{n-1} Cat_{i} \times Cat_{n-i-1} =Cat_{n-1} \times \frac{4\times n-2}{n+1}=\frac{C_{2n}^n}{n+1}=C_{2n}^n-C_{2n}^{n+1} \]

一般来说，最后一种递推式最好（第一种要\(O(n^2)\)的时间，第二、三种要执行取模意义下的除法，并且第四种最普遍）

卡特兰数可解决的问题

1.\(n\)个元素进出栈，合法的进出栈序列数量为\(Cat_n\)

2.\(n\)个左括号和\(n\)个右括号组成的合法括号序列的数量为\(Cat_n\)（左括号看成\(+1\)，右括号看成\(-1\)，之后同\(1\)）

3.\(n\)个节点构成的不同二叉树的数量为\(Cat_n\)。

我们可以枚举根节点的左子树节点个数，左子树节点数可以有\(0 \sim n-1\)（因为根节点也是一个节点，所以左子树最多到\(n-1\)），则

\[f[n]=\sum_{i=0}^{n-1} f[i] \times f[n-i-1] \]

就是卡特兰数列

4.\(n+1\)个叶子节点能构成\(Cat_n\)棵不同的国际满二叉树（国际满二叉树：一个节点要么是叶子节点，要么有两个子节点）

我们可以从根节点开始对国际满二叉树进行深搜，向左子树走记为\(+1\)，右子树走记为\(-1\)，则同1可得。（每个非叶节点都会有一次\(+1\)一次\(-1\)，\(n+1\)个叶节点的国际满二叉树有\(n\)个非叶节点）

5.在平面直角坐标系上，每一步只能向上或向右走，从\((0,0)\)走到\((n,n)\)并且除两个端点外不接触直线\(y=x\)的路线数量为\(Cat_{n}\)

我们同样将向右走视为\(+1\)，向上走视为\(-1\)，要时刻保持向右走的步数大于向上走的步数，即前缀和始终大于\(0\)，由\(1\)得证

6.圆周上有标号为\(1,2,3,...2n\)的共计\(2n\)个点，这\(2n\)个点配对可连成\(n\)条弦，且这些弦两两不相交的方式数为卡特兰数\(Cat_n\)。

由于弦两两不相交，所以每一根弦都将圆分成两部分，每部分可以有\(0 \sim n-1\)条弦，即

\[f[n]=\sum_{i=0}^{n-1} f[i] \times f[n-i-1] \]

就是卡特兰数列

7.公园门票一张一元，售票处没有零钱，有\(n\)个只有一元、\(m\)个只有两元的游客，游客都进入公园的合法排列方式有\((Cat_{n+m}^n-Cat_{n+m}^{n+1}) \times n! \times m!\)

同样将\(n\)名游客看成\(+1\)，\(m\)名游客看成\(-1\)，这些游客一共有\(C_{n+m}^n\)种排列方式，同样对于一个不合法的序列，它一定有一项前缀和小于\(0\)，我们将第一个前缀和小于\(0\)的所有元素取反（加个负号），那我们就得到了由\(n+1\)个\(1\)和\(m-1\)个\(-1\)组成的序列，该序列一共有\(C_{n+m}^{n+1}\)种排列方式。（因为取反序列与不合法序列一一对应，所以不合法序列的排列方式也是\(C_{n+m}^{n+1}\)种）

例题

P1044 [NOIP2003 普及组] 栈（基础板子）（题解）（我的代码）

P1976 鸡蛋饼（基础板子）（题解）（我的代码）

P1754 球迷购票问题（基础板子）（题解）（我的代码）

P2532 [AHOI2012]树屋阶梯（题解）（题解）（我的代码）

我们可以枚举每一个拐点，拐点将台阶分为\(0 \sim n-1\)两部分，即

\[f[n]=\sum_{i=0}^{n-1} f[i] \times f[n-i-1] \]

就是卡特兰数列。

P3200 [HNOI2009]有趣的数列（题解）（题解）（我的代码）

本题要求数列的偶数位比前一个偶数位大，又要比其对应的奇数位大，即对于任意的偶数位，其数值大于前面所有位的数值，那么偶数位上的数最小就是其下标，每次放的数必须放在最前的奇数/偶数位上，即数列填入偶数位的个数要时刻不超过填入奇数位的个数（如果偶数位的个数超过填入奇数位的个数，那后一位的奇数位就无法放入合法的数了），这样就可以用卡特兰数处理。

P3978 [TJOI2015]概率论（题解）（我的代码）

• 对于每个\(n\)个节点的有根二叉树，假设其有\(k\)个叶子节点，分别将这\(k\)个叶子结点删去，可以得到\(k\)棵\(n-1\)节点的二叉树

• 每颗\(n-1\)节点的二叉树恰好有\(n\)个位置可以加入一个新叶子节点，所以每个\(n-1\)节点的二叉树可以得到\(n\)棵新树

• 所以\(n\)个节点的二叉树叶子数和等于\(n-1\)节点的二叉树个数\(\times n\)

由性质\(3\)知，\(n\)个节点构成的不同二叉树的数量为\(Cat_n\)。

P1641 [SCOI2010]生成字符串（题解）（题解）（我的代码）

本题为性质\(5\)的推论，我们可以把\(1\)看成在网格上向右走，\(0\)看成在网格上向上走，同样不能越过\(y=x\)直线，一共有\(C_{n+m}^n\)中方法走到终点\((n,m)\)，对第一次越过直线\(y=x\)的前面所有操作进行取反，将会有\(n+1\)次向右走，\(m-1\)次向上走的不合法序列，所以答案为\(C_{n+m}^n-C_{n+m}^{n+1}\)

SP19148 INS14G - Kill them All（题解）（我的代码）

本题是上题的加强版，要求严格大于（即不能接触直线\(y=x\)），从\((1,0)\)开始走\(n-1\)步，就是上一题的不合法序列数，即
\(\binom{n-1}{\left\lceil\dfrac{n}{2}\right\rceil-1}\)

P4769 [NOI2018] 冒泡排序（题解）（我的代码）

本题加上了字典序的限制，我们可以统计每一位的限制，对应的网格图上只走限制点的右下部分，最后统计方案数即可。

参考资料

《算法竞赛进阶指南》

「算法入门笔记」卡特兰数