学习笔记—— *衡树
一、前言
总所周知,数论和树论是\(OI\)界的两大毒瘤,而今天,我们也将推开 (入土) *衡树的大门,感受其特有的魅力(duliu)。
二、*衡树的一些概念
1.二叉查找树(BST)
给定一颗二叉树,树上的每个节点带有一个数值,称为节点的“关键码”。
它有以下性质:
-
该节点的关键码不小于它左子树中任何节点的关键码。
-
该节点的关键码不大于它右子树中任意节点的关键码。
满足上述性质的二叉树就是一颗“二叉查找树(BST)”,且它的中序遍历是一个关键码非严格单调递增的节点序列。
BST的建立
一般来说,我们为了避免越界,减少边界情况的特殊判断,可以在\(BST\)中插入两个额外的关键码分别为\(INF\)和\(-INF\)的节点,并用\(cnt\)记录和当前节点关键码相同的节点数。
上代码
int val[N],cnt[N];
//val[i]表示i节点的关键码
//cnt[i]表示i节点的副本数(与它相同关键码的节点数)
int ch[N][2];
//ch[i][0]表示i节点的左儿子的编号
//ch[i][1]表示i节点的右儿子的编号
il int NEW(int v){
val[++tot]=v;//当前节点的关键码
cnt[tot]=1;//因为是新节点,所以副本数为1
return tot;//tot表示该节点的编号
}
il void build() {
root=NEW(-INF);ch[root][1]=NEW(INF);
//先建两个节点,避免越界
//因为INF>-INF,所以INF是-INF的右儿子
}
BST的检索
由\(BST\)的性质,我们可以在\(O(logn)\)的复杂度内找到关键码为\(val\)的节点,过程如下(设\(id\)为当前节点的编号):
-
1.若\(id\)的关键码等于\(val\),直接返回\(id\)
-
2.若\(id\)的关键码大于\(val\)
(1)若\(id\)的左儿子为空,则没有关键码为\(val\)的节点
(2)若\(id\)的左儿子不为空,则在\(id\)的左子树中查找
-
3.若\(id\)的关键码小于\(val\)
(1)若\(id\)的右儿子为空,则没有关键码为\(val\)的节点
(2)若\(id\)的右儿子不为空,则在\(id\)的右子树中查找
\(Talk\) \(is\) \(cheap\) ,\(show\) \(you\) \(the\) \(code\)
il int get_rank(int id,int v) {
if(!id) return 0;//没找到
if(v==val[id]) return id;//情况1
else if(v<val[id]) return get_rank(ch[id][0],v);//情况2
else return get_rank(ch[id][1],v);//情况3
}
BST的插入
和检索一样,当我们搜索到\(id\)的子节点为空时,直接建立关键码为\(val\)的新节点作为\(id\)的子节点。当搜索到时,直接令\(id\)节点的副本数\(+1\)。
\(Talk\) \(is\) \(cheap\) ,\(show\) \(you\) \(the\) \(code\)
il void insert(int &id,int v) {//注意,此时id为取地址符号,可以使id节点的父节点的ch[fa[id]][d]更新
if(!id) {
id=NEW(v);//建立一个新节点
return ;
}
if(v==val[id]) ++cnt[id];//直接加副本数
else {
int d=v<val[id]?0:1;//判断方向
insert(ch[id][d],v);
}
}
BST求前驱/后继
定义:
前驱:在\(BST\)中关键码小于\(val\)的前提下,关键码最大的节点。
后继:在\(BST\)中关键码大于\(val\)的前提下,关键码最小的节点。
过程:
之前和检索一样,对于找到该值后的情况,我们可以分类讨论
求前驱时,可以走到该节点的左节点,再一直往右走,就可以找到\(val\)的前驱。
求后继时,可以走到该节点的右节点,再一直往左走,就可以找到\(val\)的后继。
\(Talk\) \(is\) \(cheap\) ,\(show\) \(you\) \(the\) \(code\)
il int get_pre(int v) {
int id=root,pre;
while(id) {
if(val[id]<v) pre=val[id],id=ch[id][1];
//因为val[id]小于v,且val[id]一定不断变大,所以不用取max
else id=ch[id][0];
//当val[id]==v时,id会往左子树上走,然后一直向右,最后找到的pre就是v的前驱
//当val[id]>v时,要一直往左走才能找到v的前驱
}
return pre;
}
il int get_next(int v) {
int id=root,nxt;
while(id) {
if(val[id]>v) nxt=val[id],id=ch[id][0];
else id=ch[id][1];
}
//原理同上,就不再解释了
return nxt;
}
BST的节点删除
先在\(BST\)中检索\(val\),得到其节点\(id\);
-
若\(id\)节点的副本数大于\(1\)(\(cnt[id]>1\)),直接删除其一个副本即可。
-
若\(id\)节点的子树数小于\(2\),直接令其子节点代替\(id\)节点的位置。
-
若\(id\)节点有两颗子树,则先求出\(val\)的后继节点\(nxt\),删除\(nxt\)并用\(nxt\)的右子树代替\(nxt\)的位置,再用\(nxt\)节点代替\(id\)节点位置并删除\(id\)节点即可。
\(Talk\) \(is\) \(cheap\) ,\(show\) \(you\) \(the\) \(code\)
il void Remove(int &id,int v) {//从以id为根的子树中删除值为v的节点
if(!id) return ;//没有该节点,直接返回
if(v==val[id]) {//检索到该节点
if(cnt[id]>1) {--cnt[id];return ;}//副本数大于1,直接减副本数
if(ch[id][0]==0) id=ch[id][1];//没有左儿子,直接用右子树代替id的位置
else if(ch[id][1]==0) id=ch[id][0];//没有右儿子,直接用左子树代替id的位置
else {
int nxt=ch[id][1];
while(ch[id][0]) nxt=ch[id][0];
//因为已经检索到了该节点,所以只要从它的右子树一直往左走即可找到其后继
Remove(ch[id][1],val[nxt]);//删除后继节点
ch[nxt][0]=ch[id][0];
ch[nxt][1]=ch[id][1];
id=nxt;
//用后继节点代替当前节点
}
}
if(v<val[id]) Remove(ch[id][0],v);//往左子树上检索val
else Remove(ch[id][1],v);//往右子树上检索val
}
由上述操作可以看出,\(BST\)在随机数据中一次操作的期望时间复杂度为\(O(logn)\)。但如果其变成一条链,则一次操作的期望时间复杂度会退化为\(O(n)\)。我们追根溯源,可以发现这是由于其左右子树大小相差较大造成的不*衡,而维持其*衡的方法有很多,从而产生了各种*衡树。
三、几种*衡树 (终于讲到*衡树了)
一、有旋\(Treap\)
因为满足\(BST\)性质且中序遍历为相同序列的二叉查找树是不唯一的,但又都是等价的,所以我们可以在维持\(BST\)性质的基础上,改变二叉查找树的形态,使树上每个节点的左右子树大小达到*衡,从而使整颗树的深度维持在\(O(logn)\)级别。(不一定是完全二叉树,但尽量*衡)
改变形态并保持\(BST\)性质的方法就是“旋转”,包括左旋和右旋,如下图:
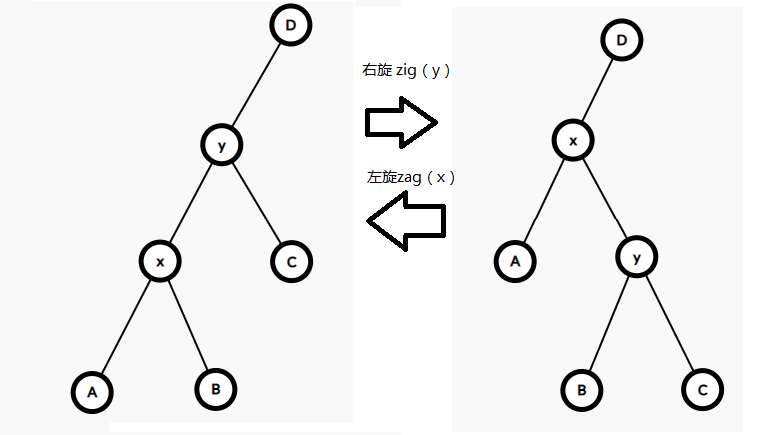
\(Talk\) \(is\) \(cheap\) ,\(show\) \(you\) \(the\) \(code\)
il void Rotate(int &id,int d) {//d=0时为左旋,1时为右旋
int temp=ch[id][d^1];
ch[id][d^1]=ch[temp][d];
ch[temp][d]=id;
id=temp;
}
理解参照上图,这里讲一下记忆技巧(\(from\) 天上一颗蛋 大佬)
在旋转操作中,每一个数据都是被记录后立马修改的,所以会形成“\(Z\)”型,即每一行的末尾变量就是下一行的开头变量。
知道了维持*衡的操作,我们怎样判断该节点是否应该旋转呢?
由对\(BST\)的分析,我们知道,在随机数据的情况下\(BST\)差不多就是*衡的,所以我们可以给每一个节点额外增加一个随机权值,使整颗二叉查找树满足堆的性质。这样,这颗二叉查找树就同时满足了“\(Tree\)”和“Heap”的性质,合在一起就是我们的\(Treap\)算法了。
具体一点,就是当我们插入一个节点时,自底而上依次检查,对于不满足堆性质的节点进行旋转。删除一个节点时,找到需要删除的节点并把它向下旋转成叶子节点,最后直接删除(可避免节点信息更新、堆性质维护等复杂问题)。
\(Talk\) \(is\) \(cheap\) ,\(show\) \(you\) \(the\) \(code\)
const int N=1e5+10,INF=1e18;
int n,tot,root;
int val[N],dat[N],siz[N],cnt[N];
//val[i]表示i节点的关键码
//dat[i]表示随机出的i节点的优先度
//siz[i]表示以i节点为根节点的子树大小
//cnt[i]表示i节点的副本数
int ch[N][2];
//ch[i][0]表示i节点的左儿子的编号
//ch[i][1]表示i节点的右儿子的编号
il int NEW(int v){//建立新节点
val[++tot]=v;
dat[tot]=rand();//赋值随机优先度
siz[tot]=1;
cnt[tot]=1;
return tot;//返回新节点的编号
}
il void pushup(int id) {//更新以id节点为根的子树的大小
siz[id]=siz[ch[id][0]]+siz[ch[id][1]]+cnt[id];
}
il void build() {//建树
root=NEW(-INF);ch[root][1]=NEW(INF);/
//初始时建立INF和-INF两个节点,防止越界
pushup(root);
}
il void Rotate(int &id,int d) {//旋转(包括左旋和右旋)
//d=0表示左旋,1表示右旋,理解参照上图
int temp=ch[id][d^1];
ch[id][d^1]=ch[temp][d];
ch[temp][d]=id;
id=temp;
pushup(ch[id][d]);pushup(id);
}
il void insert(int &id,int v) {//插入节点
if(!id) {//原先没有,就新建一个节点插入
id=NEW(v);
return ;
}
if(v==val[id]) ++cnt[id];//原先有,就在该节点处新加一个副本
else {
int d=v<val[id]?0:1;//判断插入左子树还是右子树
insert(ch[id][d],v);
if(dat[id]<dat[ch[id][d]]) Rotate(id,d^1);//自底而上维护优先度呈堆的性质
}
pushup(id);//更新
}
il void Remove(int &id,int v) {//删除节点
if(!id) return ;//没有该节点,不删除
if(v==val[id]) {//找到该节点
if(cnt[id]>1) {--cnt[id];pushup(id);return ;}//删副本
if(ch[id][0]||ch[id][1]) {
if(!ch[id][1]||dat[ch[id][0]]>dat[ch[id][1]]) {Rotate(id,1);Remove(ch[id][1],v);}//将该节点旋转到叶子节点
else {Rotate(id,0);Remove(ch[id][0],v);}//将该节点旋转到叶子节点
pushup(id);//更新
}
else id=0;//没有子树,直接删
return ;
}
v<val[id]?Remove(ch[id][0],v):Remove(ch[id][1],v);//检索该节点的位置
pushup(id);//更新
}
il int get_rank(int id,int v) {
if(!id) return 0;
if(v==val[id]) return siz[ch[id][0]]+1;
else if(v<val[id]) return get_rank(ch[id][0],v);
else return siz[ch[id][0]]+cnt[id]+get_rank(ch[id][1],v);
}
il int get_val(int id,int rank) {
if(!id) return INF;//没找到
if(rank<=siz[ch[id][0]]) get_val(ch[id][0],rank);//在左子树中找
else if(rank<=siz[ch[id][0]]+cnt[id]) return val[id];//就是该节点的值
else return get_val(ch[id][1],rank-siz[ch[id][0]]-cnt[id]);
//在右子树中查找,其在右子树中的排名要减去左子树大小及当前节点副本数
}
il int get_pre(int v) {
int id=root,pre;
while(id) {
if(val[id]<v) pre=val[id],id=ch[id][1];
//因为val[id]小于v,且val[id]一定不断变大,所以不用取max
else id=ch[id][0];
//当val[id]==v时,id会往左子树上走,然后一直向右,最后找到的pre就是v的前驱
//当val[id]>v时,要一直往左走才能找到v的前驱
}
return pre;
}
il int get_next(int v) {
int id=root,nxt;
while(id) {
if(val[id]>v) nxt=val[id],id=ch[id][0];
else id=ch[id][1];
}
//解释同找前驱
return nxt;
}
P3369 【模板】普通*衡树(板子题)(Treap题解)(我的Treap代码)
二、\(Splay\)(伸展树)
理解了\(Tresp\)的旋转操作,\(Splay\)的旋转操作也可以如法炮制,这里就不放图了,直接上代码
il void rotate(int id) {
int father=fa[id],dir=get_dir(id);
//father是当前节点的父节点
//dir是当前节点属于其父节点的那个儿子
int g_father=fa[father];
//g_father是当前节点的祖父节点
ch[father][dir]=ch[id][dir^1];
fa[ch[father][dir]]=father;
ch[id][dir^1]=father;
fa[father]=id;
fa[id]=g_father;
if(g_father) {ch[g_father][ch[g_father][1]==father]=id;}//一定要注意!!!因为可能没有祖父节点,所以要先判断祖父节点的存在再连边
pushup(father);//更新
pushup(id);//更新
}
作为伸展树特有的方法,当然是其\(Splay\)操作了:将当前节点不断上旋直至根节点。
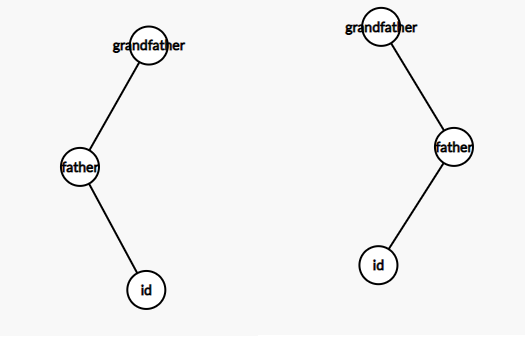
分为两种情况:
1.该节点与其父节点和其父节点与其祖父节点不共线:直接旋转即可。
情况如下图:
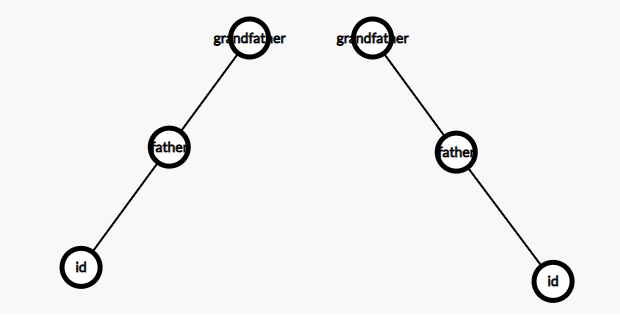
2.该节点与其父节点和其父节点与其祖父节点共线:先旋转父亲节点,再旋转该节点。
情况如下图:
我们可以来对比一下一直旋转\(id\)节点的效果和先旋转父节点再旋转\(id\)节点的效果。
一直旋转\(id\)节点:
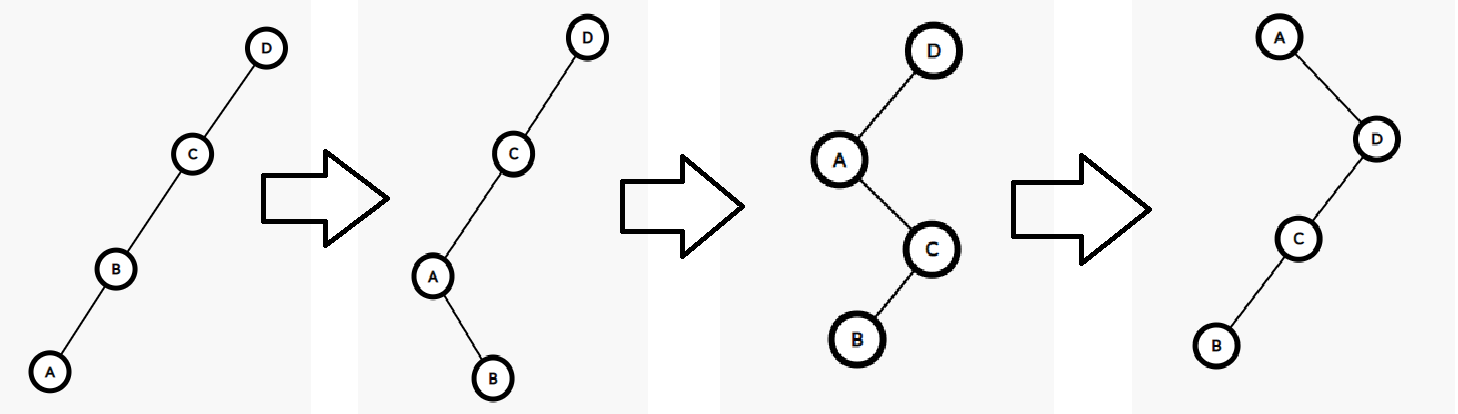
先旋转父节点再旋转\(id\)节点:
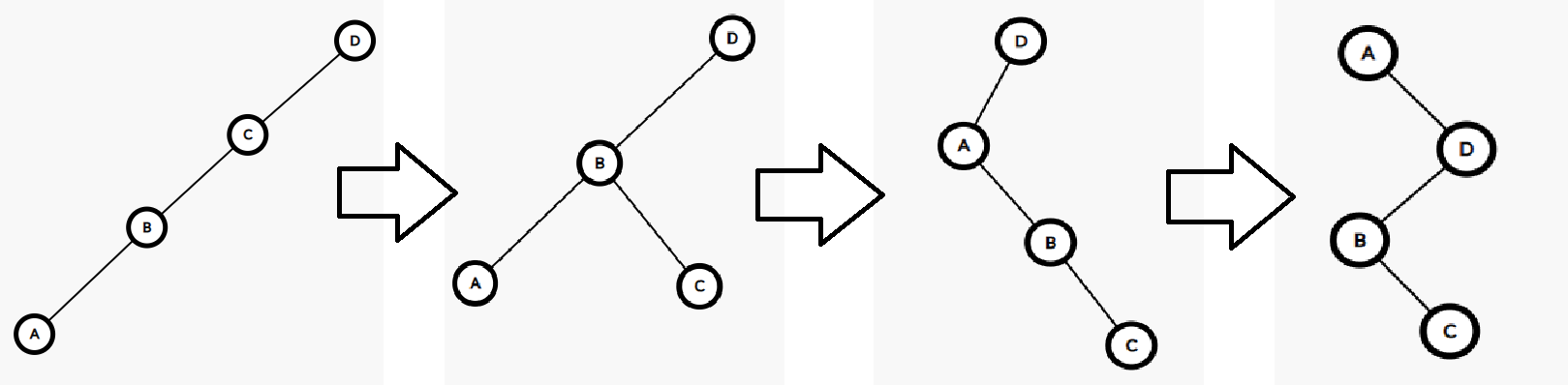
显然,先旋转父节点再旋转\(id\)节点会使树的深度减少一半,使树更加趋*于*衡。
最后再说点要注意的:每次进行有关点的操作时,都要进行一次\(Splay\),以保证树的随机性。
\(Thats\) \(all\),\(let's\) \(coding\)
const int N=1e5+10;
int n,whole_size,root;
int fa[N],cnt[N],val[N],ch[N][2],siz[N];
il void tree_clear(int id) {//清除该点
ch[id][0]=ch[id][1]=fa[id]=siz[id]=cnt[id]=val[id]=0;
}
il bool get_dir(int id) {//判断该点属于其父节点的那个儿子
return ch[fa[id]][1]==id;
}
il void pushup(int id) {//更新以id为根节点的子树的大小
if(id) {
siz[id]=cnt[id];
if(ch[id][0]) siz[id]+=siz[ch[id][0]];
if(ch[id][1]) siz[id]+=siz[ch[id][1]];
}
return ;
}
il void rotate(int id) {//旋转操作
int father=fa[id],dir=get_dir(id);
//father是当前节点的父节点
//dir是当前节点属于其父节点的那个儿子
int g_father=fa[father];
//g_father是当前节点的祖父节点
ch[father][dir]=ch[id][dir^1];
fa[ch[father][dir]]=father;
ch[id][dir^1]=father;
fa[father]=id;
fa[id]=g_father;
if(g_father) {ch[g_father][ch[g_father][1]==father]=id;}
//一定要注意!!!因为可能没有祖父节点,所以要先判断祖父节点的存在再连边(差错差了一上午,血淋淋的教训)
pushup(father);
pushup(id);
}
il void splay(int id) {
for(re int father;father=fa[id];rotate(id))
//因为一次可以判断到id的祖父节点,且不管共不共线最后都要旋转id
//所以将最后一次旋转放到循环结束之时
if(fa[father])
rotate(get_dir(id)==get_dir(father)?father:id);
//判断是否共线
root=id;//因为是直接旋转到根节点,所以更新根节点的编号为id
}
il void insert(int v) {//插入节点
if(!root) {//树中没有节点,建一个新点作为根节点
++whole_size;
root=whole_size;
ch[whole_size][0]=ch[whole_size][1]=fa[whole_size]=0;
siz[whole_size]=cnt[whole_size]=1;
val[whole_size]=v;
return ;
}
int now=root,father=0;
while(1) {
if(v==val[now]) {//找到该节点
++cnt[now];//增加其副本数
pushup(now);pushup(father);
splay(now);//把该节点旋转到根
break;
}
father=now;now=ch[now][val[now]<v];//判断往哪颗子树走
if(!now) {//树中没有该节点,新建一个
++whole_size;
ch[whole_size][0]=ch[whole_size][1]=0;
fa[whole_size]=father;
siz[whole_size]=cnt[whole_size]=1;
ch[father][val[father]<v]=whole_size;
val[whole_size]=v;
pushup(father);
splay(whole_size);
break;
}
}
}
il int find_rank(int v) {//根据节点的值找排名
int now=root,ans=0;
while(1) {
if(v<val[now]) now=ch[now][0];//往左子树走
else {
ans+=(ch[now][0]?siz[ch[now][0]]:0);//有左子树的话就加上左子树的大小
if(v==val[now]) {splay(now);return ans+1;}//如果是当前节点,就返回ans+1(这个1是因为该节点本身排一名)
ans+=cnt[now];//如果在右子树中,排名还要加上该节点的副本数
now=ch[now][1];//往右子树上走
}
}
}
il int find_val(int rank) {//根据节点排名找对应的值
int now=root;
while(1) {
if(ch[now][0]&&rank<=siz[ch[now][0]]) now=ch[now][0];
else {
int temp=(ch[now][0]?siz[ch[now][0]]:0)+cnt[now];
if(rank<=temp) return val[now];//因为该排名已经大于左子树的大小,又小于等于左子树和该节点副本数之和,所以答案就是当前节点的值
rank-=temp;//计算出其在右子树中的排名
now=ch[now][1];
}
}
}
//注:使用时应先插入val,再运行此函数,最后删去val
//因为插入时保证值为val的节点处在根节点,所以直接从根节点的左儿子一直往右走就是val的前驱
il int find_pre() {//找前驱
int now=ch[root][0];
while(ch[now][1]) now=ch[now][1];
return now;
}
//注:使用时应先插入val,再运行此函数,最后删去val
//因为插入时保证值为val的节点处在根节点,所以直接从根节点的右儿子一直往左走就是val的后继
il int find_nxt() {//求后继
int now=ch[root][1];
while(ch[now][0]) now=ch[now][0];
return now;
}
il void tree_delete(int v) {//删除值为val的节点
find_rank(v);//把该节点旋转到根节点
if(cnt[root]>1) {--cnt[root];pushup(root);return ;}//副本数大于1,直接减副本数
if(!ch[root][0]&&!ch[root][1]) {tree_clear(root);root=0;return ;}//是叶子节点,直接删
if(!ch[root][0]) {//没有左子树,用右子树直接代替该节点
int old_root=root;
root=ch[root][1];
fa[root]=0;
tree_clear(old_root);
return ;
}
if(!ch[root][1]) {//没有右子树,用左子树直接代替该节点
int old_root=root;
root=ch[root][0];
fa[root]=0;
tree_clear(old_root);
return ;
}
int left_max=find_pre(),old_root=root;
splay(left_max);//找该节点的前驱并把前驱旋转到根节点
//因为旋转完之后该节点一定没有左儿子(该节点是它前驱的后继),直接用该节点的右儿子代替该节点
ch[root][1]=ch[old_root][1];
fa[ch[old_root][1]]=root;
tree_clear(old_root);
pushup(root);
}
P3369 【模板】普通*衡树(板子题)(Splay题解)(我的Splay代码)
三、\(FHQ\) \(Treap\)
这是一种非旋转的\(Treap\),只需要通过分裂和合并两个简单的操作,就可以达到和其他*衡树一样的效果 (最重要的是终于不用调几百行的旋转函数了) ,既然它这么方便,那就赶紧学一下:
1.\(split\)
和它的名字一样,就是把一个\(Treap\)分成两个。
它有两种分法:按权值分裂和按排名分裂
权值版:
il void split(int id,int v,int &x,int &y) {
//注意这里的取地址符号,返回它分裂的两颗树的根节点
//id表示这棵树的根节点
//v表示按权值分裂
//x表示这颗树的左树,y表示这棵树的右树
if(!id) x=y=0;//这棵树没有节点,分完了
else {
if(val[id]<=v) x=id,split(ch[id][1],v,ch[id][1],y);
//该节点及其左子树都小于等于权值,全部分给左树
else y=id,split(ch[id][0],v,x,ch[id][0]);
//全部分给右树
pushup(id);
//更新节点大小
}
}
大小版:
il void split(int id,int rank,int &x,int &y) {
//注意这里的取地址符号,返回它分裂的两颗树的根节点
//id表示这棵树的根节点
//rank表示按排名分裂
//x表示这颗树的左树,y表示这棵树的右树
if(!id) x=y=0;//这棵树没有节点,分完了
else {
if(rank<=siz[ch[id][0]]) y=id,split(ch[id][0],rank,x,ch[id][0]);
//该节点及其右子树都大于等于排名,全部分给右树
else x=id,split(ch[id][1],rank-siz[ch[id][0]]-1,ch[id][1],y);
//全部分给左树
pushup(id);
//更新节点大小
}
}
2.\(merge\)
就是将两颗树合并,并返回合并后的根节点。
il int merge(int x,int y) {
if(!x||!y) return x+y;//有一颗子树为空的话,另一颗子树就是它的根节点
if(dat[x]<dat[y]) {//判断附加权值的大小,维护堆的性质
ch[x][1]=merge(ch[x][1],y);//因为x的附加权值更小,合并它的右儿子和y
pushup(x);//更新
return x;
}
else {
ch[y][0]=merge(x,ch[y][0]);////因为y的附加权值更小,合并它的左儿子和x
pushup(y);//更新
return y;
}
}
3.\(insert\)
把这棵树按权值分裂,再插入该权值即可。
split(root,v,x,y);
root=merge(merge(x,NEW(v)),y);
4.\(delete\)
把这棵树按权值\(v\)分为\(x\)、\(z\)两棵树,再按权值\(v-1\)分为\(x\)、\(y\)两棵树。
split(root,v,x,z);
split(x,v-1,x,y);
y=merge(ch[y][0],ch[y][1]);
root=merge(merge(x,y),z);
5.\(pre\)
找前驱时,把这棵树按权值\(v-1\)分裂,在左树中找最大值即可。
6.\(nxt\)
找后继时,把这棵树按权值\(v\)分裂,在右树中找最小值即可。
7.\(find\) \(rank\)
找排名时,把这棵树按权值\(v\)分裂,排名就是左树大小加\(1\)。
\(show\) \(you\) \(the\) \(whole\) \(code\)
#include <iostream>
#include <cstdio>
#include <cctype>
#include <cstdlib>
#define il inline
#define ll long long
#define int long long
#define re register
#define gc getchar
using namespace std;
//------------------------初始程序--------------------------
il int read(){
re int x=0;re bool f=0;re char ch=gc();
while(!isdigit(ch)){f|=ch=='-';ch=gc();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=gc();}
return f?-x:x;
}
il int max(int a,int b){
return a>b?a:b;
}
il int min(int a,int b){
return a<b?a:b;
}
//------------------------初始程序--------------------------
const int N=1e5+10;
int n,whole_size,root;
int val[N],dat[N],ch[N][2],siz[N];
il void pushup(int id) {//更新
if(id) {
siz[id]=1;
if(ch[id][0]) siz[id]+=siz[ch[id][0]];
if(ch[id][1]) siz[id]+=siz[ch[id][1]];
}
}
il int NEW(int v) {//新建节点
int id=++whole_size;
val[id]=v;
dat[id]=rand();
siz[id]=1;
return id;
}
il void split(int id,int v,int &x,int &y) {
//注意这里的取地址符号,返回它分裂的两颗树的根节点
//id表示这棵树的根节点
//v表示按权值分裂
//x表示这颗树的左树,y表示这棵树的右树
if(!id) x=y=0;//这棵树没有节点,分完了
else {
if(val[id]<=v) x=id,split(ch[id][1],v,ch[id][1],y);
//该节点及其左子树都小于等于权值,全部分给左树
else y=id,split(ch[id][0],v,x,ch[id][0]);
//全部分给右树
pushup(id);
//更新节点大小
}
}
il int merge(int x,int y) {
if(!x||!y) return x+y;//有一颗子树为空的话,另一颗子树就是它的根节点
if(dat[x]<dat[y]) {//判断附加权值的大小,维护堆的性质
ch[x][1]=merge(ch[x][1],y);//因为x的附加权值更小,合并它的右儿子和y
pushup(x);//更新
return x;
}
else {
ch[y][0]=merge(x,ch[y][0]);////因为y的附加权值更小,合并它的左儿子和x
pushup(y);//更新
return y;
}
}
il int find_id(int now,int rank) {//now是当前节点,根据排名找节点
while(1) {
if(rank<=siz[ch[now][0]]) now=ch[now][0];
else if(rank==siz[ch[now][0]]+1) return now;
else rank-=siz[ch[now][0]]+1,now=ch[now][1];
}
}
signed main()
{
int x=0,y=0,z=0;
n=read();
while(n--) {
int opt=read(),a=read();
if(opt==1) {//插入节点
split(root,a,x,y);
root=merge(merge(x,NEW(a)),y);
}
if(opt==2) {//删除节点
split(root,a,x,z);
split(x,a-1,x,y);
y=merge(ch[y][0],ch[y][1]);
root=merge(merge(x,y),z);
}
if(opt==3) {//查询排名
split(root,a-1,x,y);
printf("%lld\n",siz[x]+1);
root=merge(x,y);
}
if(opt==4) printf("%lld\n",val[find_id(root,a)]);//按排名查询值
if(opt==5) {//找前驱
split(root,a-1,x,y);
printf("%lld\n",val[find_id(x,siz[x])]);
root=merge(x,y);
}
if(opt==6) {//找后继
split(root,a,x,y);
printf("%lld\n",val[find_id(y,1)]);
root=merge(x,y);
}
}
return 0;
}
例题:
P2234 [HNOI2002]营业额统计(求前驱后继)(Treap题解)(我的Treap代码)
P3391 【模板】文艺*衡树(区间翻转)(Splay题解)(我的Splay代码)
P2042 [NOI2005] 维护数列(许多区间操作的*衡树)(Splay题解)(我的Splay代码)
P2286 [HNOI2004]宠物收养场(循环使用同一颗Splay)(Splay题解)(我的Splay代码)
P1486 [NOI2004] 郁闷的出纳员(Splay题解)(我的Splay代码)
本题区间操作都是对于整体进行,所以可以用一个变量记录而不用加tag标记,且由于要删除的节点都小于“最低工资\(-\)工资总变化量”,可以把它们移动到同一颗子树上再进行区间操作。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号