学习笔记——树链剖分

强烈推荐子谦dalao的树剖讲解

众所周知，树链剖分是一个让人称赞（毒瘤） 、学起来简单（从入门到入土）的数据结构。由于其应用范围十分广泛，所以十分值得OIer学习。

---

	好了，直接开始正题。

一、树剖的定义

    顾名思义，树剖就是将一棵树剖分成几条链，再用数据结构维护的过程。

二、树剖的几个概念

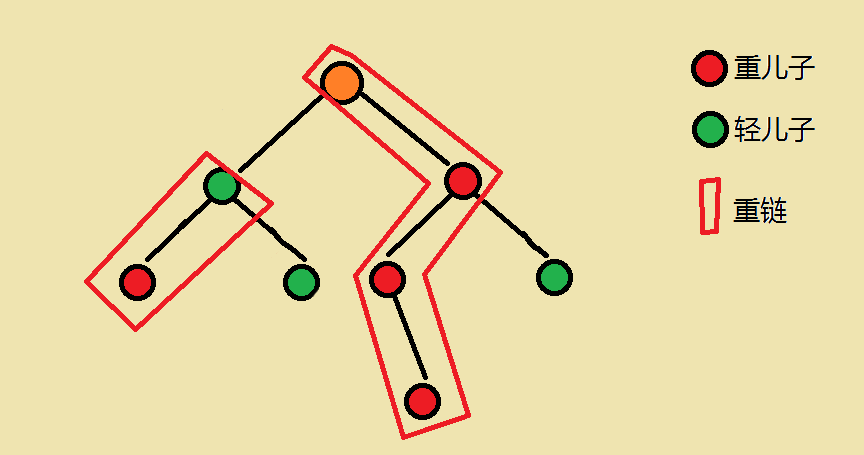
	重儿子：子树最大的儿子
	轻儿子：除了重儿子以外的儿子
	重边：父节点与重儿子组成的边
	轻边：除重边以外的边
	重链：重边连接而成的链
	轻链：轻边连接而成的链
	链头：一条链上深度最小的点

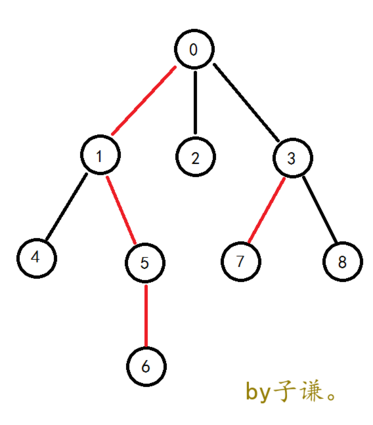
下面应用子谦dalao的一张图来解释

	图中的红色边即为重边，重边连成的链，与红色边相连的所有节点，即为重儿子，0节点即为链头

重链未必只有一条，每个子树都至少有一条重链。

三、树剖的相关操作

	修改点x到点y路径上各点的值
	查询点x到点y路径上各点的值
	修改点x子树上各点的值
	查询点x子树上各点的值

四、树剖的两个dfs

啊，我写不动了，直接上代码吧

int dep[MAXN],fa[MAXN],size[MAXN],son[MAXN];		//dep：深度，fa：父亲节点，size：子树大小，son：重儿子 
il void dfs(int u,int father)		//x为当前结点，f为父亲结点
{
	dep[u]=dep[father]+1;fa[u]=father;size[u]=1;
	for(R int i=head[u];i;i=e[i].next)
	{
		int to=e[i].to;
		if(to==father) continue;		//作为无向图，防止在父子结点中反复横跳
		dfs(to,u);
		size[u]+=size[to];		//显而易见，各个子树大小的和加上根这一结点就是此树的结点数
		if(size[to]>size[son[u]]) son[u]=to;		//不断比较求得重儿子 
	}
}

int top[MAXN],id[MAXN],pri[MAXN],dfstime;		//top：链顶节点，id：dfs序，pri：序号为dfs序的节点对应的原节点 
il void dfs1(int u,int topp)		//x为当前结点，topp是此链的开头结点
{
	top[u]=topp;id[u]=++dfstime;pri[dfstime]=u;
	if(son[u]) dfs1(son[u],topp);		//优先搜索重儿子，使其在线段树上成为一个连续的区间
	for(R int i=head[u];i;i=e[i].next)
	{
		int to=e[i].to;
		if(!top[to]) dfs1(to,to);		//搜索轻儿子，轻儿子的链头就是自己
	}
}

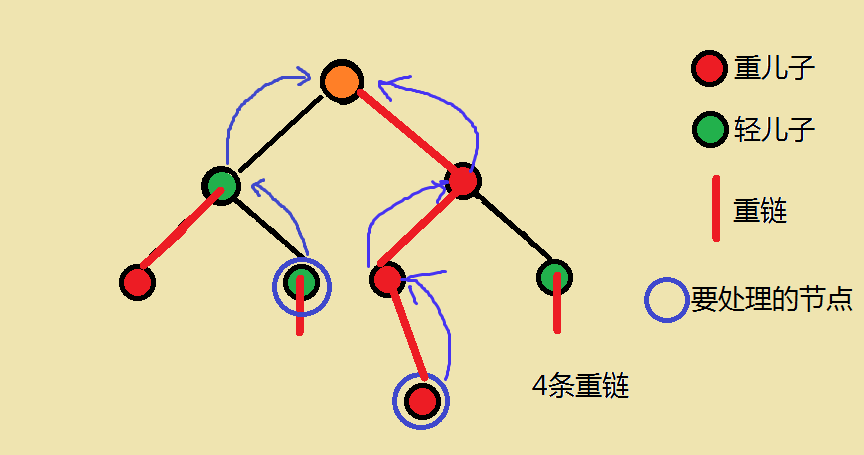
引用zengqinyi dalao的几张图来说明一下

	重点：dfs1的顺序是先处理重儿子再处理轻儿子，所以会有如下的图

    	这个图说明了一下两点
	 1.因为顺序是先重再轻，所以每一条重链的新编号是连续的
	 2.因为是dfs，所以每一个子树的新编号也是连续的

五、维护树剖的数据结构

默默地说（蒟蒻只会用线段树）
其实就是线段树的板子

struct w_tree{
	ll sum,lazy;
	ll l,r;
}tree[MAXN<<2];
il void pushup(int k)
{
	tree[k].sum=(tree[ls].sum+tree[rs].sum)%MOD;
}

il void build(int k,int l,int r)
{
	tree[k].l=l;tree[k].r=r;
	if(l==r)
	{
		tree[k].sum=w[pri[l]];
		tree[k].sum%=MOD;
		return ;
	}
	int mid=(l+r)>>1;
	build(ls,l,mid);build(rs,mid+1,r);
	pushup(k);
}

il void pushdown(int k,len)
{
	tree[ls].lazy+=tree[k].lazy;tree[ls].lazy%=MOD;
	tree[rs].lazy+=tree[k].lazy;tree[rs].lazy%=MOD;
	tree[ls].sum+=(tree[k].lazy*((len+1)>>1)%MOD;
	tree[rs].sum+=(tree[k].lazy*(len>>1)%MOD;
	tree[ls].sum%=MOD;tree[rs].sum%=MOD;
	tree[k].lazy=0;
}

il void change(int k,int x,int y,int val)
{
	int mid=(tree[k].l+tree[k].r)>>1,len=(tree[k].r-tree[k].l+1);
	if(x<=tree[k].l&&tree[k].r<=y)
	{
		tree[k].lazy+=val;tree[k].lazy%=MOD;
		tree[k].sum+=val*len;tree[k].sum%=MOD;
		return ;
	}
	if(tree[k].lazy) pushdown(k,len);
	if(x<=mid) change(ls,x,y,val);
	if(mid<y) change(rs,x,y,val);
	pushup(k);
}

il ll ask(int k,int x,int y)
{
	if(x<=tree[k].l&&tree[k].r<=y) return tree[k].sum%MOD;
	ll ans=0;
	int mid=(tree[k].l+tree[k].r)>>1,len=(tree[k].r-tree[k].l+1);
	if(tree[k].lazy) pushdown(k,len);
	if(x<=mid) ans+=ask(ls,x,y);
	if(mid<y) ans+=ask(rs,x,y);
	return ans%MOD;
}

update: 2020.10.23
还有一种线段树的写法

#define ls (k<<1)
#define rs ((k<<1)|1) 
struct w_tree{
	int l,r;
	ll lazy,sum;
}tree[MAXN<<2];
il void pushup(int k)
{
	tree[k].sum=tree[ls].sum+tree[rs].sum;
}

il void build(int k,int l,int r)
{
	tree[k].l=l;tree[k].r=r;
	if(l==r)
	{
		tree[k].sum=w[pri[l]];
		return ;
	}
	int mid=(l+r)>>1;
	build(ls,l,mid);build(rs,mid+1,r);
	pushup(k);
}

il void pushdown(int k)
{
	tree[ls].lazy+=tree[k].lazy;
	tree[rs].lazy+=tree[k].lazy;
	tree[ls].sum+=(tree[ls].r-tree[ls].l+1)*tree[k].lazy;
	tree[rs].sum+=(tree[rs].r-tree[rs].l+1)*tree[k].lazy;
	tree[k].lazy=0;
}

il void change(int k,int x,int y,int val)
{
	int l=tree[k].l,r=tree[k].r;
	if(y<l||r<x) return ;
	if(x<=l&&r<=y)
	{
		tree[k].lazy+=val;
		tree[k].sum+=val*(r-l+1);
		return ;
	}
	if(tree[k].lazy) pushdown(k);
	change(ls,x,y,val);change(rs,x,y,val);
	pushup(k);
}

il ll ask(int k,int x,int y)
{
	int l=tree[k].l,r=tree[k].r;
	if(y<l||r<x) return 0;
	if(x<=l&&r<=y) return tree[k].sum;
	if(tree[k].lazy) pushdown(k);
	return ask(ls,x,y)+ask(rs,x,y);
}

六、树剖的操作函数

il void operate1(int x,int y,int val)		//修改点x到点y路径上各点的值
{
	val%=MOD;
	while(top[x]!=top[y])		//寻找LCA的过程
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);		//保证x为深度最深的节点
		change(1,id[top[x]],id[x],val);		//更新x向上爬时所经过的所有点的点权
		x=fa[top[x]];		//将深度较深的节点往上爬
	}
	if(dep[x]>dep[y]) swap(x,y);		//保证x的深更小，以便修改线段树上的连续区间
	change(1,id[x],id[y],val);		//常规的修改区间
}

//操作二和一一样（也就两行的差别）
il ll operate2(int x,int y)			//查询点x到点y路径上各点的值
{
	ll ans=0;
	while(top[x]!=top[y])
	{
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		ans+=ask(1,id[top[x]],id[x]);ans%=MOD;
		x=fa[top[x]];
	}
	if(dep[x]>dep[y]) swap(x,y);
	ans+=ask(1,id[x],id[y]);
	return ans%MOD;
}

//因为我们已经把子树存为线段树上的连续区间了，直接修改从x到size【x】的所有值即可
il void operate3(int x,int val)			//修改点x子树上各点的值
{
	change(1,id[x],id[x]+size[x]-1,val);
}

il ll operate4(int x)		//查询点x子树上各点的值
{
	return ask(1,id[x],id[x]+size[x]-1)%MOD;
}

看图说话，就是

七、好，我宣布，本博客到此完结（完结撒花）