学习笔记——AC自动机
前言
\(AC\)自动机的题相对而言较为套路,但重在理解其思维,了解每一个数组的含义及一些拓展用法,就可以了。(模板一定要打对,不然真就成\(WA\)自动机了)
\(AC\)自动机的一些概念
我们都知道,\(KMP\)用于解决单模式串与多文本串的匹配问题,\(Trie\)树用于实现字符串快速检索,\(AC\)自动机就是两者的结合,用于解决多模式串匹配问题。
首先,我们可以仿照\(Trie\)树,将每一个模式串都插入到\(Trie\)树上,再在\(Trie\)树上建立失配数组,然后按照正常的\(Trie\)树检索和\(KMP\)匹配失配指针的方式和文本串进行匹配即可。
1.建立\(AC\)自动机
char str[N];
int trie[N][26],end[N],fail[N],cnt=0;
//trie就是trie树的数组,end就是记录结尾节点的数组,fail就是失配数组
il void insert() {
scanf("%s",str+1);
int id=0,len=strlen(str+1);
for(re int i=1;i<=len;++i) {
int to=str[i]-'a';
if(!trie[id][to]) trie[id][to]=++cnt;
id=trie[id][to];
}
++end[id];
}
//同Trie的建树操作
2.构建失配数组
il void get_fail() {
queue <int> q;//存Trie树上的节点
for(re int i=0;i<26;++i) {
if(trie[0][i]) //如果有这个点,就加入队列
q.push(trie[0][i]);
//如果trie树的起点不是0,是st,还要加一句fail[trie[0][i]]=st
}
while(!q.empty()) {
int u=q.front();q.pop();
for(re int i=0;i<26;++i) {
if(trie[u][i]) {
fail[trie[u][i]]=trie[fail[u]][i];
//从u节点更新其儿子节点的失配指针
//其儿子节点的失配指针指向u节点的失配指针指向的节点的边权相同的节点
//此处不用一直跳fail指针,因为u节点的fail指针更新先于其儿子的fail指针
q.push(trie[u][i]);
//有这个点,就加入队列
}
else trie[u][i]=trie[fail[u]][i];
//没有这个点,就把这个点变为u节点失配指针指向的边权相同的点
}
}
}
这一步是\(AC\)自动机的精髓,光看代码可能还是比较难理解,下面给张图解释一下:
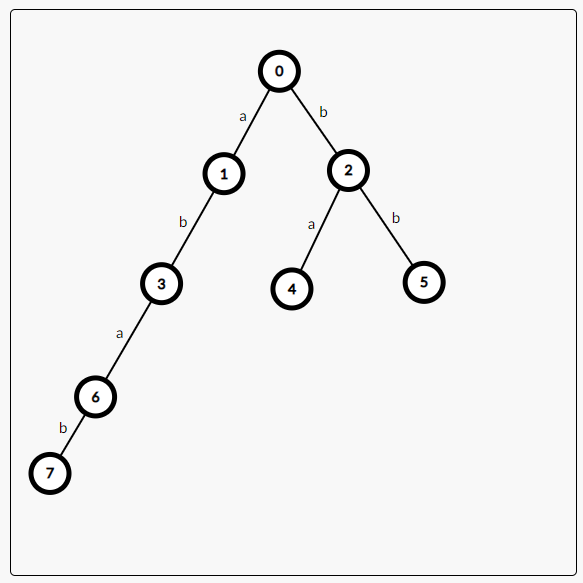
这是我们插入\(Trie\)树中的文本串
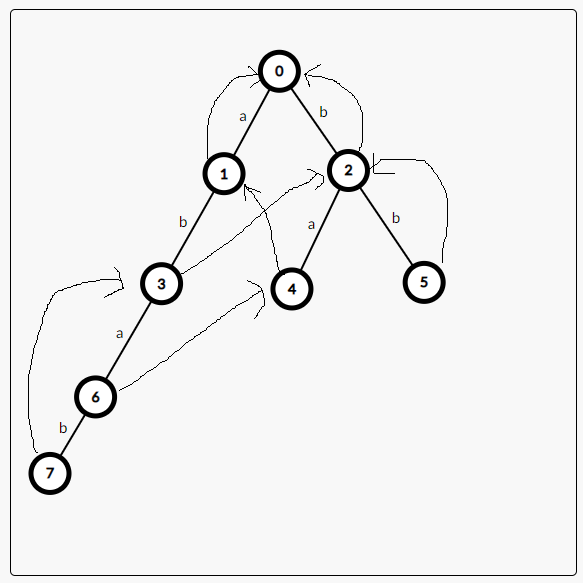
这里的虚线就是该节点的失配指针,类似\(KMP\),当匹配失配时,我们可以通过跳\(fail\)来重新匹配,将字符串匹配复杂度降低。(还是不会用画图软件,将就看吧)
3.查询操作
以下代码为查询模式串在文本串中的出现次数。
il int ask() {
scanf("%s",str+1);//输入文本串
int id=0,len=strlen(str+1),res=0;
for(re int i=1;i<=len;++i) {
int to=str[i]-'a';
id=trie[id][to];
for(re int j=id;j&&end[j]!=-1;j=fail[j])
//跳fail指针,看是不是一个模式串的结束节点
res+=end[j],end[j]=-1;
//是就统计答案,并清空防止以后再被访问到
}
return res;
}
下面就是\(AC\)自动机的完整代码了:
#include <iostream>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <queue>
#define il inline
#define ll long long
#define int long long
#define re register
#define gc getchar
using namespace std;
//------------------------初始程序--------------------------
il int read(){
re int x=0;re bool f=0;re char ch=gc();
while(!isdigit(ch)){f|=ch=='-';ch=gc();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+(ch^48);ch=gc();}
return f?-x:x;
}
il int max(int a,int b){
return a>b?a:b;
}
il int min(int a,int b){
return a<b?a:b;
}
//------------------------初始程序--------------------------
const int N=1e6+10;
int n;
char str[N];
int trie[N][26],end[N],fail[N],cnt=0;
//trie就是trie树的数组,end就是记录结尾节点的数组,fail就是失配数组
il void insert() {
scanf("%s",str+1);
int id=0,len=strlen(str+1);
for(re int i=1;i<=len;++i) {
int to=str[i]-'a';
if(!trie[id][to]) trie[id][to]=++cnt;
id=trie[id][to];
}
++end[id];
}
il void get_fail() {
queue <int> q;//存Trie树上的节点
for(re int i=0;i<26;++i) {
if(trie[0][i]) //如果有这个点,就加入队列
q.push(trie[0][i]);
//如果trie树的起点不是0,是st,还要加一句fail[trie[0][i]]=st
}
while(!q.empty()) {
int u=q.front();q.pop();
for(re int i=0;i<26;++i) {
if(trie[u][i]) {
fail[trie[u][i]]=trie[fail[u]][i];
//从u节点更新其儿子节点的失配指针
//其儿子节点的失配指针指向u节点的失配指针指向的节点的边权相同的节点
//此处不用一直跳fail指针,因为u节点的fail指针更新先于其儿子的fail指针
q.push(trie[u][i]);
//有这个点,就加入队列
}
else trie[u][i]=trie[fail[u]][i];
//没有这个点,就把这个点变为u节点失配指针指向的边权相同的点
}
}
}
il int ask() {
scanf("%s",str+1);//输入文本串
int id=0,len=strlen(str+1),res=0;
for(re int i=1;i<=len;++i) {
int to=str[i]-'a';
id=trie[id][to];
for(re int j=id;j&&end[j]!=-1;j=fail[j])
//跳fail指针,看是不是一个模式串的结束节点
res+=end[j],end[j]=-1;
//是就统计答案,并清空防止以后再被访问到
}
return res;
}
signed main()
{
n=read();
for(re int i=1;i<=n;++i) insert();
get_fail();
printf("%lld\n",ask());
return 0;
}
接下来,我们就可以开始我们的刷题之路了:
P3808 【模板】AC自动机(简单版)(学习代码的题解)(有图讲解的题解)(我的代码)
P3796 【模板】AC自动机(加强版)(题解)(我的代码)
修改查询函数,改为记录模式串出现次数,最后\(sort\)一遍把出现次数相同的最长的字符串输出即可。
P5357 【模板】AC自动机(二次加强版)(题解)(我的代码)
本题要对\(fail\)数组进行理解,将其建成一颗\(fail\)树,统计\(Trie\)的终止节点在\(fail\)树的子树上的总匹配次数。
理解:因为\(fail\)树的一个节点的子树的所有节点都可以通过失配指针跳到当前节点,所以他们都有相同的前缀(从\(trie\)树的根节点到该节点),所以模式串出现次数就是\(fail\)树上该节点子树的文本串出现次数。
P3121 [USACO15FEB]Censoring G(题解)(我的代码)
本题要运用栈的思想,分别记录\(AC\)自动机扫到的节点和合法的字符,如果\(AC\)自动机匹配到了就将两个栈同时弹出匹配到的长度,最后输出合法字符栈内的字符即可。
本题是\(AC\)自动机二次加强版的板子,只要改一下模式串就可以得到结果(双倍经验)
P3041 [USACO12JAN]Video Game G(题解)(我的代码)
本题是\(AC\)自动机\(+ DP\),我们用\(dp[i][j]\)表示长度为\(i\)的字符串在\(Trie\)树上编号为\(j\)的节点结束的最大得分,再枚举下一个是\(ABC\)三选一的情况时的匹配次数,找哪个贡献最大,最后取长度为\(k\)时的最大值即可。
P4052 [JSOI2007]文本生成器(题解)(我的代码)
本题同样是\(AC\)自动机\(+ DP\),我们用\(dp[i][j]\)表示长度为\(i\)且结束节点为\(j\)的不合法字符串数(没有走到一个字符串的结束节点),再运用容斥原理用总数减去长度为\(m\)的所有不合法字符串总数即可。
本题要找无限长的可行串,我们可以转化一个思路:将\(Trie\)树连向儿子节点的边看做单向边,再将该节点连向其失配节点的边看做单向边,再在\(Trie\)树上找环(该环不能经过任意病毒串的结束节点),找的到就有无限长的可行串。(因为可以一直绕着那个环走)
因为以上是两道一样的题,所以给一个提供思路的题解,只要处理一下不同的输入方式即可。
思路:因为要判断第\(x\)个字符串在第\(y\)个字符串中出现的次数,所以我们可以构造一颗\(fail\)树,判断以\(x\)的结束节点为根的子树中,有多少个节点属于\(y\)字符串(因为如果\(y\)字符串的\(fail\)指针指向\(x\)字符串,那么\(x\)字符串一定在\(y\)字符串中出现过(可结合上面的\(fail\)树图进行理解)),对于这个问题,我们可以运用树链剖分的思想,将\(fail\)树的每一个节点标记一个\(dfs\)序,并统计每一个节点的子树大小,那么\(u\)节点子树对应的区间就是\([dfn[u],dfn[u]+siz[u]-1]\),用树状数组维护即可。
刷题题单
参考资料
《信息学奥赛一本通提高篇》



 浙公网安备 33010602011771号
浙公网安备 33010602011771号