微积分初步

前言

luogu

吾有一友，他叫导哥。我很菜，有些人可能觉得这是一眼题。有问题欢迎私信，会获得我的膜拜和关注qwq

适合那些会一些导数的人

---

上面都是初二时候写的hhh

高二数学上到导数，发现之前学的其实很简单啊，而且现在有更厉害的工具了，再证一下吧

原标题为关于导数问题的一些粗浅思考，因为加入了微积的部分，所以标题就是微积分初步

---

em首先将导数的运算证明一下吧qwq

前置知识

极限

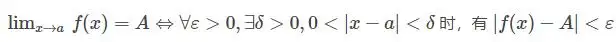
这也是极限的 \(ε-δ\) 语言，意思大概就是，如果对于一个值 \(A\)，对于所有正数 \(ε\)，都存在一个 \(x\) 周围的区域满足，函数值在 \(A\) 附近，很好理解，注意中间有个充要的这个条件

同样的，我们用 \(ε-δ\) 语言也可以定义函数连续，大概思路就是这个函数存在一个区域使得周围都和这个函数值小于任意正数

重要极限

1. \(\lim\limits_{x->0} \frac{\sin x}{x}=1\)

   龙崎上课用的夹逼好像和我不一样？

   

2. \(e=\lim\limits_{n->0}(1+n)^{\frac{1}{n}}\)

我们证明两个东西，一个是这个东西对于 \(n\) 单增，一个是这个东西有界，那么这个东西就有极限

对于单增，我们将 \((1+\frac{1}{n})^{n}\) 看作 \(n\) 个 \(1+\frac{1}{n}\) 和一个 \(1\) 相乘，那么有不等式算术平均数大于等于几何平均数 \(\frac{n(1+\frac{1}{n})+1}{n+1}\ge ((1+\frac{1}{n})^{n}·1)^{\frac{1}{n+1}}\)

\((1+\frac{1}{n+1})^{n+1}\ge ((1+\frac{1}{n})^{n}·1)\)

对于有界的证明，我们使用二项式定理 \(e=\lim\limits_{n->infty}\sum_{i=0}^{n} {n\choose i} \frac{1}{n}^{i}=1+1+\lim\limits_{n->infty}\sum_{i=2}^{n} {n\choose i} \frac{n(n-1)\dots (n-i+1)}{i!n^{i}}\)

对于右边进行放缩，我们把式子往大了放把 \(\frac{1}{n^{i}}\) 和 \(n(n-1)\dots(n-i+1)\) 消掉，变成

\(原式<2+\lim\limits_{n->\infty} \sum_{i=2}^{n} \frac{1}{i!}\)

继续往大放

\(原式<2+\lim\limits_{n->\infty} \sum{i=2}^{n} \frac{1}{i*(i-1)}\)

\(原式<2+\sum_{i=2}^{n} \frac{1}{i-1}-\frac{1}{i}\)

\(原式<2+1-\frac{1}{n}\)

所以上界就是3。既然我们有了一个比较松的上界，就和那个质数间隔一样（大概就是这个意思），我们前面放的项数再多一点，就能得到更紧的上界

一些求导法则

复合函数求导

\(f(g(x))\) 对于 \(x\) 的导数等于 \(f(g(x))\) 对于 \(g(x)\) 的导数乘上 \(g(x)\) 对于 \(x\) 的导数，\(\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}\)

这就是链式法则，很好理解。

反函数求导

1. 比如说是 \(y=\log_{a}x\)

   \(x=a^{y}\)

   \(\frac{dx}{dy}=a^{y}\ln a\)

   \(\frac{dy}{dx}=\frac{1}{a^{y}\ln a}\)

   \(\frac{dy}{dx}=\frac{1}{x\ln a}\)

2. 再比如 \(y=x^{\frac{1}{n}}\)
   \(y^{n}=x\)

   \(\frac{dx}{dy}=ny^{n-1}\)

   \(\frac{dy}{dx}=\frac{1}{ny^{n-1}}\)

   \(\frac{dy}{dx}=\frac{1}{nx^\frac{n-1}{n}}\)

   \(\frac{dy}{dx}=\frac{1}{n}x^{\frac{1}{n}-1}\)

所以我们可以总结大概的方法，也就是原函数求个导，然后分子分母倒一下

导数的四则运算

1.\([f(x)\pm g(x)]^{'}=f(x)^{'}\pm g(x)^{'}\)(懒，易证)

2.\([f(x)* g(x)]^{'}\)

\(= \lim_{\Delta {x} \to {0}} \frac{f(x+\Delta {x})*g(x+\Delta {x})-f(x)*g(x)}{\Delta {x}}\)

设\(f(x+\Delta x)=a,g(x+\Delta x)=b,f(x)=c,g(x)=d\)

\(\therefore =\frac{ab-ad+ad-cd}{\Delta x}\)

\(=\frac{a(b-d)}{\Delta x}+\frac{d(a-c)}{\Delta x}\)

\(=f(x)^{'}*g(x)+g(x)^{'}*f(x)\)

3.\([\frac {f(x)}{g(x)}]^{'}\)

\(= [f(x)* \frac{1}{g(x)}]^{'}\)

\(=f(x)^{'}*\frac{1}{g(x)}+f(x)*\frac{1}{g(x)}^{'}\)

求\(\frac{1}{g(x)}^{'}\)(或者用\(f(x^{a})^{'}=ax^{a-1}\),但这个还没证)

\(=\lim_{\Delta x \to 0}\frac{\frac{1}{g(x+\Delta x)}-\frac{1}{g(x)}}{\Delta x}\)

\(=\lim_{\Delta x \to 0}\frac{g(x)-g(x+\Delta x)}{\Delta x*g(x)*g(x+\Delta x)}\)(观察到整体)

\(=-\frac{g(x)^{'}}{g(x)^{2}}\)

\(\therefore原式=f(x)^{'}*\frac{1}{g(x)}-f(x)*\frac{g(x)^{'}}{g(x)^{2}}\)

\(=\frac{f(x)^{'}*g(x)-g(x)^{'}*f(x)}{g(x)^{2}}\)

下面是一些基本函数的导数

1.\((x^{n})^{'}=nx^{n-1}\)

法一：

对于实数都成立，因为是广义二项式定理

法二：

先证明指数是 \(\frac{1}{n}\) 的情况，从而证明完有理数的情况，然后用极限把实数逼近成有理数，然后就好了

1.\((\sin x)^{'}=\cos x\) 和 \((\cos x)^{'}=\sin x\)

\((\sin x)^{'}=\lim_{\Delta x \to 0} \frac{\sin(x+\Delta x)-\sin(x)}{\Delta x}\)

\(=\lim_{\Delta x \to 0} \frac{2\cos(x+\frac{\Delta x}{2})\sin(\frac{\Delta x}{2})}{\Delta x}\)(和差化积)

\(=\lim_{\Delta x \to 0} \frac{\cos(x+\frac{\Delta x}{2})\sin(\frac{\Delta x}{2})}{\frac{\Delta x}{2}}\)

\(=\lim_{\Delta x \to 0} \cos(x+\frac{\Delta x}{2})\)

\(=\cos(x)\)

\((\cos x)^{'}=\lim_{\Delta x \to 0} \frac{\cos(x+\Delta x)-\cos(x)}{\Delta x}\)

\((\cos x)^{'}=\lim_{\Delta x \to 0} \frac{-2\sin(x+\frac{\Delta x}{2})sin(\frac{\Delta x}{2})}{\Delta x}\)(故技重施)

\((\cos x)^{'}=-\sin(x)\)

2.\((e^{x})^{'}=e^{x}\)

\(\because e=\lim_{x \to \infty} (1+\frac{1}{x})^{x}\)

\(\therefore e=\lim_{x \to 0} (1+x)^{\frac{1}{x}}\)(将\(x\)替换为它的倒数)

\(\therefore \ln \lim_{x \to 0}(1+x)^{\frac{1}{x}}=1\)

\(\therefore \lim_{x \to 0}\frac{\ln (1+x)}{x}=1\)

\((e^{x})^{'}=\lim_{x \to 0} \frac{e^{x+\Delta x}-e^{x}}{\Delta x}\)

\(=\lim_{x \to 0}e^{x}*\frac{e^{\Delta x}-1}{\Delta x}\)

设\(t=e^{\Delta x}-1\)

则 \(\Delta x=\ln (t+1)\)

\(=\lim_{t \to 0}e^{x}*\frac{t}{\ln (t+1)}\)

\(=e^{x}\)

\(3.(a^{x})^{'}=a^{x}\ln a\)

\(\lim_{\Delta x \to 0} \frac{a^{x+\Delta x}-a^{x}}{\Delta x}\)

\(=\lim_{\Delta x \to 0} a^{x}*\frac{a^{\Delta x}-1}{\Delta x}\)

设\(a^{\Delta x}-1=t\)

则\(\Delta x=\log_{a}{(t+1)}=\frac{\ln(t+1)}{\ln a}\)

\(\therefore 原式=\lim_{t \to 0} a^{x}*\frac{t*\ln a}{\ln (t+1)}\)

\(=a^{x}\ln a\)(故技重施)

\(4.(\ln x)^{'}=\frac{1}{x}\)

法一：

\(=\lim_{\Delta x \to 0}\frac{\ln (x+\Delta x)-ln(x)}{\Delta x}\)

\(=\lim_{\Delta x \to 0} \frac{\ln (1+\frac{\Delta x}{x})-ln(1)}{\Delta x*x}\)

\(=\lim_{\Delta x \to 0} \frac{1}{x}\)(观察到整体，故技重施)

法二：

反函数求导

\(5.log_{a}{x}^{'}=\frac{1}{x\ln a}\)

法一：

\(=(\frac{\ln x}{\ln a})^{'}\)

\(=\frac{\frac{1}{x}}{\ln a}(\ln a\)为常数)

\(=\frac{1}{x\ln a}\)

法二：

反函数求导

中值定理

导数运算

首先看到一道题:

已知\(f(x)=\frac{(x+1)^{2}+\sin x}{x^{2}+1}\)，求\(f(2020)+f^{'}(2020)+f(-2020)- f^{'}(-2020)\)

对于这种比较大的，考虑根据奇偶性判断。

\(f(x)=\frac{(x+1)^{2}+\sin x}{x^{2}+1}\)

\(=1+\frac{2x+\sin x}{x^{2}+1}\)

\(\because y=2x\)为奇函数，\(y=\sin x\)为奇函数,\(y=x^{2}+1\)为偶函数

\(\therefore y=\frac{2x+\sin x}{x^{2}+1}\)为奇函数

\(\therefore f(2020)-1=-f(2020)-1\)

\(\therefore f(2020)=-f(2020)\)

\(\because\) 奇函数的导函数为偶函数

\(f^{'}(2020)=f^{'}(-2020)\)

所以原式\(=2\)

再来看切线问题:

我觉得这就是靠列方程暴算

首先看到一道题:

若曲线\(y_{1}=ax^{2}\)与曲线\(y_{2}=\ln x\)在公共点有公切线,求\(a\)

模拟题意可得

\(\{\begin{matrix} 1.2ax=\frac{1}{x}\\ \ \ \ 2.ax^{2}=\ln x \end{matrix}.\)

将1带入2

\(\ln x=\frac{1}{2}\)

\(x=\sqrt{e}\)

\(\therefore a=\frac{1}{2e}\)

其次看到一道题:

若直线\(y=kx+b\)是曲线\(y=e^{x}\)的切线，也是曲线\(y=\ln(x+2)\)的切线,求k

模拟题意可得

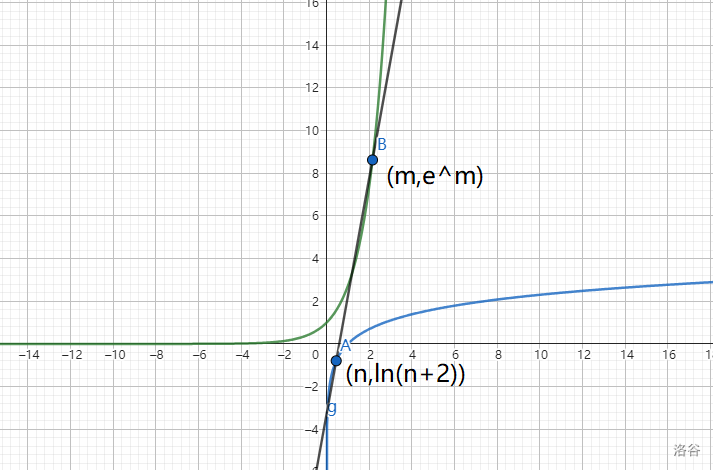
\(\{\begin{matrix} 1.e^{m}=k\\ 2.\frac{1}{n+2}=k\\ 3.km+b=e^{m}\\ 4.kn+b=\ln (n+2) \end{matrix}.\)

天哪，有四个方程怎么办,carbon见到这个便说不会做，但四元4个方程这显然是可以做的

显然n最好消。

\(\{\begin{matrix} 1.e^{m}=k\\ 2.km+b=e^{m}\\ 3.1-2k+b=\ln (\frac{1}{k}) \end{matrix}.\)

消b

\(\{\begin{matrix} 1.e^{m}=k\\ 2.1-2k+e^{m}-km=\ln (\frac{1}{k}) \end{matrix}.\)

将1代入2得

\(\{\begin{matrix} 1.e^{m}=k\\ 2.1-k-km=\ln (\frac{1}{k}) \end{matrix}.\)

化简2得

\(e^{1-k-km}=\frac{1}{k}\)

\(\frac{e}{e^{k}*(e^{m})^{k}}=\frac{1}{k}\)

\(\frac{e}{e^{k}*k^{k}}=\frac{1}{k}\)

\(e=e^{k}*k^{k-1}\)

\((e*k)^{k-1}=1\)

\(\therefore k=1\)或\(k=\frac{1}{e}\)

利用导数求最值

首先解释下为什么可以(用反证法即可)

求出来的是最大值或最小值

首先看到一道题:

若\(\frac{a^{2}-\ln a}{b}=\frac{c-2}{d}=1\),求\((a-c)^{2}+(b-d)^{2}\)的最小值。

这是一道5星题，但其实非常简单。

首先看到\((a-c)^{2}+(b-d)^{2}\)可以想到两点间的距离，之后就很简单了

得到两个函数

\(\{\begin{matrix} 1.b=a^{2}-\ln a\\ 2.d=c-2 \end{matrix}.\)

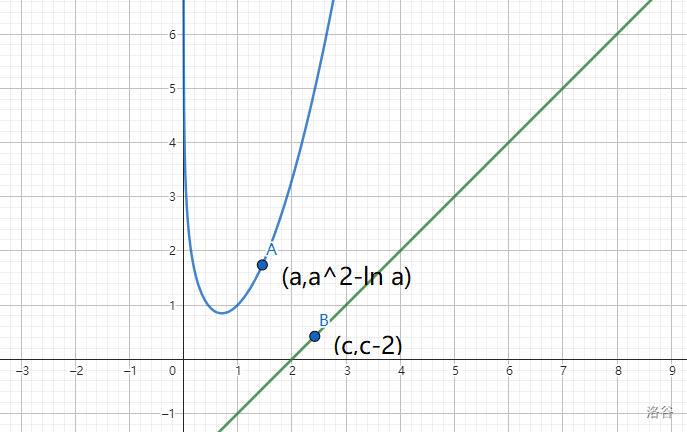
求个导，导数一样

\(2a-\frac{1}{a}=1\)

\(a_{1}=1,a_{2}=-\frac{1}{2}\)(舍)

带回去就是 \(2\) 了