分类问题的一些记录
01逻辑回归问题
1.1 对于二分类问题
在输出时我们希望输出一个0-1之间的概率,而不希望存在负数。这时候在最后一层的激活函数我们可以考虑利用sigmoid函数,其图如下:
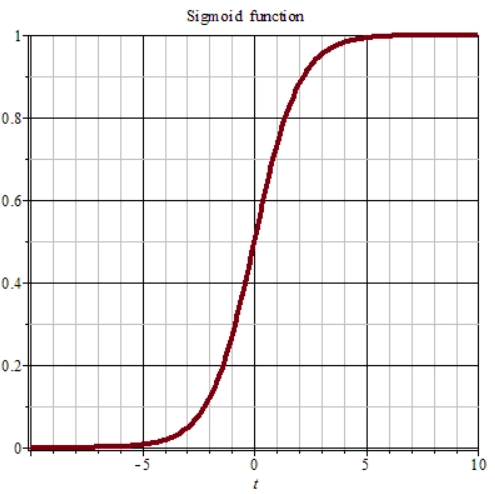
对于二分类的损失函数是这样定义的
其中\(y\)是真实值,\(\hat{y}\)是预测值;
当\(y=1\)时,损失函数\(loss=-ylog(\hat{y})\),如果想要损失函数\(loss\)尽可能得小,那么,\(\hat{y}\)就要尽可能大,因为sigmoid函数取值 [0,1],所以\(\hat{y}\)会无限接近于1。
当\(y=0\)时,损失函数\(loss=-(1-y)log(1-\hat{y} )\),如果想要损失函数\(loss\)尽可能得小,那么,\(\hat{y}\)就要尽可能小,因为sigmoid函数取值 [0,1],所以\(\hat{y}\)会无限接近于0。
1.2对于多分类问题
多分类问题的真实标签一般采用one-hot编码,也即对应的输出结果存在多个,那么如何量化损失函数呢?我们肯定也希望输出的结果中对应准确类别的概率越高越好,这时我们就用到了softmax,这个函数能够将越策的多个输出的值进行归一化,使输出的所属所有类别的概率相加等于1。下面是softmax的公式:
对输出的概率进行归一化后,对于损失函数,我们希望真实标签对应的输出概率最大,故可以用$ loss(y,\hat{y})= {\textstyle \sum_{i}y_{i} log(\hat{y_{i}})} $进行量化。
对于分类问题:就是如果\(y\)等于1,我们就尽可能让 \(\hat{y}\)变大,如果 \(y\) 等于0,我们就尽可能让\(\hat{y}\)变小。
02信息熵
自信息
信息论的基本想法是一个不太可能的事情居然发生了,要比一个可能的事情发生,提供更多的信息。
信息论中定义了一个自信息:\(I(x)=-logP(x)\).然而,这个定义只能描述单个事件所蕴含的信息(如一个专家预测地球爆炸的概率为P(x))。但是这一个专家也不一定准啊,也是有了信息熵。
信息熵是离散随机事件自信息得到期望。
\(H(x)=-P(x_{i})\sum_{i} logP(x_{i})\)
举了例子,加入超人联盟的课题组3个专家给出的地球爆炸的概率为0.3,0.2,0.3,而翠纽币组3个专家给出的地球爆炸的概率为0.4,0.8,0.9。
则从超人联盟中得出的信息熵为0.45
而翠纽币组得出的信息熵为0.27;从结果中可以看出超人联盟中给出的地球爆炸蕴含的信息量比较多,也就是不确定因素也比较多,而翠纽币组给出的信息量少,也就确定性因素比较大。
03相对熵(KL散度)
KL散度:是衡量两个概率分布差异的非对称性度量。
通俗说法:KL散度就是用来衡量同一个随机变量的两个不同分布之间的距离。
$D_{kl}(p || q)=\sum_{i=1}^{n}p(x_{i})log(\frac{p(x_{i})}{q(x_{i})}) $
特性:
- 非对称性
\(D_{kl}(p || q)\neD_{kl}(q || p)\) 仅当p和q的概率分布完全一样才相等。 - 非负性
\(D_{kl}(p || q)>0\) 仅当p和q的概率分布完全一样才相等0。
如上例子:
超人联盟相对翠纽币组的散度为0.37
而翠纽币组相对超人联盟组的散度为:0.256
下面是对kl散度的变形,我直接截图了:

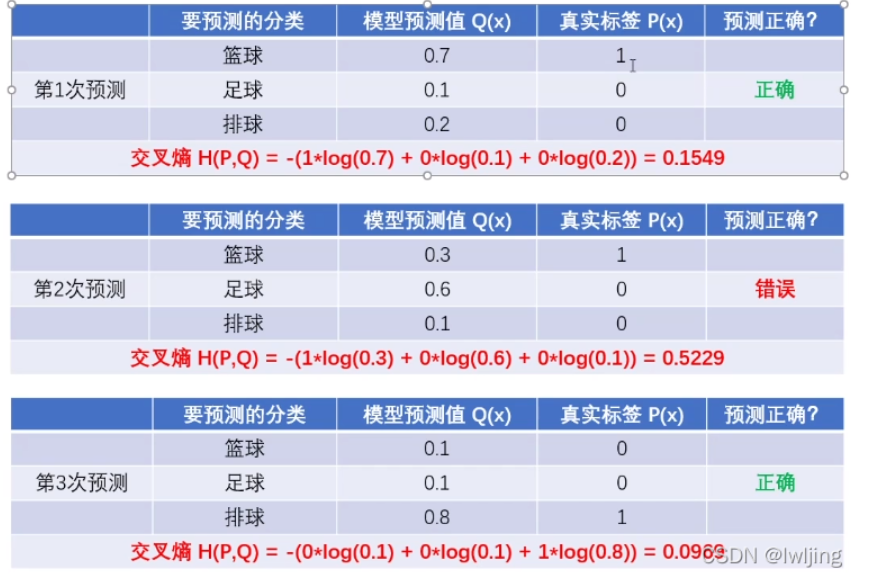
交叉熵
主要应用与度量同一个随机变量X的预测分布Q与真实分布P之间的差距。
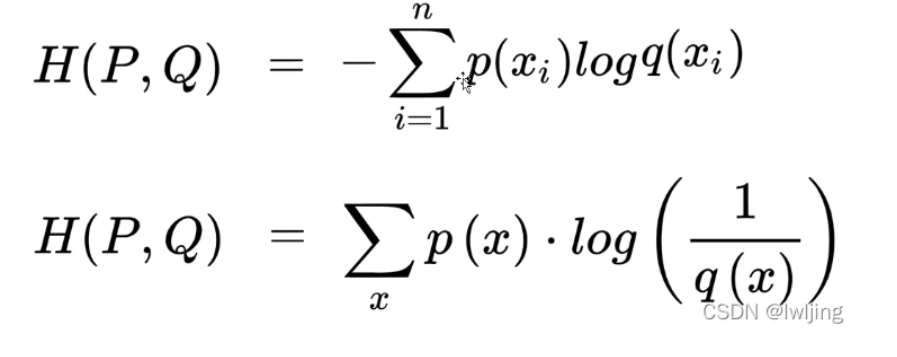

参考1:https://blog.csdn.net/weixin_36815313/article/details/105455056
参考2:https://blog.csdn.net/lwljing/article/details/124139314


 浙公网安备 33010602011771号
浙公网安备 33010602011771号