做题记录(Dec.)
12.2
P14636(NOIP T2)
补一下 NOIP T2。
首先观察样例加推一推我们会发现题中人物的贪心不对的情况只有一种,他选了一个 \(w=1\) 的原价 \(a_i\) 的物品,然后在选 \(w=2\) 的原价为 \(a_k\) 的时候只剩 \(1\) 元,只能选 \(w=1\) 的 \(a_j\),然后发现 \(a_i + a_j < a_k\)。
我们考虑在选 \(i,k\) 之前,已经选了 \(x\) 个 \(w=1\) 和 \(y\) 个 \(w=2\) 的情况,则根据上面的判断,有 \(x+2y=m-2\),剩下的两块钱肯定是用来买 \(i,j\) 的。那么我们可以画出这样一条数轴。
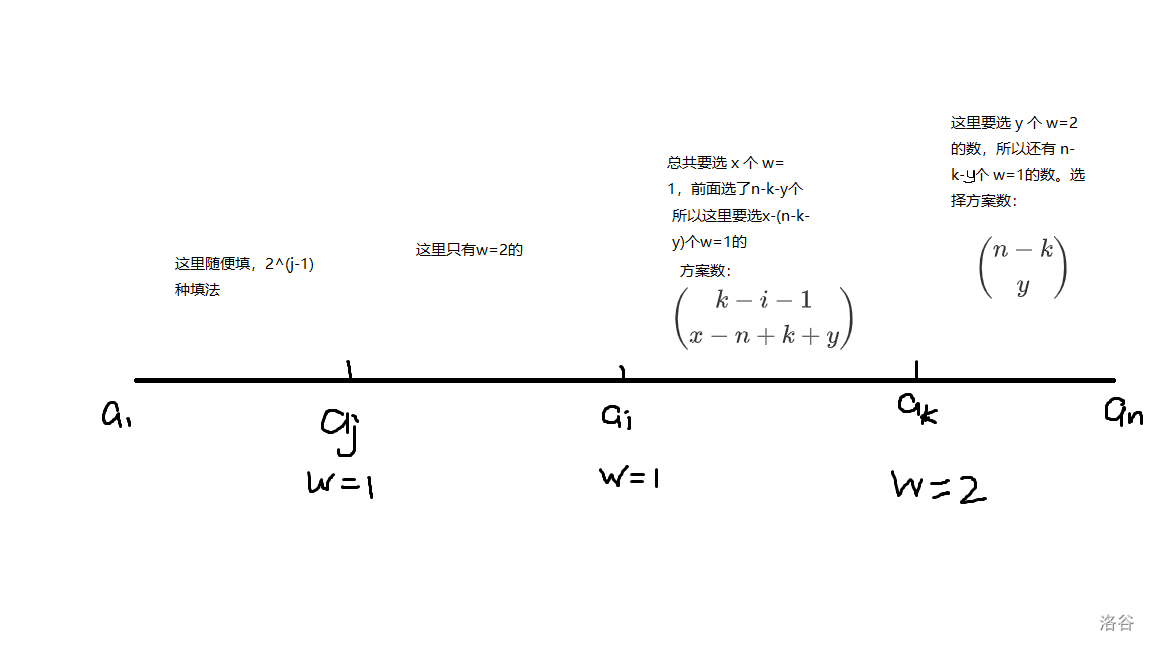
我们可已发现我们枚举的变量有 \(i,j,k,x,y\),答案为
\(x,y\) 有等式关系,所以可以化简为
通过范德蒙德卷积(没错就是上次 ABC 那个),我们发现简化后的式子只需要枚举 \(i,j,k\) 了。
但是 \(n^3\) 过不了,所以我们可以只枚举 \(i,k\),这样 \(j\) 的范围就确定了,可以用双指针做到 \(n^2\)。
复习以前打的板题,准备进入数据结构学习。
12.4
P3919
之前没有写过主席树板子 1。。。
P3834
重温,终于写的像人一点了。
12.5
P3402
可持久化并查集的板子。
其实就是在按秩合并的并查集中,对 \(f\) 和 \(siz\) 的修改都是单点的,放到主席树上就行。
第一次练习写封装。
P2633
重温。
12.6
P3168
感觉主席树板子和这道题的关系等于树状数组两个板子之间的关系。
把单点改区间查改成区间改单点差,差分一下就行。
AT_abc435_e
动态开点线段树板子。和一位?
AT_abc435_f
发现猫猫只会走到在当前点的左边最高点或右边最高点,然后就是一个递归的结构,二叉树,dfs 一下往左或往右,取最大值。
12.14
期中考完回归了。
SP11470
主席树,但是新版本是区间修改区间查。修改标记永久化,查询照常查,记得加上每个点的标记。
12.15
AT_abc255_h*
调了半天加 1h,题解。
12.16
AT_abc256_h*
和上帝造题的七分钟有异曲同工之妙。对于除法向下取整,暴力在线段树上找区间,当区间里的值都相等时可以直接更新。
虽然这样找区间显然很不符合线段树的复杂度,但是每次至少除以二,所以更新次数在没有操作二时也是有上限的,而操作二感性理解一下,改的区间大那么这个大区间下次就可以一起更新,改的区间小那么受影响的节点就不会多。
12.18
CF1326E
线段树。
由于答案单调不增,考虑用一个指针枚举当前答案。
我们发现如果这个答案不会被炸掉,那么在数组中必定存在一个位置 后面的炸弹数 \(p\) 小于等于 后面大于等于 \(x\) 的数的个数 \(q\)。
由于指针枚举到这里,大于等于 \(x\) 的数都炸了,所以肯定炸不到 \(x\)。否则,指针往前走,直到满足条件。
线段树维护每个位置的 \(p-q\),加入炸弹时前缀全减一,答案变小时当前答案的位置前缀全加一。
12.20
P12747
数据结构打久了,确保自己还有脑子。
一个数组记录以当前节点为一个端点,往一个儿子走,走出一条路径,这条路径需要的最多路障数。
对于每个点,递归每个儿子,然后把这个儿子记录的答案和自己现在的答案拼起来更新总答案,再用这个儿子的答案加上这个点更新这个点的答案。没有遍历儿子时答案为这个点的度数(这个点自己为一条路),但这个不能用于更新答案,因为起点和终点不能一样。
12.25
CF702F*
把问题转换一下:把衣服排好序,然后拿每件衣服去更新每个人剩的钱。用平衡树维护剩余钱多少的顺序,每次把树分裂成三个。
第一个的值域是 \([0,c)\),买不起不管,第二个是 \([c,2c)\),这个因为全体要减 \(c\),减完了会和前面的混到一起,所以要把每一个点拿出来重新插入(可以在第一棵树和第三棵树合并后插入),第三棵树是 \([2c,+\infty)\),这棵树减完 \(c\) 还是整体在前两棵树(处理完)后面,所以可以直接 merge。
也算作是复习平衡树并进阶一下。
12.27
CF266E
说实话,我不太会推式子。看看题解得了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号