【瞎总结】组合模型及其组合意义的阐释

【总结】组合模型及其组合意义的阐释

重要说明：本文统一使用"球和格子"模型阐释组合意义。

> (这种东西)极具启发性，有助于人们深刻理解组合数学。——卢华明

名字都是我强行取的，不必在意。

目录

• 【总结】组合模型及其组合意义的阐释
  • 可重组合
    • 描述
    • 公式
    • 组合阐释1(构造法)
    • 组合阐释2(一一对应法)
    • 拓展套路1
    • 拓展套路2
      • 解法1
      • 解法2
    • 拓展套路3
    • 拓展套路4(真的拓展)
    • 拓展套路5(画蛇添足)
  • 不相邻组合
    • 描述
    • 公式
    • 组合阐释1
    • 拓展套路1
  • 格路模型
    • 组合阐释1
    • 组合阐释2
  • 艾提艾斯提模型
    • 组合阐释1(格路)
  • 备胎模型
    • 组合阐释1
    • 扩展套路1
  • 奇偶模型
    • 直接证明1
    • 组合阐释1
  • 黑白模型（范德蒙德卷积)
    • 组合阐释1
    • 拓展套路
  • 下定上动
    • 组合阐释1
  • 下动上定
    • 直接证明1
    • 组合阐释1
  • 【小结】\(n\)球\(m\)盒：盒子区别？球区别？空盒？
    • 定义1
    • 证明1:无区别 无区别 有空盒
    • 证明2:无区别 无区别 无空盒
  • 错排问题
    • 描述
    • 递推公式
    • 求通项(指数型生成函数)
    • 求通项(组合阐释)
  • 分圆排列(第一类斯特林)
    • 描述
    • 递推关系
    • 组合阐释1
    • 扩展套路1
  • 子集列(第二类斯特林数)
    • 描述
    • 递推关系
    • 容斥关系
  • 反演关系
    • 特殊值和性质
      • • 弦鸽不缀

可重组合

描述

有\(m\)种球每种球都是足够多的，有\(n\)个盒子，现在要把盒子塞满(一种球可以用多次)，多少种方案？

公式

\[f_0(n,m)={{m+n-1}\choose n} \]

组合阐释1(构造法)

不失一般性，把球编号，然后按照从小往大排序，设第\(i\)位置上面为\(a_i\)，构造一个新的数列\(b_i=a_i+i\)，很显然\(b_i\)是互不相同的。我们知道\(b_i \in [1+1,n+m]\)的，所以问题就变成了从\([2,n+m]\)中选出\(n\)个数，显然这个的方案数就是\(\begin{pmatrix}m+n-1\\n\end{pmatrix}\) 个。

组合阐释2(一一对应法)

从2到\(m+n\)任意选出\(n\)个数，即\(\begin{pmatrix}m+n-1\\n\end{pmatrix}\)方法，这些取的方法和可重组合的方法一一对应。具体对应方式是对于取出来的第\(i\)小数减去\(i\)，这样得出来的新数列的范围就在\([1,m]\)的范围内，并且新数列会有相同的元素，对应的就是选了几个相同元素。

拓展套路1

盒子有编号怎么办？

\[f_1(n,m)= A_{m+n-1}^{n}={{m+n-1}\choose n}\times n! \]

之前的盒子是没有编号的，现在的盒子有编号了，之前每一种无序的安排都可以对应到\(n!\)个有序安排内。

拓展套路2

盒子可以不放满怎么办？

解法1

\[f_2(n,m)=\sum_{i=1}^{n}{n\choose i}{f_0(m,i)} \]

过于显然不解释。

解法2

相当于多了一个球，我们把这个球叫做"无球"，选择这个球代表盒子是空的。所以：

\[f_2(n,m)=f_0(n+1,m) \]

这就给了我们一个可重组合的递推公式(滑稽)

拓展套路3

球有个数限制怎么办？

\(O(2^n)\)容斥。

\[f_3(n,m)=\sum_{s \subseteq S} (-1)^{|s|}f_2(n+1,m-\sum_{i\in s}(a_i+1)) \]

相当于钦定一些球至少选择\(a_i+1\)个使得它们一定选多了，然后容斥原理即可。

拓展套路4(真的拓展)

要求这些某种球只能选择它给定集合\(S_i\)内的数怎么办？

\[\prod_{i=1}^{m}\sum_{j\in S_i}x^j \]

的\(n\)项系数

拓展套路5(画蛇添足)

我想算复杂一点怎么办？

\[\prod_{i=1}^{m}\sum_{j=1}^{\inf}x^j=(\frac{x}{1-x})^m \]

的\(n\)项系数...

其实可以用来多项式优化。

不相邻组合

描述

有\(n\)个球，\(m\)个盒子，(注意看，这里和之前的表述不同了)选出的球不能相邻，有多少种组合方式？

公式

\[f_0(n,m)={{n-m+1}\choose{m}} \]

组合阐释1

从\([0,n-m]\)中选出\(m\)个数，将第\(i\)小的数加上\(i\)构成新的序列，新的序列在\([1,n]\)的范围内，并且不会重复。

拓展套路1

可重不相邻组合？

我不太会\(O(1)\)，貌似会\(O(n)\)

\[\sum_{i=1}^n{n-i+1\choose i}{i+m-1\choose m} \]

就这么过掉了，毕竟不知道什么..

格路模型

从坐标原点走到\((n,m)\)的方案数是

\[{{n+m}\choose n} \]

组合阐释1

从原点走到\((n,m)\)一定要走\(n+m\)步，从\(n+m\)次走步(大雾)中选出\(n\)步往x正方向走就对应了每一种走路的方法。

比yyb在NOIP集训专题分享上在讲台上讲的好多了

组合阐释2

设\(dp(i,j)\)表示从原点走到\((i,j)\)的方案:根据加法原理

\[dp(i,j)=dp(i-1,j)+dp(i,j-1) \]

而由组合数递推公式

\[{{m+n}\choose n}={{m+n-1}\choose n-1}+{{m+n-1}\choose n} \]

记\(f(n,m)={{m+n}\choose n}\)

则有

\[f(n,m)=f(n-1,m)+f(n,m-1) \]

和上上式一样。

格路是我们重要的思维方式，也是重要的证(gan xing)明(li jie)方式。

艾提艾斯提模型

别看这个名字

等式:

\[{{n+m+1}\choose m}={{n+m}\choose m}+\sum_{i=1}^m {n+m-i\choose m-i} \]

组合阐释1(格路)

\(\begin{pmatrix} n+m+1\\m\end{pmatrix}\):从原点到\((n+1,m)\)的方案数

\(\begin{pmatrix} n+m \\ m \end{pmatrix}\):从原点到到\((n,m)\)的方案数

\(\begin{pmatrix} n+m-i \\ m-i \end{pmatrix}\):从原点到\((n,m-i)\)的方案数

又因为，从原点到\((n+1,m)\)的路径方案数是这样构成的

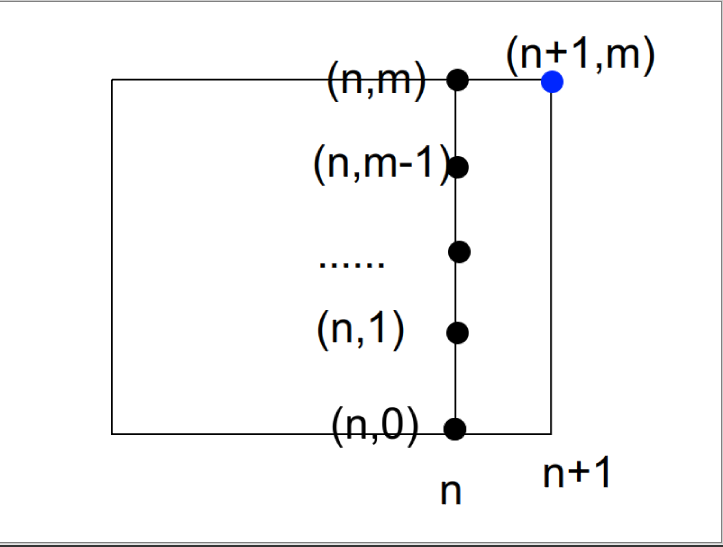
蓝色到蓝色点的路径显然由所有黑色点贡献

所以就证完了。

备胎模型

考虑一个这样的恒式子

\[{n \choose l}{l \choose r}={n \choose r}{n-r\choose l-r},l\in[r,n] \]

组合阐释1

考虑从\(n\)选出\(l\)个再从\(l\)选出\(r\)个和直接$\begin{pmatrix} n \ r \end{pmatrix} $有什么区别？？

当然是有的，因为有\(n-r\)个你选出来的最后没要...

所以选出这\(n-r\)个炮灰也是会造成方案的不同啊

所以上面这个式子的组合意义就很清晰了

扩展套路1

多选几轮？

\[{n \choose l}{r\choose q}{q\choose m}={n-q\choose l-q}{n-m\choose q-m}{n \choose q} \]

找规律大法好 \((n=a_0)\)

\[\prod_{i=1}^k{a_{i-1}\choose a_i}={a_0\choose a_k}\prod_{i=1}^{k-1}{a_0-a_i\choose a_i- a_{i+1}} \]

奇偶模型

\[\sum_{i=0} ^n(-1)^i{n \choose i}=[n=0] \]

注意到上式也说明了对于\((-1)^{i+1}\)也是成立的。

直接证明1

\[(x+y)^n= \sum_{i=0}^n {n \choose i}x^iy^{n-i} \]

令\(x=1,y=-1\)证毕。

(没有营养的)

组合阐释1

上式相当于不停从\(n\)中选个子集出来(包括空集)，然后把所有集合的大小为偶数的方案加起来，把所有集合的大小为奇数的方案加起来，然后相减。

所以我们只要建立起一个奇子集和分成偶子集的各种方案之间建立一个一一对应的关系就好了。

一一对应很显然吧...

分析随便某个元素\(x\)，它只有两种状态:在分出来的子集内，不在分出来的子集内。对于一个任何一个给定的集合，我们就直接把\(x\)是否存在的这个布尔条件!一下，然后就改变了这个集合的奇偶性，而且新增的方案也是合法的。这样就一一对应起来了。

黑白模型（范德蒙德卷积)

考虑恒等式

\[{m+n\choose r} =\sum_{i=0}^r {m\choose i}{n\choose r-i}, r\le m \le n \]

组合阐释1

分成\(m\)个黑球和\(n\)个白球，从\(m+n\)个球里选出\(r\)个无外乎从黑球选\(i\)个再从白球中选\(r-i\)个。

拓展套路

一个形式漂亮的式子

\[\sum_{i=0}^n{n\choose i}^2={2n\choose n} \]

令\(m=n=r\)，并且代入\(\begin{pmatrix}a+b\\a\end{pmatrix}=\begin{pmatrix}a+b\\b\end{pmatrix}\)即可。

下定上动

考虑恒等式

\[\sum_{i=r}^n{i \choose r}={n+1\choose r+1} \]

组合阐释1

等式左边相当于盒子不变，而球从\(n\)变到\(r\)，也就是说，选择球的范围变小了。

这也就是说，供我们选择球的个数的范围为\([r,n]\)。

考虑等式右边，我们把球编号，并且我们令选出来的编号最大的球的编号为\(k\)，那么\(k-1\in[r,n]\)，而其他选择出来的球的编号大小一定\(\le k-1\le r\)，也就是相当于在\([1,k-1]\)中任选\(r\)个，而\(k-1\in[r,n]\)，所以此时右边的组合一样和左边一样了。

下动上定

那么上定下动呢？

就是二项式定理，傻瓜

\[\sum_{i=1}^n {n\choose i}=2^n \]

直接证明1

\[(1+1)^n= \sum_{i=0}^n {n \choose i}1^i1^{n-i} \]

组合阐释1

左边相当于给一个\(n\)个元素的集合取子集。

所以取子集的方案数是什么？显然可以一个元素一个元素地考虑，只考虑一个元素在不在选出的集合内，这样的话对于每个元素只有\(2\)种选择，那么总共\(n\)个元素的话就是\(2^n\)种选择。

【小结】\(n\)球\(m\)盒：盒子区别？球区别？空盒？

• \(n\)个球 \(m\)个盒子 是否空盒 方案数

• 有区别 有区别 有空盒 \(m^n\)

• 有区别 有区别 无空盒 \(m!{\begin{Bmatrix}n \\ \\m\end{Bmatrix}}\) ，不考虑盒子区别时有\({\begin{Bmatrix}n \\ \\m\end{Bmatrix}}\)种，再乘上\(m!\)。定义在下

• 有区别 无区别 有空盒 \(\sum_i^{\min\{n,m\}} {\begin{Bmatrix}n \\ \\i\end{Bmatrix}}\) ，枚举多少个盒子有，再斯特林数。

• 有区别 无区别 无空盒 \({\begin{Bmatrix}n \\ \\m\end{Bmatrix}}\)，套公式

• 无区别 有区别 有空盒 \(\text{可重组合}(n,m)=\begin{pmatrix}n+m-1\\ n \end{pmatrix}\)

• 无区别 有区别 无空盒 \({\begin{pmatrix}n-1 \\ \\ m-1\end{pmatrix}}\)把球排成一列，然后插在\(n-1\)空里插\(m-1\)个。

• 无区别 无区别 有空盒 \(G(x)=\dfrac 1 {(1-x)(1-x^2)\dots(1-x^{m-1})(1-x^m)}\)的\(x^n\)系数

• 无区别 无区别 无空盒 \(G(x)=\dfrac 1 {(1-x)(1-x^2)\dots(1-x^{m-1})(1-x^m)}\)的\(x^{n-m}\)系数

注：可能不是最优的解法，欢迎交流

定义1

\[\begin{Bmatrix} n \\ \\ m \end{Bmatrix} \]

第二类斯特林数，表示将\(n\)个有区别的球放到\(m\)个无区别的盒子，盒子不为空。或者说\(n\)个元素分为\(m\)个非空集合。

计算方式

\[\begin{Bmatrix} n \\ \\ m \end{Bmatrix}=\frac 1 {m!}\sum_{i=0}^{m-1} (-1)^i{m \choose i}{(m-i)^n} \]

右边相当于先让盒子可以为空，然后容斥，每次枚举有多少个盒子是空的即可。

证明1:无区别 无区别 有空盒

• 无区别 无区别 有空盒 \(G(x)=\dfrac 1 {(1-x)(1-x^2)\dots(1-x^{m-1})(1-x^m)}\)的\(x^n\)系数。

这个问题就相当于盒子选球，方案有区别当且仅当存在不同数目的某大小的集合，所以就是这样

\[G(x)=(1+x+x^2+\dots)(1+x^2+x^4+\dots)(1+x^3+x^6+\dots)\dots(1+x^m+x^{2m}+\dots) \]

答案就是\(x^n\)系数，代表由这些盒子中的球组成了\(n\)个球。

母函数简化一下

\[G(x)={\dfrac {1} {1-x} }{\dfrac {1} {1-x^2} }{\dfrac {1} {1-x^3} }\dots{\dfrac {1} {1-x^m} } \]

证明2:无区别 无区别 无空盒

先钦定每个盒子里放一个球，再随便选。化为\(n-m\)个球的有空盒的问题。

\[G(x)={\dfrac {1} {1-x} }{\dfrac {1} {1-x^2} }{\dfrac {1} {1-x^3} }\dots{\dfrac {1} {1-x^m} } \]

的\(x^{n-m}\)系数。

错排问题

描述

一个排列\(p\)，它的错排\(p'\)的定义是不存在一个位置他们的数相同。

\(D_n\)表示对于排列\(1,2,3,4,5,\dots n\)的错排的个数。

很显然错排个数只和排列长度有关。

递推公式

考虑我们现在有排列

\(1,2,3,\dots n-1,n\)

将\(n\)和1到n-1任何一个数k互换，然后剩下的\(n-1\)个数进行错排。注意到错排个数只和排列长度有关，则有\((n-1)D_{n-1}\)方案。但是我们考虑到k永远不会回到k原来的那个位置(被n占了)，所以还有\(n-1-1=n-2\)个元素进行错排。得到递推

\[D_n=(n-1)(D_{n-1}+D_{n-2}) \]

\(D_0=1,D_1=0\)

当然可以再设一个\(B_n=nD_n\)然后得到递推式

\[D_n=B_{n-1}+B_{n-2}+D_{n-2} \]

然后直接矩阵快速幂\(O(16\log n)\)

求通项(指数型生成函数)

好吧开始必修零点五的(大雾)通项求法吧

\[\begin{array} & D_n-nD_{n-1} \\ &=-[D_{n-1}-(n-1)D_{n-2}] \\ &=(-1)^2[D_{n-2}-(n-2)D_{n-3}] \\ &= \dots \\ &=(-1)^n(D_2-D_1) \\ &=(-1)^n \end{array} \]

构造指数型母函数

\[G(x)=D_0+D_1\dfrac 1 {1!}x+\dfrac 1 {2!}D_2x^2+\dfrac 1 {3!}D_3x^3+\dots \]

根据泰勒展开

\[e^{-x}=\dfrac 1 {0!} -\dfrac 1 {1!} x+\dfrac 1 {2!}x^2-\dfrac 1 {3!}x^3\dots \]

所以有

\[G(x)-xG(x)=e^{-x} \]

整理得

\[\begin{array} &G(x)=\dfrac {e^{-x}} {1-x} \\ =e^{-x}(\dfrac 1 {1-x}) \\ =(\dfrac 1 {0!} -\dfrac 1 {1!} x+\dfrac 1 {2!}x^2-\dfrac 1 {3!}x^3\dots)(1+x+x^2+x^3+\dots) \\ =D_0+D_1\dfrac 1 {1!}x+\dfrac 1 {2!}D_2x^2+\dfrac 1 {3!}D_3x^3+\dots \end{array} \]

比较系数

\[[x^n]=\sum_{i=0}^n(-1)^i\dfrac {n!} {i!}=D_n \]

如果你看不懂我也没办法，推的办法就是根据乘法分配律还有\(\dfrac 1 {a}=b \dfrac 1 {ab}\)

所以

\[D_n=\sum_{i=0}^n (-1)^i\dfrac {n!} {i!} \]

但是！这个式子有组合意义。

求通项(组合阐释)

右边这个式子就相当枚举有多少个位置是不动的，此时的方案数就是\(\dfrac {n!} {i!}\)，然后容斥即可。最后也是得到上面那个式子。

\[D_n=\sum_{i=0}^n (-1)^i\dfrac {n!} {i!} \]

这个问题告诉我们了，组合意义阐释法非常牛逼，吊打各种求通项的方法。

组合意义阐释法非常牛逼，吊打一切求通项的方法。

但是这个式子没什么卵用

分圆排列(第一类斯特林)

描述

\[\begin{bmatrix}n \\ m\end{bmatrix} \]

一个\(n\)个人，分成\(m\)个圆排列

递推关系

\[\begin{bmatrix}n \\ m\end{bmatrix}=\begin{bmatrix}n-1 \\ m-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1 \\ m\end{bmatrix} \\ {\begin{bmatrix}n \\ n\end{bmatrix}=1},{\begin{bmatrix}n \\ 0\end{bmatrix}=0},n>0 \]

组合阐释1

上式的组合意义十分明显，要么自己新开一桌\(\begin{bmatrix}n-1 \\ m-1\end{bmatrix}\)，要么随便坐到一个人的右边\((n-1)\begin{bmatrix}n-1 \\ m\end{bmatrix}\)

扩展套路1

\[\sum_{i=0}^n {\begin{bmatrix} n \\ i\end{bmatrix}}=n! \]

组合意义，右边表示\(n\)个数的排列。

现在我们的任务就是建立左边每个圆排列的方案和真正的排列一一对应。

考虑一个排列，

\[\begin{matrix} a_1&a_2&a_3&a_4&\dots &a_n\end{matrix} \]

我们考虑一直这样做：设\(f(i)=a_i\)，迭代\(k=f(k)\)。

很显然，我们一定会出现循环，因为\(k\)只有\(n\)种取值，至多\(n\)次迭代之后，一定会回到原来的那个\(k\)。

也是很显然，一个排列用这种办法构造，会多个这样的循环，这种循环的个数可以对应上几个桌子。举个例子

\[P=\begin{bmatrix}1,2,4,3,6,5\end{bmatrix} \]

它就对应了以下轮换：

\[\S =\begin{Bmatrix} [1]&[2]&[3,4]&[5,6] \end{Bmatrix} \]

对应一个分圆排列。

我们现在就证明了一个排列可以对应上一个轮换排列。类似的方法可以证明一个轮换可以反过来对应这一个排列。我们现在就把排列和轮换排列一一对应了。

实际上...上述说明方法运用了置换群的思想。没错你已经会群论了\(\sqrt {\quad}\)

子集列(第二类斯特林数)

描述

将\(n\)个有区别的球放入\(m\)个无区别的盒子，盒子非空。上面那个小结里就介绍了第一类斯特林数。

\[\begin{Bmatrix}n\\ \\ m\end{Bmatrix} \]

或者换一个说法，\(m\)个元素，可重地组合为\(n\)个整体，要求每个元素都被选到。

递推关系

\[\begin{Bmatrix}n\\ \\ m\end{Bmatrix}=\begin{Bmatrix}n-1\\ \\ m-1\end{Bmatrix}+m\begin{Bmatrix}n-1\\ \\ m\end{Bmatrix} \]

组合一样非常明显，要么自己新建一个集合，要么随便加入某个已有的集合中。

容斥关系

\[\begin{Bmatrix}n\\ \\ m\end{Bmatrix}=\dfrac 1 {m!} \sum_{i=0}^{m-1}(-1)^i{m\choose i}(m-i)^n \]

不再赘述。

反演关系

\[i^k=\sum_{j=0}^{\min\{i,k\}} {k\brace j}\begin{pmatrix} i \\j\end{pmatrix}j! \]

证明在这里！【总结】容斥原理与反演

特殊值和性质

• \(\begin{Bmatrix}n\\ \\ 2\end{Bmatrix}=2^n-1,n>0\)

• \(\begin{Bmatrix}n\\ \\ 3\end{Bmatrix}=\dfrac 1 {3!}(3^n-3\times 2^n+3)=\dfrac {3^{n-1}+1-2^n} {2}\)

• \(\begin{Bmatrix}n\\ \\ n-1\end{Bmatrix}=\begin{pmatrix}n\\ \\ 2\end{pmatrix}\)

• \(\begin{Bmatrix}n\\ \\ n-2\end{Bmatrix}=\begin{pmatrix}n\\ \\ 3\end{pmatrix}+3\begin{pmatrix}n\\ \\ 4\end{pmatrix}\)

---

(鸡贼口中的)超级卡特兰数
欧拉数
调和数
伯努利数

还有些自己也不会。To be continued...

弦鸽不缀