概率论

概率论

参考资料

OI-Wiki

概率基础知识

普通概率基础

\(P(A)\) 表示事件集合 \(A\) 发生的概率。

\(P(A+B)\) 表示事件集合 $A \cup B $ 发生的概率（即 \(A\) 或 \(B\) 发生）

\(P(A-B)\) 表示事件集合 \(A\) 发生，事件 \(B\) 不发生的概率。

\(P(AB)\) 表示事件集合 \(A,B\) 都发生的概率。

容斥原理：

\(P(A+B) = P(A) + P(B) - P(AB)\\ P(A-B) = P(A) - P(AB)\)

---

条件概率基础

\(P(B|A)\) 表示在 \(A\) 已经发生的前提下，\(B\) 发生的概率。

\(P(B|A) = \frac{P(AB)}{P(A)}\)

---

Bayes 公式

为什么 OI 题要学遗传学啊/ll，我们以一个简单的遗传问题为例理解一下 Bayes 公式。

母亲基因型是 \(AA,Aa,aa\) 的概率分别是 \(P(A_1),P(A_2),P(A_3)\)，父亲基因型是 \(AA,Aa,aa\) 的概率分别是 \(P(B_1),P(B_2),P(B_3)\)。（均为生孩子前）

现在他们生了一个孩子，患有隐性遗传病，即 \(P(C_3) = 1\)。求在此条件下的 \(P(A_*),P(B_*)\)。

\[P(A_3 | C_3) = \frac{P(A_3C_3)}{P(C_3)} = \frac{P(A_3)P(C_3|A_3)}{P(A_1)P(C_3|A_1) + P(A_2)P(C_3|A_2) + P(A_3)P(C_3|A_3)} \]

我们已知 \(P(A_*),P(C_3)\)。\(P(C_3|A_i) = \sum_j P(C_3|A_iB_j)\)，也是已知的。

所以可以求出 \(P(A_3|C_3)\) 了。

---

独立事件

对于独立的事件，满足

\(P(AB) = P(A)P(B)\)。

期望

期望基础

主要讨论离散型随机变量的期望。

\(E(X)\) 表示变量 \(X\) 的期望值。

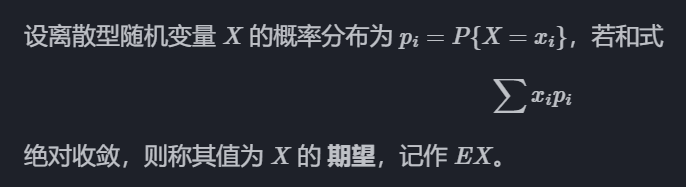
就是所有情况的数值乘概率之和。

---

期望的性质

线性性：

\(E(aX+b) = a \cdot E(x)+b\\ E(X+Y) = E(X) + E(Y)\)

\(E(XY) = E(X) \cdot E(Y)\)（\(X,Y\) 为独立变量）

条件期望的全期望公式：

\(E(E(X|Y)) = E(X)\)

即先对 \(X\) 在给定 \(Y\) 下求期望，再对 \(Y\) 求期望，结果等同于直接对 \(X\) 求期望。

概率 DP

一般情况下，解决概率问题需要顺序循环，而解决期望问题使用逆序循环，如果定义的状态转移方程存在后效性问题，还需要用到高斯消元来优化。概率 DP 也会结合其他知识进行考察，例如状态压缩，树上进行 DP 转移等。——OI-Wiki

---

一般我们画出转移的有向图，然后从终态推到初态。

期望 DP 的转移方程大多是下面这样的类型：

\[f_u = \sum_{v\in son_u} p_v (f_v+1) \]

---

期望 期望 DP。转化成有向图随机游走，由终态推至初态的期望值。

这题的期望转移有向图是这样的：

所以转移方程就是 \(f_i = p_{i+1} f_{i+1} + (1-p{i+1}) f_0 + 1\)

---

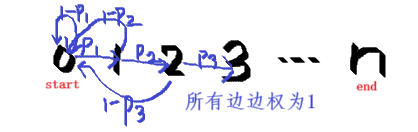
航行 难一点的期望 DP。转化成有向图随机游走，由终态推至初态的期望值。

因为我们只关心 \(f_{\cdot,0}\) 的值，所以可以在 \(f_{\cdot,0}\) 之间转移。预处理出它们是怎么转移的（转移概率和边权）。

从 \(f_{i,0}\) 第一次到 \(f_{\cdot,0}\) 期间，船一定是往同一方向行驶的。因此期间所有 \(f_{x,v}\) 都满足 \(x>i \land v \ge 0\) 或 \(x<i \land v \le 0\)。这里的转移是无环的。预处理的期望 DP 有向图见下图。要求的是从 \((i,0)\) 到 \((j,0)\) 的概率 \(P\) 和期望边权 \(W\)。

给出期望转移的一条式子（这里 \(f_{i,v}\) 表示从 \((s,0)\) 到 \((i,v)\) 在确定到达的条件下的期望时间，而原题解代码定义的应该是乘上了到达的概率的值）：

\(f_{i,v} = \sum_{j+v = i} p_j (f_{j,v-1}+1)\)

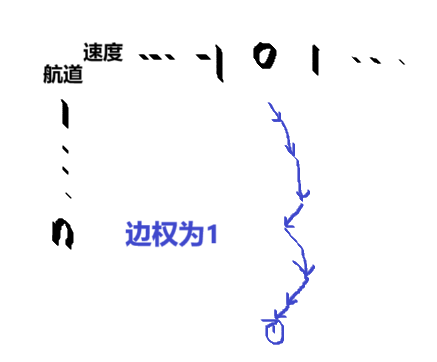
然后再画一个 \(f_{\cdot,0}\) 之间的期望 DP 转移有向图。边的概率和期望是预处理求得的值。

那么 \((s,0) \to (i,0)\) 的期望时间就是：

\(E_{s,0} = \sum_{(s,0) 可以到达 (i,0)} E_{i,0} P_{(s,0) \to (i,0)} + W_{(s,0) \to (i,0)} P_{(s,0) \to (i,0)}\)

---

P5104 红包发红包

第一个人期望抢到 \(E(1)=\frac{w}{2}\) 元，那么第二个人期望抢到期望剩下的钱数量的一般，即 \(E(2) = \frac{w-E(1)}{2}\) 元。那么第 \(k\) 个人期望抢到 \(\frac{w}{2^k}\) 元。

为什么 E(2) 可以这样求（较为严谨的证明）

\[\begin{aligned} E(1) & = \frac{\int_0^w x \text{d}x}{w} = \frac{w}{2}\\ E(Y|X) & = \cdots = \frac{w-X}2 \text{（X表示第一个人抢到的钱数，Y表示第二个人抢到的钱数）}\\ E(2) & = E(Y) = E(E(Y|X)) = E(\frac{w-X}2) = \frac{w-E(1)}2\\ \end{aligned} \]

---