云剪贴板

结论：假完了。

虽然可以改，但是洛谷题解做法更简洁。

但是可以把换根 DP 改成求直径吧。

做法

求求大神帮忙 hack t3/kel，真没招了/kel

下面是做法：

代码

#include<bits/stdc++.h>
#define sf scanf 
#define pf printf 
#define rep(x,y,z) for(int x=y;x<=z;x++) 
#define per(x,y,z) for(int x=y;x>=z;x--) 
using namespace std;
typedef long long ll;
namespace wing_heart {
	constexpr int N=1e5+7;
	int T,n;
	int h,t,len;
	vector<int> to[N];
	int dep[N],st1[N],st2[N];
	int *toh,*tot;
	void re() { swap(h,t), swap(toh,tot); }
	void dfs0(int u,int fa) {
		toh[u]=fa;
		for(int v : to[u]) if(v^fa) {
			dfs0(v,u);
		}
	}
	void build_tot() { 
		int x=t; 
		while(x!=h) tot[toh[x]]=x, x=toh[x]; 
	}
	int dfs(int u,int fa) {
		dep[u]=dep[fa]+1;
		toh[u]=0;
		int mx=dep[u];
		for(int v : to[u]) if(v^fa) {
			int tmp = dfs(v,u);
			if(tmp>mx) mx=tmp, toh[u]=v;
		}
		return mx;
	}
	void run() {
		dep[tot[h]]=0;
		dfs(h,tot[h]);
		while(toh[h]) h=toh[h],t=toh[t];
		build_tot();
		// pf("%d %d\n",h,t); fflush(stdout);
	}
	void getlen() {
		len=1;
		int x=t;
		while(x!=h) ++len, x=toh[x];
		// pf("len = %d\n",len);
	}
	int mxdep[N];
	bool check(int u,int fa) {
		dep[u]=dep[fa]+1;
		mxdep[u]=dep[u];
		int cnt=0;
		for(int v : to[u]) if(v^fa) {
			if(check(v,u)) return 1;
			mxdep[u]=max(mxdep[u],mxdep[v]);
			if(mxdep[v]-dep[u]+1>=len) ++cnt;
		}
		// pf("%d %d %d\n",u,fa,mxdep[u]);
		if(cnt>=2) return 1;
		return 0;
	}
	void main() {
		sf("%d",&T);
		// int line=0;
		while(T--) {
			sf("%d%d%d",&n,&h,&t);
			// pf("line %d\n",line+1);
			// line+=n;
			rep(i,1,n) to[i].clear();
			toh=st1,tot=st2;
			rep(i,1,n-1) {
				int u,v;
				sf("%d%d",&u,&v);
				to[u].push_back(v), to[v].push_back(u);
			}
			// assert(dep[0]==0);
			dfs0(h,0);
			build_tot();
			run();
			re();
			run();
			re();
			run();
			// 走到直径上
			getlen();
			dep[toh[t]]=0;
			if(check(t,toh[t])) puts("YES");
			else puts("NO");
		}
	}
}
int main() {
	#ifdef LOCAL 
	// freopen("in.txt","r",stdin);
	freopen("my.out","w",stdout);
	#else  
	freopen("inverse.in","r",stdin);
	freopen("inverse.out","w",stdout);
	#endif 
	wing_heart :: main();
}

第一个出错的数据（模拟赛题数据）

http://cplusoj.com/d/senior/record/6916a972cd056b0e09db9484

3-7，有 $4$ 个错点，均是应输出 YES。其中第一个出错位置在 in 的第 12264 行，out 的 44 行。下面的数据就是这个位置截出来的。

3-8 没错。

CF 上 WA on #2。输出的前 100 行里，只有第 43 行出错。也是应输出 YES。https://codeforces.com/contest/1381/submission/348842167

应当输出 YES。

提供对拍代码

我拍了很多 $n=16,n=30,n=100$，没拍出来/ll

Linux 版。

shuju.cpp

#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
namespace wing_heart {
	int n=16;
	mt19937 rd(random_device{}());
	int rand(int l,int r) { return rd()%(r-l+1)+l; }
	void main() {
		puts("1");
		int x=rand(1,n);
		int y=rand(1,n);
		while(x==y) y=rand(1,n);
		pf("%d %d %d\n",n,x,y);
		rep(i,2,n) {
			int fa=rand(1,i-1);
			pf("%d %d\n",fa,i);
		}
	}
}
int main() {
	freopen("in.txt","w",stdout);
	wing_heart :: main();
}

checker.cpp

std 需要关闭文件读写。

#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
int main() {
	while(1) {
		system("./shuju");
		system("./inverse < in.txt");
		system("./std < in.txt > std.out");
		if(system("diff my.out std.out")) {
			puts("WA");
			exit(0);
		} else puts("AC");
	}
}

题目菱形一种情况证明

要证明这种情况为什么可以转化成别的情况，而不是需要 $5$ 个点。

考虑对菱形进行不劣的变换。

当菱形越来越像正方形时，它的边长会变短。

这是一种情况（情况 A）（因为有一个点可以到顶点，所以 $3$ 个点可以确定出菱形）：

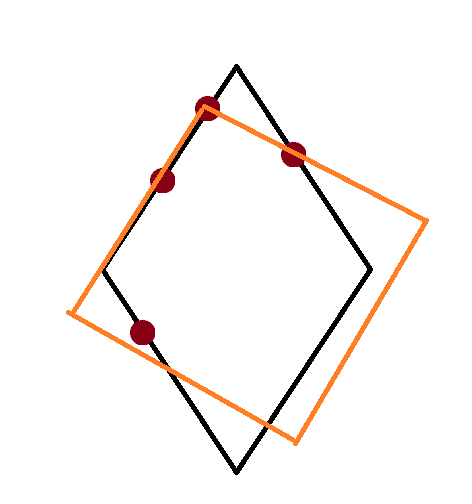
假如有一个蓝色的点，就会变成下面这种情况 B：

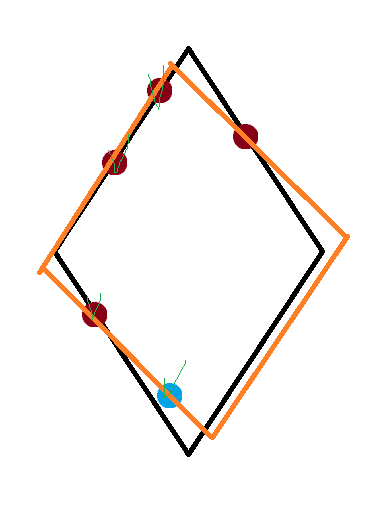
如果向远离正方向的方向对菱形进行变换，会有：

下面这个也是情况 A，同理，如果有一个蓝点卡住就会变成情况 B。

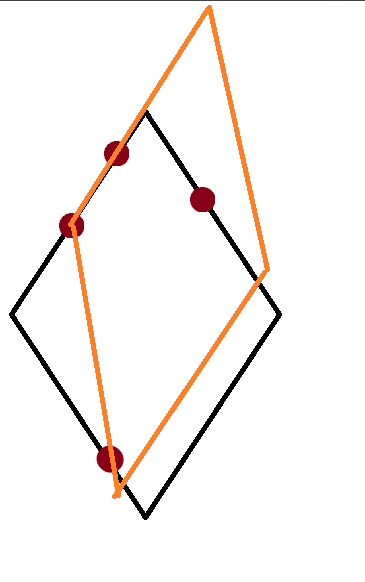
下面是情况 C：

唉，要是变换的时候有一个红色点出去了怎么办？

比如这种，左下角的红点出去了是因为它的位置太下了。边长又缩短了，它就出去了。

可以把菱形往远离正方形的方向（即边长变长）变换，变成上面的情况，左下角的红点一定会被变换后的菱形严格包含。

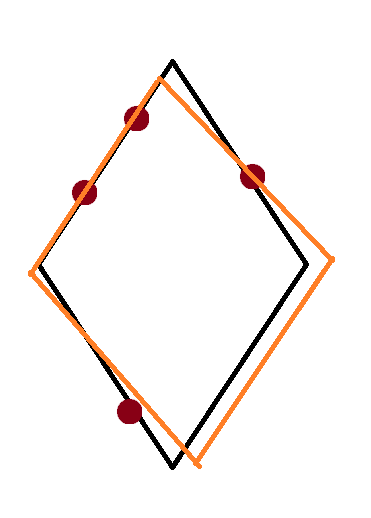
还有一些其他的情况，感觉无法全部列完，比如下面这种：

似乎可以总结成两种情况，分别向远离正方形和靠近正方向两个方向变换。变换直到某条边被一个点卡住为止。下图演示的是被新的蓝色点卡住的情况（蓝色点未标出）：

至此证明了这一种情况一定会被别的情况搜到。

我们其实是要找一种枚举若干点的方案，使得《若干点》可以确定出唯一的菱形，且所有有用的点集都会被搜到。

考虑一个点集，找出它的凸包。（黑色是点集的凸包）

显然点集被菱形包含完全等价于凸包被菱形包含。

假设存在一个合法的红色菱形，这个菱形与凸包可能有若干个交点，如下图这种情况：

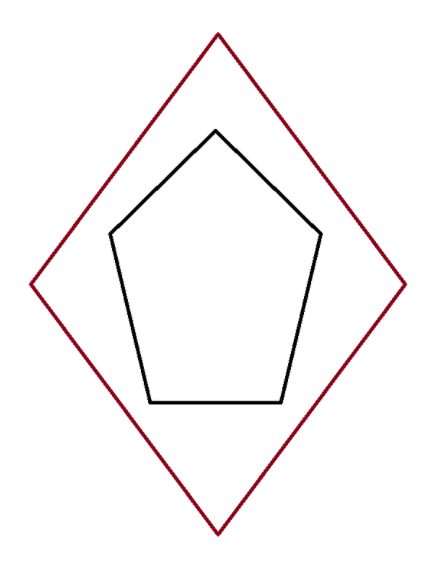
显然可以先把一个黑边贴着菱形（平移）：

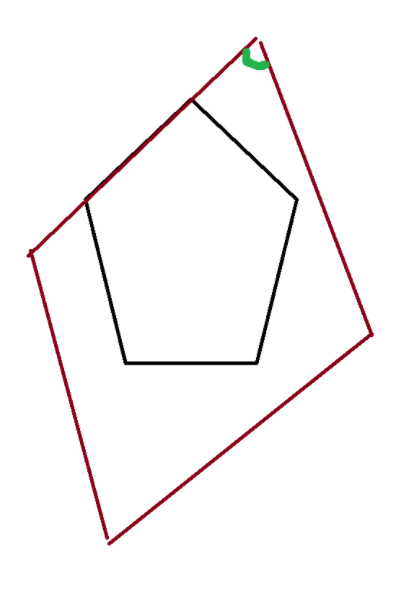
然后把上面绿色的角（顶角）调小（保证面积相同），变成下面的样子。（：

然后把顶角调大，同时向下平移（保证面积相同），直到粉色或者橙色的边碰到凸包：

下图是橙色碰到凸包（情况 A）：

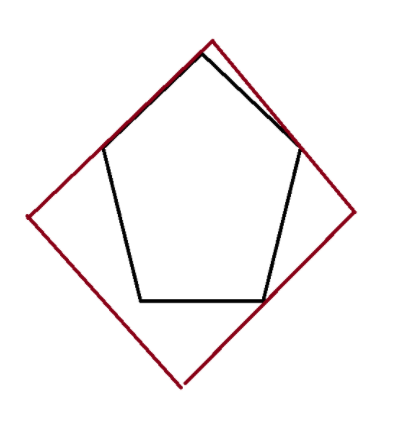
下图数粉色碰到凸包（情况 B）：

下面是顶角开到最大粉色和橙色仍然都碰不到凸包（情况 C）：

显然没有其他情况了。

然后要继续转化情况 B。

平移直到右下边碰到凸包，如下图：

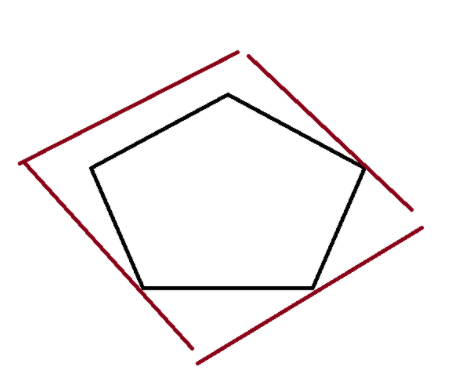
用于测试

欢迎使用 Cmd Markdown 编辑阅读器

二级标题

三级标题

四级标题

五级标题

六级标题

( x^n )

你好！

Windows/Mac/Linux 全平台客户端

你好。

请保留此份 Cmd Markdown 的欢迎稿兼使用说明，如需撰写新稿件，点击顶部工具栏右侧的 新文稿 或者使用快捷键 Ctrl+Alt+N。

行内代码

什么是 Markdown

Markdown 是一种方便记忆、书写的纯文本标记语言，用户可以使用这些标记符号以最小的输入代价生成极富表现力的文档：譬如您正在阅读的这份文档。它使用简单的符号标记不同的标题，分割不同的段落，粗体或者斜体某些文字，更棒的是，它还可以

1. 制作一份待办事宜 Todo 列表

支持以 PDF 格式导出文稿
改进 Cmd 渲染算法，使用局部渲染技术提高渲染效率
新增 Todo 列表功能
修复 LaTex 公式渲染问题
新增 LaTex 公式编号功能

2. 书写一个质能守恒公式[^LaTeX]

\[E=mc^2 \]

3. 高亮一段代码[^code]

#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
namespace wing_heart {
    void main() {
        
        }
}
int main() {
    #ifdef LOCAL
    freopen("in.txt","r",stdin);
    freopen("my.out","w",stdout);
    #endif
    wing_heart :: main();
}

Cmd Markdown 支持的全部十九种图表参考

8. 绘制表格

项目	价格	数量
计算机	$1600	5
手机	$12	12
管线	$1	234

答案

根据二项式定理：$(x+y)^n = \sum_{i=0}^n \binom{n}{i} x^i y^{n-i}$

注意到当 $i>m$ 的时候 $\binom{m}{i}=0$，

所以 $F(x) = (1+x)^m$。

再见！

为什么这样证明出来吉司机线段树区间取 min，区间加，区间求和的复杂度是单 log，求找漏洞？（大雾）

省流版：

只讨论进行过取 $\min$ 操作的数。

观察一个区间长度为 $len$ 的线段树节点。我们把极长的值相同的数字成为一个平台。平台个数不小于数字颜色数。势能定义为平台个数。

区间取 $\min$ 会使平台增加 $O(1)$ 个。

单点修改会使平台增加 $O(1)$ 个。

区间加会使边界的平台分裂，多出 $O(1)$ 个，而可能处于操作边界的线段树节点只有 $O(\log n)$ 个。

在没有区间加操作的时候，我们定义一个线段树区间的势能是数字的颜色个数（值相同的数字为同一颜色）。因为每次取 min 递归一次就会把一个区间的最大值和严格次大值合并，势能减 $1$。因此时间复杂度等于总势能。

对于初始的线段树，一个区间长度为 $len$ 的节点势能是 $O(len)$。总势能等于所有节点的区间长度之和，即 $O(n \log n)$。

我们把目光放到一个长度为 $len$ 的区间。

我们建立横轴是下标，数轴是值的坐标系，有 $len$ 个初始点，不妨认为初始点的个数就是势能，即 $len$。这里初始点的个数不小于点的颜色数。

对 $[l,r]$ 的初始点进行取 $\min$ 操作，高处的初始点会“坍塌”到同一高度，形成一个“平台”。我们认为坍塌的点被开除了初始点的名单，成为了一个新的平台。后文平台的定义都是指极大的值相同连续段（不考虑仍然属于初始点的点）。

对于初始点，进行单点和区间加操作不改变势能，因此我们只需要考虑平台的势能。

定义一个区间所有平台的势能等于平台的个数。平台个数不小于属于平台的数的颜色数，所以这么定义是可以的。

一次取 $\min$ 操作会形成或者裂开 $O(1)$ 个平台。容易发现只做取 $\min$ 操作，平台间只存在相邻关系和包含关系（包含就是在一个平台中间再坍塌下去一个小平台）。我们不妨把一个平台包含另一个平台拆开成三个相邻的平台，这不影响平台个数的数量级。因此平台不相交。

对原有平台进行一次单点加操作会生成 $O(1)$ 个新平台。有 $\log n$ 个线段树节点会受此影响。

对原有平台进行一次区间加操作，因为平台不相交，被操作完全覆盖的平台只会整体上下平移，只有边界的 $2$ 个平台会被分裂，因此平台个数增加 $O(1)$ 个。有 $2 \log n$ 个线段树节点可能出现被割开的平台。

因此总复杂度是 $O((n+m) \log n)$ 的。

posted @ 2025-02-09 16:28 wing_heart 阅读(142) 评论(0) 收藏举报

刷新页面返回顶部

wing_heart(:

不开 long long 见祖宗！勤能补拙，菜就多练。

云剪贴板

云剪贴板

做法

代码

第一个出错的数据（模拟赛题数据）

提供对拍代码

题目菱形一种情况证明

欢迎使用 Cmd Markdown 编辑阅读器

二级标题

三级标题

四级标题

五级标题

六级标题

Windows/Mac/Linux 全平台客户端

什么是 Markdown

1. 制作一份待办事宜 Todo 列表

2. 书写一个质能守恒公式[^LaTeX]

3. 高亮一段代码[^code]

Cmd Markdown 支持的全部十九种图表参考

8. 绘制表格

公告

wing_heart(:

不开 long long 见祖宗！ 勤能补拙，菜就多练。

云剪贴板

云剪贴板

做法

代码

第一个出错的数据（模拟赛题数据）

提供对拍代码

题目菱形 一种情况证明

欢迎使用 Cmd Markdown 编辑阅读器

二级标题

三级标题

四级标题

五级标题

六级标题

Windows/Mac/Linux 全平台客户端

什么是 Markdown

1. 制作一份待办事宜 Todo 列表

2. 书写一个质能守恒公式[^LaTeX]

3. 高亮一段代码[^code]

Cmd Markdown 支持的全部十九种图表参考

8. 绘制表格

公告

不开 long long 见祖宗！勤能补拙，菜就多练。

题目菱形一种情况证明