树链剖分

树链剖分

前言

重剖：从去年省选鸽到现在，其实更准确的是从初二下学期第一次学，一直鸽到现在。

笑点解析：重剖：我叫 tree_pou_heavy（重的树剖）

简介

树链剖分就是把树按照某种规定剖成若干条链，便于维护修改和查询。目前我知道的有重链剖分、长链剖分、实链剖分（又称 LCT）。

重链剖分

重链剖分可以维护树上链加、链查、子树加、子树查。基本上有链操作的都可以考虑下重剖（和长剖？）。

每个节点，子树大小（指节点个数）最大的儿子，称为重儿子，其他儿子叫做轻儿子。每个节点和其重儿子连边叫做重边，和其轻儿子连边叫做轻边。把轻边断开，树就被分成了若干条（最多 \(O(n)\) 条）链（一个节点也算一条链）。

我们按照先遍历重儿子，再遍历轻儿子的访问顺序钦定 dfs 序，这样可以保证一条链的 dfs 序是连续的。

我们使用数据结构维护每条链的信息，常见的有线段树维护。

点 \(u,v\) 之间的链，可以划分成若干条树链，我们对每条树链分别进行区间加、区间查询操作即可。对每个节点记录一个 \(top_u\) 表示点 \(u\) 所在的链，深度最小的点是什么。方便跳链。

如果对每条链单独开一棵线段树维护，常数应该会较小，但是如果题目还有子树操作，就必须维护全局的线段树了。

证明点 \(u,v\) 之间有 \(O(\log n)\) 条树链：我们考虑 \(u,lca\) 之间有多少树链。也就是数 \(u,lca\) 之间有多少条轻边。每经过一条轻边从 \(x\) 到达 \(fa_x\)，说明 \(fa_x\) 一定有一个重儿子 \(y\) 满足 \(siz_y \ge sizx\)，因此 \(siz_{fa_x} \ge 2siz_x\)，子树大小会翻倍，而最多翻 \(\log n\) 倍。因此这样的轻边只有 \(O(\log n)\) 条。证毕。

加上线段树复杂度，时间复杂度是 \(O(n \log^2 n)\)。重剖常数是较小的，因为你一般跳不完 \(\log n\) 条链。只是线段树常数较大。但是我们有可爱的 zkw 小常数线段树。

综上，重剖预处理 \(O(n)\)，单次操作 \(O(\log)\) 乘上每条链操作时间复杂度。优点是比较板，需要上树剖的题目一般维护的操作比较雷同（当然你需要先推出操作）。缺点是码量较大。

#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
namespace tree_pou_heavy {
	constexpr int N=1e5+7;
	int n,m,rt,mod;
	int add(int a,int b) { return a+b>=mod ? a+b-mod : a+b; }
	void _add(int &a,int b) { a=add(a,b); }
	void _max(int &a,int b) { a=max(a,b); }
	int a[N];
	int u,v;
	struct edge {
		int to,ne;
	}e[N<<1];
	int head[N],e_cnt;
	void addedge(int u,int v) { e[++e_cnt] = {v, head[u]}; head[u]=e_cnt; }
	struct tree {
		int fa[N],siz[N],gson[N],dep[N];
		int dfn[N],eddfn[N],cnt,idfn[N];
		int top[N];
		void dfs(int u,int f) {
			fa[u]=f;
			dep[u]=dep[f]+1;
			siz[u]=1;
			for(int i=head[u]; i; i=e[i].ne) {
				int v=e[i].to;
				if(v==f) continue;
				dfs(v,u);
				siz[u]+=siz[v];
				if(siz[v]>siz[gson[u]]) gson[u]=v;
			}
		}
		void dfs(int u) {
			dfn[u]=eddfn[u]=++cnt;
			idfn[cnt]=u;
			if(gson[u]) top[gson[u]]=top[u], dfs(gson[u]);
			for(int i=head[u]; i; i=e[i].ne) {
				int v=e[i].to;
				if(v==fa[u] || v==gson[u]) continue;
				top[v]=v, dfs(v);
			}
			eddfn[u]=cnt;
		}
		int tr[N<<2],tag[N<<2];
		int p;
		void build() {
			p=1;
			while(p-2<n) p<<=1;
			rep(i,1,n) tr[p+i]=a[idfn[i]];
			per(i,p-1,1) tr[i]=add(tr[i<<1],tr[i<<1|1]);
		}
		void init() {
			dfs(rt,0);
			top[rt]=rt;
			dfs(rt);
			build();
		}
		void maketag(int u,int x,int siz) { _add(tr[u],1ll*x*siz%mod), _add(tag[u],x); }
		void pushup(int u,int siz) { tr[u]=add(add(tr[u<<1],tr[u<<1|1]),1ll*siz*tag[u]%mod); }
		void _update(int l,int r,int x) {
			l=p+l-1, r=p+r+1;
			int siz=1;
			while(l^r^1) {
				if((l&1)^1) maketag(l^1,x,siz);
				if(r&1) maketag(r^1,x,siz);
				l>>=1, r>>=1, siz<<=1;
				pushup(l,siz), pushup(r,siz);
			} 
			for(l>>=1, siz<<=1; l; l>>=1, siz<<=1) pushup(l,siz);
		}
		int _query(int l,int r) {
			l=p+l-1, r=p+r+1;
			int sizl=0,sizr=0,siz=1;
			int s=0;
			while(l^r^1) {
				if((l&1)^1) _add(s,tr[l^1]), sizl+=siz;
				if(r&1) _add(s,tr[r^1]), sizr+=siz;
				l>>=1, r>>=1, siz<<=1;
				_add(s,1ll*tag[l]*sizl%mod), _add(s,1ll*tag[r]*sizr%mod);
			}
			for(l>>=1, sizl+=sizr; l; l>>=1) _add(s,1ll*tag[l]*sizl%mod);
			return s;
		}
		void update(int u,int v,int x) {
			while(top[u]^top[v]) {
				if(dep[top[u]]<dep[top[v]]) swap(u,v);
				_update(dfn[top[u]],dfn[u],x), u=fa[top[u]];
			}
			if(dfn[u]>dfn[v]) swap(u,v);
			_update(dfn[u],dfn[v],x);
		}
		void update(int u,int x) {
			_update(dfn[u],eddfn[u],x);
		}
		int query(int u,int v) {
			int s=0;
			while(top[u]^top[v]) {
				if(dep[top[u]]<dep[top[v]]) swap(u,v);
				_add(s,_query(dfn[top[u]],dfn[u])), u=fa[top[u]];
			}
			if(dfn[u]>dfn[v]) swap(u,v);
			_add(s,_query(dfn[u],dfn[v]));
			return s;
		}
		int query(int u) {
			return _query(dfn[u],eddfn[u]);
		}
	}T;
	int op,x;
	void main() {
		sf("%d%d%d%d",&n,&m,&rt,&mod);
		rep(i,1,n) sf("%d",&a[i]), a[i]%=mod;
		rep(i,1,n-1) sf("%d%d",&u,&v), addedge(u,v), addedge(v,u);
		T.init();
		rep(i,1,m) {
			sf("%d",&op);
			if(op==1) sf("%d%d%d",&u,&v,&x), T.update(u,v,x);
			else if(op==2) sf("%d%d",&u,&v), pf("%d\n",T.query(u,v));
			else if(op==3) sf("%d%d",&u,&x), T.update(u,x);
			else sf("%d",&u), pf("%d\n",T.query(u));
		}
	}
}
int main() {
	#ifdef LOCAL
	freopen("in.txt","r",stdin);
	freopen("my.out","w",stdout);
	#endif
	tree_pou_heavy :: main();
}

全局平衡二叉树

废话

OI Wiki 把全局平衡二叉树和 LCT 都归到数据结构的动态树了，不过我不知道什么是动态树，所以先归到树剖这里吧。

概述

OI Wiki 讲得很好。

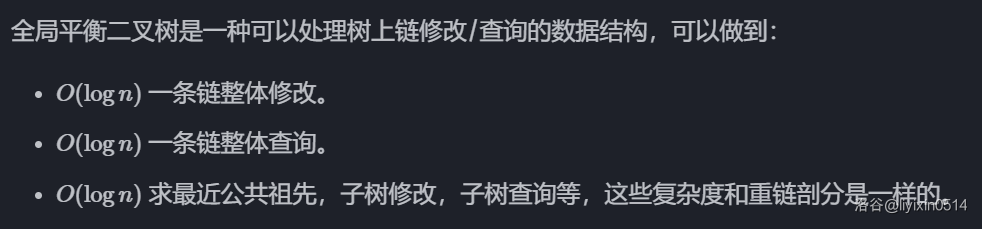
建树 build

  1. 对原树进行重链剖分。
  2. 把每条重链建成一棵二叉树（如何建见下文），然后轻链的两端不变。

这样我们就建好一棵全局平衡二叉树了。最重要的性质是这棵树的树高是 \(O(\log n)\) 的哦！

如何把重链建成二叉树？搬 OI Wiki：

我们先把重链上的点存到数组里，求出每个点轻儿子的子树大小之和加一（即该点本身所贡献的 size）。然后我们按照这个求出这条重链的加权中点，把它作为二叉树的根，两边递归建树，并连上重边。

建出来的二叉树满足中序遍历的顺序符合原重链上深度由浅至深的顺序。

建树的时间复杂度是 \(O(n \log n)\) 的。

证明整棵树高度是 \(O(\log n)\)：

从叶子到根有 \(O(\log n)\) 条轻边。每棵二叉树因为是加权平均，因此左右儿子的大小一定小于该子树大小的一半。所以经过一条重边子树大小会减少至少一半，因此重边至多 \(O(\log n)\) 条。所以总共高度 \(O(\log n)\)。

int gson[N],siz[N];
void dfs(int u) {
	siz[u]=1;
	for(int v : son[u]) {
		dfs(v);
		siz[u]+=siz[v];
		if(siz[v]>siz[gson[u]]) gson[u]=v;
	}
}
int t[N],ts[N],ss[N],ch[N][2],f[N];//装重链的桶、加权前缀和、二叉树子树大小、二叉树两个儿子、全局平衡二叉树父亲
int _build(int l,int r) {//建重链对应二叉树，目前做到区间(l,r]
	int mid=((ts[r]-ts[l])>>1)+ts[l];
	int k=lower_bound(ts+l+1,ts+r+1,mid)-ts;//加权中点
	int u=t[k];
	ss[u]=r-l;
	if(l<k-1) ch[u][0]=_build(l,k-1), f[ch[u][0]]=u;
	if(k<r) ch[u][1]=_build(k,r), f[ch[u][1]]=u;
	return u;
}
int build(int u) {//建树，一条一条重链建
	int x=u;
	do {//先把轻链递归处理，以及连上轻边（仅记录轻边父亲）
		for(int v : son[x]) if(v!=gson[x]) f[build(v)]=x;
	} while(x=gson[x]);
	x=0;
	do {//把重链放进桶，计算加权
		t[++x]=u;
		ts[x]=ts[x-1]+siz[u]-siz[gson[u]];
	} while(u=gson[u]);
	return _build(0,x);
}
void init() {
	dfs(1);//预处理重链
	build(1);//建全局平衡二叉树
}

修改和查询

  • 修改和查询点 \(u\) 到根的链的信息。

就一直跳二叉树即可。注意每个轻边存它的父亲，轻边的父亲（即二叉树的叶子）不需要存轻边，只存二叉树上的儿子。

复杂度 \(O(\log n)\)，轻边 \(O(\log n)\) 条，因为每条重链可以使子树大小减少至少一半，每个二叉树类似于线段树区间操作操作一段深度连续重链区间，其实所有深度比它小的点就是二叉树上在它左边的点。

直接从下往上计算，标记永久化，避免递归，类似 zkw 的优化，可以减少常数。

int tg[N],sum[N];//单个二叉树 子树标记（永久化）、子树和
void add(int u) {
	bool fl=1;
	int x=0;//当前二叉树的当前子树有多少点要加
	while(u) {
		_add(sum[u],x);
		if(fl) {//如果要 u 的左子树（包括 u）
			_add(tg[u],1);//整棵树打标记
			if(ch[u][1]) _add(tg[ch[u][1]],mod-1);//右子树不打标记，容斥掉
			_add(x,ss[ch[u][0]]+1);//更新祖先时用
			_add(sum[u],mod-ss[ch[u][1]]);//因为标记永久化了，容斥掉不要的部分
		}
		fl=u!=ch[f[u]][0];
		if(fl && u!=ch[f[u]][1]) x=0;//跳过轻边
		u=f[u];
	}
}
int query(int u) {
	int ans=0;
	int fl=1;
	int x=0;//当前子树要了多少个点
	while(u) {
		if(fl) {//如果要左子树和 u 自己
			_add(ans,add(sum[u],mod-sum[ch[u][1]]));
			_add(ans,mod-mul(tg[ch[u][1]],ss[ch[u][1]]));
			_add(x,ss[ch[u][0]]+1);
		}
		_add(ans,mul(x,tg[u]));
		fl=u!=ch[f[u]][0];
		if(fl && u!=ch[f[u]][1]) x=0;
		u=f[u];
	}
	return ans;
}

经验

P4211 [LNOI2014] LCA 模板题

把求 LCA 深度转化为到跟链加和查询。然后拍全局平衡二叉树板子，时间复杂度 \(O((n+m)\log n)\)。

code

posted @ 2024-11-26 17:01  wing_heart  阅读(49)  评论(0)    收藏  举报