线段树
线段树
线段树有很强的拓展性,因此这篇 blog 可以写很长,我会边学习边补充。
记得开 4 倍空间!!!
线段树模板 code
#include<bits/stdc++.h>
#define ll long long
#define pf printf
#define sf scanf
using namespace std;
const int N=1e5+7;
int tr[N*4];
int f[N*4];
int a[N];
int n,q;
int l,r,val;
void build(int u,int l,int r){
if(l==r){
tr[u]=a[l];
return;
}
int mid=(l+r)/2;
build(u*2,l,mid);
build(u*2+1,mid+1,r);
tr[u]=tr[u*2]+tr[u*2+1];
}
void pushdown(int u,int l,int r){
if(l==r){
tr[u]+=f[u];
f[u]=0;
return;
}
tr[u]+=f[u]*(r-l+1);
f[u*2]+=f[u];
f[u*2+1]+=f[u];
f[u]=0;
}
void add(int u,int L,int R,int l,int r,int val){
if(l>=L&&r<=R){
f[u]+=val;
return;
}
int mid=(l+r)/2;
pushdown(u,l,r);
if(mid>=L) add(u*2,L,R,l,mid,val);
if(mid+1<=R) add(u*2+1,L,R,mid+1,r,val);
}
int ask(int u,int L,int R,int l,int r){
if(l>=L&&r<=R){
pushdown(u,l,r);
return tr[u];
}
int mid=(l+r)/2;
int sum=0;
pushdown(u,l,r);
if(mid>=L) sum+=ask(u*2,L,R,l,mid);
if(mid+1<=R) sum+=ask(u*2+1,L,R,mid+1,r);
return sum;
}
int main(){
sf("%d",&n);
for(int i=1;i<=n;i++) sf("%d",&a[i]);
build(1,1,n);
sf("%d",&q);
while(q--){
int op;
sf("%d%d%d",&op,&l,&r);
if(op==1){
sf("%d",&val);
add(1,l,r,1,n,val);
}else{
pf("%d\n",ask(1,l,r,1,n));
}
}
//利用线段树进行一些操作
}
经验
法阵(线段树降 \(\log\))
zkw 线段树
简介
zkw 线段树是线段树的一种循环而非递归写法,常数小一半,可以用来卡常。
参考及图片来源:zkw 线段树-原理及其扩展
上面这个链接挂了 www
建树
维护 \(n\) 个位置的信息,需要开至少 \(n+2\) 个叶子结点,其中最左边和最右边的叶子结点是虚点,不维护实际信息。
为了方便找父亲,叶子结点个数是 \(2\) 的幂。
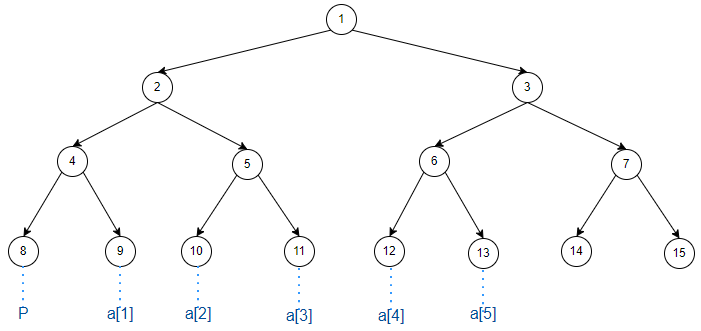
我们先找出 \(P\) 的编号。\(P\) 的编号一定是 \(2\) 的幂次,满足 \(P-1 > n\)。
void build() {
p=1;
while(p-2<n) p<<=1;
rep(i,1,n) sum[p+i]=a[i];
per(i,p-1,1) sum[i]=sum[i<<1]+sum[i<<1|1];
}
上传
由于儿子父亲的倍数关系和普通线段树是一样的,因此上传和普通线段树一样。
这里给出标记永久化的代码。
void pushup(int u,int siz) { sum[u]=sum[u<<1]+sum[u<<1|1]+tag[u]*siz; }
修改
单点修改
直接修改叶子(结点 \(P+x\))然后循环上传。
区间修改
为了进一步减小常数,可以标记永久化,以减少下放标记的常数。
区间左右两边设两个虚点,叫做哨兵结点。
对于左哨兵 \(S\),当它是左儿子时,其兄弟节点是需要用到的;
对于右哨兵 \(T\),当它是右儿子时,其兄弟节点是需要用到的。
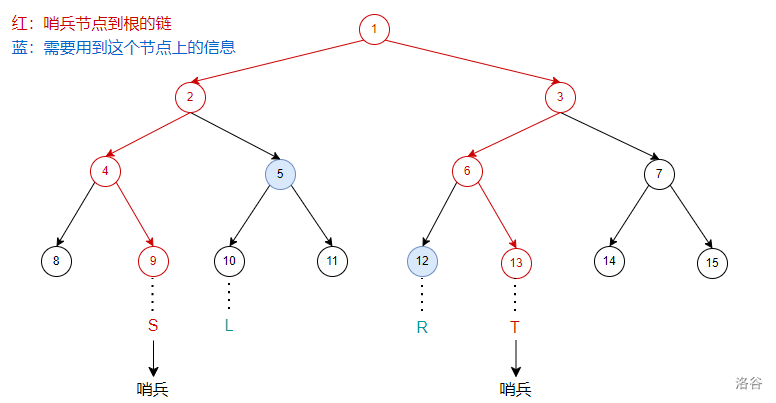
void update(int l,int r,ll x) {
int L=p+l-1,R=p+r+1;
int siz=1;
while(L^R^1) {
if((L&1)^1) sum[L^1]+=x*siz, tag[L^1]+=x;
if(R&1) sum[R^1]+=x*siz, tag[R^1]+=x;
L>>=1, R>>=1, siz<<=1;
pushup(L,siz),pushup(R,siz);
}
for(L>>=1,siz<<=1;L;L>>=1,siz<<=1) pushup(L,siz);
}
区间查询
仍然是钦定哨兵节点,注意标记永久化之后答案的累计。
ll query(int l,int r) {
ll s=0;
int L=p+l-1,R=r+p+1;
int sizl=0,sizr=0,siz=1;
while(L^R^1) {
if((L&1)^1) s+=sum[L^1], sizl+=siz;
if(R&1) s+=sum[R^1], sizr+=siz;
L>>=1, R>>=1, siz<<=1;
s+=tag[L]*sizl+tag[R]*sizr;
}
for(L>>=1,sizl+=sizr;L;L>>=1) s+=tag[L]*sizl;
return s;
}
可持久化线段树(主席树)
详细讲解可以看这篇题解
P3919 【模板】可持久化线段树 1(可持久化数组)(单点修改、单点查询)
code
#include<bits/stdc++.h>
// #define LOCAL
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
#define isdigit(x) (x>='0')
#define gc getchar_unlocked
#define pc(x) putchar_unlocked(x)
template <typename T>
void read(T &x) {
x=0;
T fl=1;
char ch=gc();
for(;!isdigit(ch);ch=gc()) if(ch=='-') fl=-1;
for(;isdigit(ch);ch=gc()) x=(x<<3)+(x<<1)+(ch^48);
x=x*fl;
}
template <typename T>
void write(T x,char ch) {
if(x<0) pc('-'),x=-x;
static int st[20];
int top=0;
do {
st[top++]=x%10;
x/=10;
}while(x);
while(top) pc(st[--top]^48);
pc(ch);
}
typedef long long ll;
const int N=1e6+7;
int n,m,a[N];
int t,op,x,val;
int rt[N];
struct segtree {
struct node {
int val,ls,rs;
}tr[N<<5];
int cnt;
void build(int &u,int l,int r) {
u=++cnt;
if(l==r) { tr[u].val=a[l]; return; }
int mid=(l+r)>>1;
build(tr[u].ls,l,mid), build(tr[u].rs,mid+1,r);
}
void update(int &u,int v,int l,int r,int x,int val) {
u=++cnt;
tr[u]=tr[v];
if(l==r) { tr[u].val=val; return; }
int mid=(l+r)>>1;
if(x<=mid) update(tr[u].ls,tr[v].ls,l,mid,x,val);
else update(tr[u].rs,tr[v].rs,mid+1,r,x,val);
}
int query(int u,int l,int r,int x) {
if(l==r) return tr[u].val;
int mid=(l+r)>>1;
if(x<=mid) return query(tr[u].ls,l,mid,x);
return query(tr[u].rs,mid+1,r,x);
}
}T;
int main() {
#ifdef LOCAL
freopen("in.txt","r",stdin);
freopen("my.out","w",stdout);
#endif
read(n),read(m);
rep(i,1,n) read(a[i]);
T.build(rt[0],1,n);
rep(i,1,m) {
read(t),read(op);
if(op==1) {
read(x),read(val);
T.update(rt[i],rt[t],1,n,x,val);
}else{
read(x);
rt[i]=rt[t];
write(T.query(rt[i],1,n,x),'\n');
}
}
}
P3834 【模板】可持久化线段树 2(静态区间询问第 \(k\) 小)(可以转化成单点插入,询问一段时间的第 \(k\) 大可以线段树二分)
code
#include<bits/stdc++.h>
// #define LOCAL
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
const int N=2e5+7;
int n,m,a[N];
int b[N];
int rt[N];
struct segtree {
struct node {
int cnt,ls,rs;
}tr[N<<5];
int cnt;
void build(int &u,int l,int r) {
u=++cnt;
if(l==r) return;
int mid=(l+r)>>1;
build(tr[u].ls,l,mid), build(tr[u].rs,mid+1,r);
}
void pushup(int u) { tr[u].cnt=tr[tr[u].ls].cnt+tr[tr[u].rs].cnt; }
void insert(int &u,int v,int l,int r,int x) {
u=++cnt;
tr[u]=tr[v];
if(l==r) { tr[u].cnt++; return; }
int mid=(l+r)>>1;
if(x<=mid) insert(tr[u].ls,tr[v].ls,l,mid,x);
else insert(tr[u].rs,tr[v].rs,mid+1,r,x);
pushup(u);
}
int query(int u,int v,int l,int r,int k) {
if(l==r) return l;
int mid=(l+r)>>1;
int tmp=tr[tr[u].ls].cnt-tr[tr[v].ls].cnt;
if(tmp>=k) return query(tr[u].ls,tr[v].ls,l,mid,k);
return query(tr[u].rs,tr[v].rs,mid+1,r,k-tmp);
}
}T;
int l,r,k;
int main() {
#ifdef LOCAL
freopen("in.txt","r",stdin);
freopen("my.out","w",stdout);
#endif
sf("%d%d",&n,&m);
rep(i,1,n) sf("%d",&a[i]), b[i]=a[i];
sort(b+1,b+n+1);
T.build(rt[0],1,n);
rep(i,1,n) a[i]=lower_bound(b+1,b+n+1,a[i])-b,T.insert(rt[i],rt[i-1],1,n,a[i]);
rep(i,1,m) {
sf("%d%d%d",&l,&r,&k);
pf("%d\n",b[T.query(rt[r],rt[l-1],1,n,k)]);
}
}
主席树区间修改,时间复杂度显然不变,空间复杂度每次修改是 \(4 \log n\) 的。
线段树合并
时间复杂度有点玄学,正常是 \(O(n \log n)\),常数有点大。
线段树合并是用于合并若干棵线段树信息的科技,而且不难写。
线段树合并一般用于合并值域线段树。首先需要动态开点线段树。有值的地方才开 \(\log\) 个点。
主要部分是 merge 函数,原理类似平衡树合并。
合并到 \(x,y\),如果 \(x\) 为空,返回 \(y\),如果 \(y\) 为空,返回 \(x\)。如果都不为空,分别合并两个儿子。如果是叶子,直接合并。最后上传更新。
主要代码(指针写法)
struct node{
node (int _l,int _r) :l(_l),r(_r),mx(0),mxid(0),ls(nullptr),rs(nullptr){}
int l,r,mx,mxid;
node *ls,*rs;
inline int getmid() { return (l+r)>>1; }
inline void pushup() {
mx=0,mxid=0;
if(ls!=nullptr) if(ls->mx>mx) mx=ls->mx,mxid=ls->mxid;
if(rs!=nullptr) if(rs->mx>mx) mx=rs->mx,mxid=rs->mxid;
}
};
void insert(node *u,int x,int val) {
if(u->l==u->r) {
u->mx+=val;
if(u->mx<=0) u->mxid=0;
else u->mxid=x;
return ;
}
int mid=u->getmid();
if(x<=mid) insert(u->ls==nullptr?u->ls=new node (u->l,mid):u->ls,x,val);
else insert(u->rs==nullptr?u->rs=new node(mid+1,u->r):u->rs,x,val);
u->pushup();
}
node * merge(node *x,node *y) {
if(x==nullptr) return y;
if(y==nullptr) return x;
if(x->l==x->r) {
/*
把 y 合并到 x
*/
return x;
}
x->ls=merge(x->ls,y->ls),x->rs=merge(x->rs,y->rs);
x->pushup();
return x;
}
node * solve(int u) {
node *rt=new node(1,V);
/*
向结点 u 的 rt insert 一些东西
*/
for(int i=head[u];i;i=e[i].ne) {
int v=e[i].to;
if(v==fa[u]) continue;
node * rtv=solve(v);
rt=merge(rt,rtv) ;
}
/*
处理答案
*/
return rt;
}
经验
P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并 板子题为什么不是一眼 dsu 做
吉司机线段树(势能线段树)
适用于需要区间取 \(\min or \max\) 操作的情况。
下面介绍取 \(\min\) 的做法,取 \(\max\) 同理。
在维护朴素的线段树的数据下,再维护区间最大值 \(fi\)、次大值 \(se\)、最大值个数 \(len_0\)、最大值懒标记 \(tag_0\)。这些数据的上传和下放没什么特别难的,不细讲。
加法修改和询问同朴素线段树。
对于区间对 \(x\) 取 \(\min\) 操作,分以下情况:
- \(x\ge fi\),不需要进行修改;
- \(fi> x \ge se\),只需要修改最大值;
- \(se > x\),递归左右儿子修改。
势能线段树的时间复杂度采用势能分析法。设总势能是线段树每个区间的颜色数之和。显然初始势能是 \(O(n \log n)\),每次区间最值操作时如果递归下去,势能至少减 \(1\),因此总时间复杂度等于总势能(初始势能加上操作带来的势能增量)。
带单点加操作,时间复杂度不变。可以证明单点操作不影响势能增量的数量级。
带区间加操作,由于势能的增量,总时间复杂度是 \(O(n \log^2 n)\) 的,势能的分析与单点操作的不同。但是据原论文,实际实现接近单 \(\log\)。无所谓,反正本来常数就大。
同时存在取 \(\min\) 和取 \(\max\) 操作一般不影响时间复杂度。
错误的时间复杂度证明
可以发现,单次修改操作有可能是 \(O(n\log n)\) 的。下面我们用势能分析法证明它的总时间复杂度不超过 \(O(n\log n)\)。
设线段树每个节点对应的区间包含的本质不同的数字的总数是 \(k\),显然 \(k\le n\log n\)。我们把 \(k\) 称为势能(有一个专门的符号表示势能的,显然我忘记了)。
每次取 \(\min\) 操作往下递归一次,说明至少 \(fi\) 和 \(se\) 会被修改成 \(x\),则势能 \(k\) 至少减 \(1\)。因为 \(k>0\),因此这个取 \(min\) 操作的总时间复杂度不超过 \(k\)。
但是单点修改和区间加有可能增加势能。
\(k\) 被增加当且仅当本质相同的数变得不同。
一次单点修改操作会影响 \(\log\) 个节点的势能,总共最多使 \(k\) 增加 \(n\log n\),不影响时间复杂度。
对于一次区间加操作,可能影响 \(n\log n\) 个节点。
对于一个区间,我们把相等的数组成的集合,且数量至少为 \(2\) 的集合叫做一个[平台](数字不一定是连续区间),原始区间可能就会有几个[原始平台],而取 \(\min\) 操作造成的平台称为 [人造平台]。
对于一个区间,区间加操作能增加的势能上界等于平台个数,而一个平台的最大贡献次数不超过平台长度,这是显然的,因为每次贡献都会把这个平台拆成两个人造平台。
对于所有原始平台,他们的总贡献不超过 \(O(n\log n)\),不影响时间复杂度。所以我们讨论人造平台。
对于一个线段树节点,进行一次区间取 \(\min\) 操作,至多增加一个人造平台。在一个人造平台的范围内,不会存在比这个平台高的数字。如果我们把一个人造平台包含另一个人造平台的情况看做三个相邻的人造平台,就会发现人造平台的范围不会相交。那么每次区间加操作,如果覆盖了整个人造平台的范围,则这个人造平台不会分裂,没有贡献。因此每次区间加操作对于一层的线段树节点,只会使两端的节点增加 \(O(1)\) 的势能。一共 \(\log\) 层。也就是说每次区间加操作最多增加 \(\log\) 的势能,总势能增加量 \(n\log n\),不影响时间复杂度。
综上所述,吉司机线段树的时间复杂度是 \(O(n\log n)\) 的。
模板题目
(同一道题)
关键代码
struct tree{
int sum,ch[2]/*最大/次大值*/,len[2]/*最大值个数/其余个数*/,tag[2]/*最大值懒标记/其余懒标记*/;
};
struct jsj{
tree tr[N<<2];
void pushup(int u){
int ls=u<<1,rs=u<<1|1;
tr[u].sum=tr[ls].sum+tr[rs].sum;
if(tr[ls].ch[0]==tr[rs].ch[0]) {
tr[u].ch[0]=tr[ls].ch[0];
tr[u].ch[1]=max(tr[ls].ch[1],tr[rs].ch[1]);
tr[u].len[0]=tr[ls].len[0]+tr[rs].len[0];
tr[u].len[1]=tr[ls].len[1]+tr[rs].len[1];
}else {
if(tr[ls].ch[0]<tr[rs].ch[0]) swap(ls,rs);
tr[u].ch[0]=tr[ls].ch[0];
tr[u].ch[1]=max(tr[ls].ch[1],tr[rs].ch[0]);
tr[u].len[0]=tr[ls].len[0];
tr[u].len[1]=tr[ls].len[1]+tr[rs].len[0]+tr[rs].len[1];
}
}
void pushdown(int u){
int ls=u<<1,rs=u<<1|1;
if(tr[ls].ch[0]==tr[rs].ch[0]) {
rep(0,1,i) tr[ls].ch[i]+=tr[u].tag[i],tr[rs].ch[i]+=tr[u].tag[i],
tr[ls].sum+=tr[u].tag[i]*tr[ls].len[i],tr[rs].sum+=tr[u].tag[i]*tr[rs].len[i],
tr[ls].tag[i]+=tr[u].tag[i],tr[rs].tag[i]+=tr[u].tag[i];
}else{
if(tr[ls].ch[0]<tr[rs].ch[0]) swap(ls,rs);
tr[ls].ch[0]+=tr[u].tag[0],tr[rs].ch[0]+=tr[u].tag[1];
tr[ls].ch[1]+=tr[u].tag[1],tr[rs].ch[1]+=tr[u].tag[1];
tr[ls].sum+=tr[u].tag[0]*tr[ls].len[0],tr[ls].sum+=tr[u].tag[1]*tr[ls].len[1];
tr[rs].sum+=tr[u].tag[1]*(tr[rs].len[0]+tr[rs].len[1]);
tr[ls].tag[0]+=tr[u].tag[0];tr[rs].tag[0]+=tr[u].tag[1];
tr[ls].tag[1]+=tr[u].tag[1];tr[rs].tag[1]+=tr[u].tag[1];
}
tr[u].tag[0]=tr[u].tag[1]=0;
}
void change(int u,int l,int r,int x,int val){//单点修改
if(l==r){
tr[u].ch[0]=val;
tr[u].len[0]=1;
tr[u].ch[1]=tr[u].len[1]=tr[u].tag[0]=tr[u].tag[1]=0;
tr[u].sum=val;
return;
}
int mid=(l+r)>>1;
pushdown(u);
if(x<=mid) change(u<<1,l,mid,x,val);
else change(u<<1|1,mid+1,r,x,val);
pushup(u);
}
void add(int u,int l,int r,int L,int R){//区间加1(可以改成加 x )
if(l>=L&&r<=R){
tr[u].sum+=tr[u].len[0]+tr[u].len[1];
tr[u].ch[0]++;
tr[u].ch[1]++;
tr[u].tag[0]++,tr[u].tag[1]++;
return;
}
int mid=(l+r)>>1;
pushdown(u);
if(mid>=L) add(u<<1,l,mid,L,R);
if(mid+1<=R) add(u<<1|1,mid+1,r,L,R);
pushup(u);
}
void qmin(int u,int l,int r,int L,int R,int x){//区间对 x 取 min
if(l>=L&&r<=R){
if(x>=tr[u].ch[0]) return;
if(x<=tr[u].ch[1]) {
int mid=(l+r)>>1;
pushdown(u);
qmin(u<<1,l,mid,L,R,x);
qmin(u<<1|1,mid+1,r,L,R,x);
pushup(u);
return;
}
tr[u].tag[0]-=tr[u].ch[0]-x;
tr[u].sum-=(tr[u].ch[0]-x)*tr[u].len[0];
tr[u].ch[0]=x;
return;
}
int mid=(l+r)>>1;
pushdown(u);
if(mid>=L) qmin(u<<1,l,mid,L,R,x);
if(mid+1<=R) qmin(u<<1|1,mid+1,r,L,R,x);
pushup(u);
}
};
本文来自博客园,作者:wing_heart,转载请注明原文链接:https://www.cnblogs.com/wingheart/p/18357759


 浙公网安备 33010602011771号
浙公网安备 33010602011771号