计算几何基础

计算几何基础

点积和差积

点积

两个二维向量点积的结果是一个数量。

点积又叫做向量积、内积，向量 \(a,b\) 的点积 \(a \cdot b\) 是：

\[x_ax_b + y_ay_b \]

几何意义下的式子是：\(\| a \| \| b \| \cos \theta\)。

几何意义是 \(b\) 的模长乘向量 \(a\) 投影到 \(b\) 的模长。

证明几何式子和坐标式子相同：将 \(a,b\) 正交分解。

不难发现点积满足交换律。事实上点积满足乘法的所有运算法则。

在计算几何里，可以使用点积判断两个向量的左右关系（其实就是 \(\cos \theta\) 的正负）。

叉积

也叫外积。

二维向量的叉积是一个数量。

二维向量 \(a,b\) 的叉积 \(a \times b\) 定义为：

\[x_ay_b - x_by_a \]

几何式子是：\(\| a \| \| b \| \sin \theta\)。

其几何含义为以 \(a,b\) 为邻边的平行四边形的面积（注意当 \(b\) 在 \(a\) 下方时差积为负数）

容易发现叉积满足 \(a \cdot b = - b \cdot a\)（反交换律）。叉积也满足结合律和分配率。

在计算几何中，二维叉积可以用来判断两个向量的上下关系，即 \(\sin \theta\) 的正负。

基本的叉积是指三维差积，三维向量 \(a,b\) 的差积 \(s \times b\) 是：

\[(y_a z_b - z_a y_b, z_a x_b - x_a z_b, x_a y_b - y_a x_b) \]

这是一个三维向量，其方向垂直于 \(a,b\) 形成的平面。

其方向可以通过右手螺旋定则判断，具体地，右手四指自然地从 \(a\) 的方向弯曲指向 \(b\) 的方向，大拇指弹出来的方向就是叉乘结构的方向。

三维叉乘同样满足反交换律（方向也是反的哦）。

判定点和多边形的关系

简介

射线法。时间复杂度 \(O(n)\)。

参考【计算几何】判断一个点是否在多边形内部。

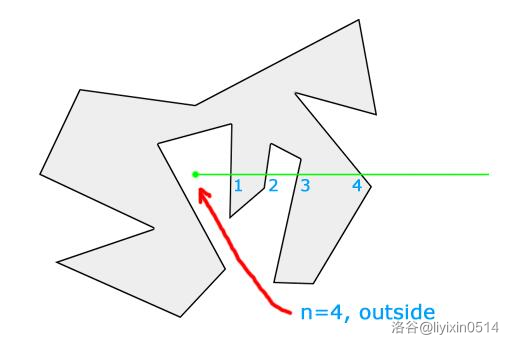
如图，对要判定的点向某个方向（以正右方为例）引一条射线，数射线与多边形交点个数 \(n\)，若 \(n\) 是奇数，则点在多边形内，否则点在多边形外。

枚举多边形的每一条边，判定是否存在交点。

正确性证明略。

特殊情况

1. 点在多边形上

这种情况就在枚举每一条边的时候判定点是否在边上（包括两端）就可以了。

2. 射线经过多边形顶点

这种情况应该算几个交点呢？

参考博客里讲得很清楚。

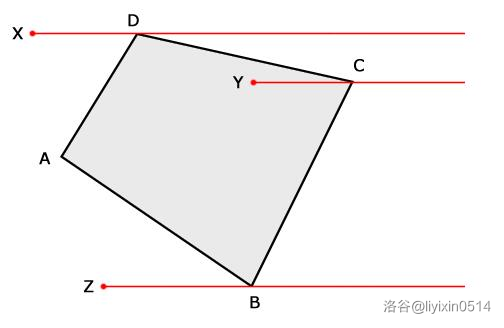
我们把多边形的 \(y\) 左边变成上开下闭的形式。即每个点 \((x,y)\) 变成点 \((x,y-eps)\)。酱紫就不会有射线交到多边形节点上面的情况了，而且可以发现是正确的。

判定点与凸多边形的关系

极点法。

可以 \(O(\log n)\) 求解，\(n\) 为凸包点数。

参考 UVA - 13024 Saint John Festival 凸包+二分

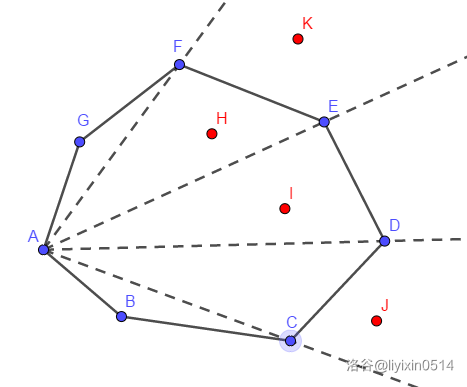
对凸包上的点按照其斜率排序，然后二分找出需要判定的点在哪两个向量之间，然后使用差积判定点是否在三角形内部。

如图，点 \(H,K\) 均在向量 \(AF,AE\) 之间，于是我们计算 \(FH,HE\) 的差积，得到负数，说明 \(H\) 在三角形内部，计算 \(FK,KE\) 的差积，得到正数，说明 \(K\) 在三角形外部。如果点在三角形边 \(FE\) 上，差积将会是 \(0\)。

code

注意凸包的极点（\(s_1\)）必须平移至 \((0,0)\)。

bool query(point *s,point x) {//若 x 在凸包 s 内，返回 1，否则返回 0
	if(x*s[2]>0 || c[cnt]*x>0 || (x*c[2]==0 && calc(x,{0,0})>calc(c[2],{0,0})) || (c[cnt]*x==0 && calc(x,{0,0})>calc(c[cnt],{0,0}))) return 0;//x 不在任何一个三角形范围内
	int k=lower_bound(c+2,c+cnt+1,x,cmp2)-c-1;//找出逆时针方向 x 的前一个向量。
	return (x-c[k])*(c[k+1]-x)<=0;//根据差积判定
}

凸包

在一个平面直角坐标系中，有 \(n\) 个点，以其中一些点为顶点覆盖了所有点且所有内角都小于 \(180^{\circ}\) 的多边形即为这 \(n\) 个点的凸包。

形象点说，就像在平面上的 \(n\) 根柱子外围套一根皮筋，皮筋就是凸包。

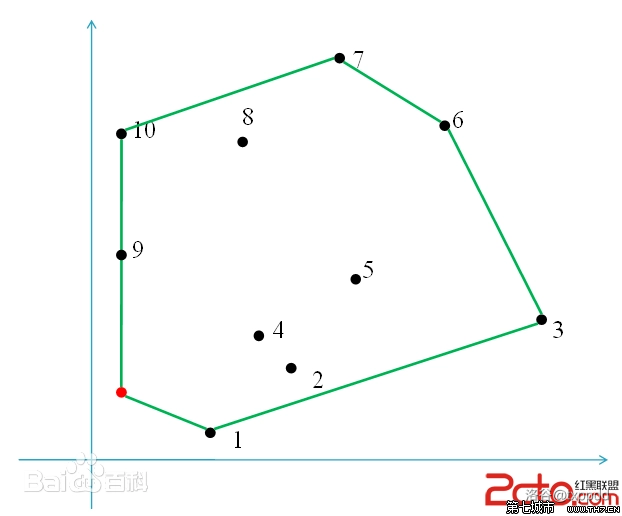
求凸包

Graham扫描法

给定 \(n\) 个点，\(O(n)\) 求凸包。

参考：知乎——算法学习笔记(65): 凸包

知乎专栏写得很好，这里简单概述。

容易发现，平面上最左、最上的点一定是在凸包上的，我们把这个点称为极点。我们进行极角排序，即以极点为原点，所有点按照其斜率从小到大排序，将排序后的点依次相连就可以得到一个包含所有点的多边形，但是不一定是凸多边形。

然后我们按照排序的顺序遍历所有点，构成凸包的边是逆时针方向旋转的，可以使用叉乘判断，如果不符合逆时针，就把上一个点 pop 出。

这样就可以求出凸包了。

code

struct point {
	int x,y;
	point operator - () const { return {-x,-y}; }
	point operator + (const point b) const { return {x+b.x, y+b.y}; }
	point operator - (const point b) const { return *this + (-b); }
	ll operator * (const point b) const { return 1ll*x*b.y - 1ll*y*b.x; }
};
ll chengfang(ll x) { return x*x; }
ll calc(point a,point b) { return chengfang(a.x-b.x)+chengfang(a.y-b.y); }
bool cmp (point a,point b) {
	ll x=(a-tmp)*(b-tmp);//差积
	if(x==0) return calc(a,tmp) < calc(b,tmp);
	return x>0;
}
int st[N<<1];
void get_tubao(point *p, int &n) {
	int rt=1;
	rep(i,2,n) if(p[i].y<p[rt].y || (p[i].y==p[rt].y&&p[i].x<p[rt].x)) rt=i;//找极点
	swap(p[1],p[rt]); tmp=p[1];
	sort(p+2,p+n+1,cmp);//极点排序
	int top=0;
	st[++top]=1, st[++top]=2;
	rep(i,3,n) {//使用栈求凸包
		while(top>1 && (p[i]-p[st[top]])*(p[st[top]]-p[st[top-1]])>=0) --top;
		st[++top]=i;
	}
	n=top;
	rep(i,1,n) p[i]=p[st[i]];
}

凸壳

不封闭的凸包。

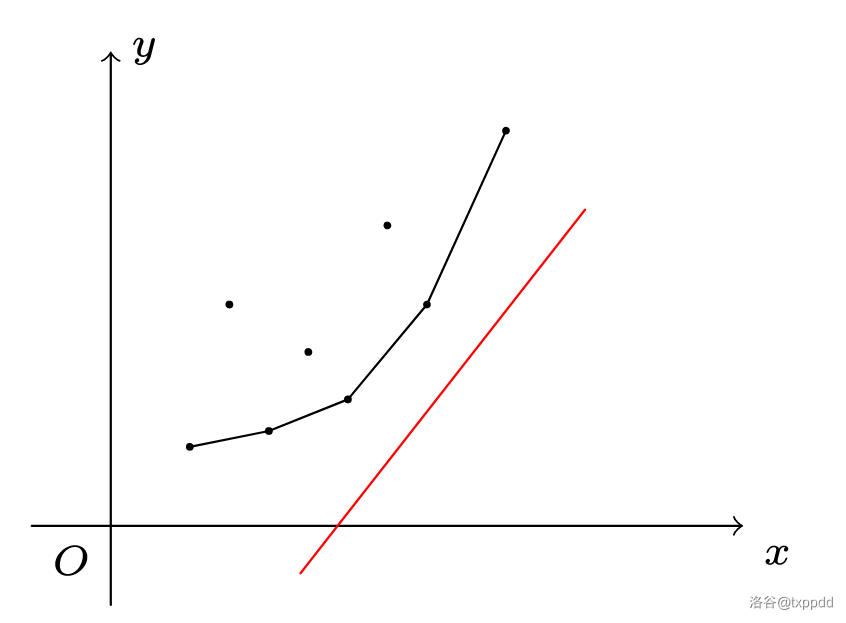
性质

以上图的下凸壳为例：

1. 所有点都在凸壳里面（毕竟凸壳是凸包的一部分）；
2. 凸壳上相邻两点连成的直线斜率随 \(x\) （或 \(y\)）的增大单调递增或递减（上图为单调递增）。

维护凸壳

单调队列维护（继续以下凸壳为例）

要求：

新加入的点必须 \(x\) 单调递增。

步骤：

设 \(K(a,b)\) 表示经过点 \(a,b\) 的直线的斜率，即 \(|y_a-y_b|\div |x_a-x_b|\)。设 \(q_j\) 表示凸壳中第 \(j\) 个点的编号。

需要加入点 \((x_i,y_i)\)，当前凸壳共有 \(k\) 个点；

若 \(K(q_{k-1},q_k)>=K(q_k,i)\),把 \(q_k\) 从凸壳中踢出；

重复直到 \(K(q_{k-1},q_k)<K(q_k,i)\)，将点 \(i\) 加入凸壳；

Code

#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define il inline
using namespace std;
typedef long long ll;
const int N=1e5+7;
int n;
int x[N],y[N];
int q[N],k;
long double K(int a,int b) { return 1.0*abs(y[a]-y[b])/abs(x[a]-x[b]); }
int main(){
	sf("%d",&n);
	for(int i=1;i<=n;i++){
		sf("%d%d",&x[i],&y[i]);
		if(k>1)
		while(K(q[k-1],q[k])>=K(q[k],i)&&k>1) k--;
		q[++k]=i;
	}
}