Image Based Lighting: Diffuse irradiance

在之前的文章里，我们介绍了直接光照的PBR的实现。今天，我们将介绍基于Image Based Lighting（IBL）技术的PBR间接光照的实现方法。
IBL技术是是一类光照技术的集合，它认为可以将周围的环境贴图看成是构成物体间接光照的来源。它环境贴图的每个像素视为光源，在渲染方程中直接使用它。这种方式可以有效地捕捉环境的全局光照和氛围，使物体更好地融入其环境。

Envrionment Map

环境贴图一般分为CubeMap、EquirectangularMap等等，具体的实现大同小异。我们使用EquirectangularMap来构建环境贴图，下图就是一张基于EquirectangularMap的环境贴图：

sIBL Archive网站中有很多这种类似的环境贴图。

这类贴图一般来说都是基于HDR的图片，我们可以借助stb_image.h这个库来实现对hdr文件的读取，具体函数如下：

int nrComponents;
data = stbi_loadf(path.c_str(), &width, &height, &nrComponents, 0);

然后我们创建相应的ShaderResourceView:

D3D11_TEXTURE2D_DESC texDesc;
texDesc.Width = width;
texDesc.Height = height;
texDesc.MipLevels = 1;
texDesc.ArraySize = 1;
texDesc.Format = DXGI_FORMAT_R32G32B32_FLOAT;
texDesc.SampleDesc.Count = 1;
texDesc.SampleDesc.Quality = 0;
texDesc.Usage = D3D11_USAGE_DEFAULT;
texDesc.BindFlags = D3D11_BIND_SHADER_RESOURCE;
texDesc.CPUAccessFlags = 0;
texDesc.MiscFlags = 0;

D3D11_SUBRESOURCE_DATA initData = { 0 };
initData.SysMemPitch = width * sizeof(XMFLOAT3);

initData.pSysMem = data;

ID3D11Texture2D* tex = 0;
device->CreateTexture2D(&texDesc, &initData, &tex);

HRESULT hr = device->CreateShaderResourceView(tex, 0, &environmentSRV);
ReleaseCOM(tex);

initData.SysMemPitch = width * sizeof(XMFLOAT3);
initData.pSysMem = data;

这样就构成了获得了这张环境贴图的SRV。
接下来我们介绍一下如何将这张贴图渲染出来，在场景中表现为一个环绕着场景的背景图。
我们可以创建一个非常非常大的圆球，然后将这张贴图映射到这个圆球里，并渲染出来就可以了。那么圆球的顶点和贴图像素之间的映射关系是如何的呢？
对于EquirectangularMap（也就是我们上面展示的图），它的每一个像素实际上是可以映射到球坐标系的 \(\theta\) 和 \(\phi\)，\(\phi\)的范围是[-\(\pi\)，\(\pi\)]，\(\theta\)的范围是[\(-\frac{\pi}{2}\)，\(\frac{\pi}{2}\)]。
那么对于EquirectangularMap的纹理坐标系，其x轴的范围[0,1]就线性对应[-\(\pi\)，\(\pi\)]，y轴[0,1]线性对应[\(-\frac{\pi}{2}\)，\(\frac{\pi}{2}\)]。那么已知圆球的顶点到中心的方向v，该顶点所对应的纹理坐标就呼之欲出了。下面展示渲染环境贴图的PixelShader：

float2 getSphericalMapTexCoord(float phi, float theta)
{
      //将phi、theta映射到纹理坐标
      return float2((theta + PI) / (2.0 * PI), (phi + PI * 0.5) / PI);
}

float4 PS(VertexOut pin) : SV_Target
{
      //圆球的中心是原点，因此可以根据某个顶点直接获取该顶点到圆心的方向
      //然后分解出该方向在球坐标中的phi和theta
      float3 vec = normalize(pin.PosW.xyz);
      float theta = atan2(vec.z, vec.x);
      float phi = asin(vec.y);

      float2 tex_coord = getSphericalMapTexCoord(phi, theta);
      float3 color = gEnvironmentMap.Sample(samLinear, tex_coord, 0.0f).rgb;

      //因为是HDR图像，所以还要进行Gamma矫正
      color = color / (color + 1.0);
      color = pow(color, 1.0 / 2.2);

      return float4(color, 1.0);
}

具体算法可以参考一下这个网站所介绍的算法。
经过以上步骤，我们就可以将环境贴图在场景中渲染出来了：

当然，用CubeMap等贴图也是可以做出差不多的效果的，在这里我们就不赘述了。

Diffuse Irradiance

得到了EnvrionmentMap后，我们就可以利用它来计算基于PBR的间接光照。我们再来看一下反射方程：

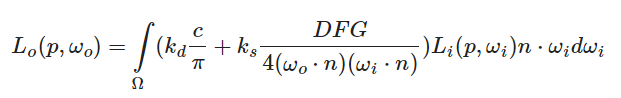
在Shader中计算这个积分需要将场景的辐照度累加起来，如果实时来做会大大降低帧率。因此我们预先将积分存储在一个贴图中，在实际渲染时，使用一个方向向量\(\omega_i\)对此贴图进行采样，我们就可以获取该方向上的场景辐照度，如以下伪代码所示：

float3 irradiance = gIrradianceMap.Sample(samLinear, wi).rgb;

上图的积分内部，前边的代表diffuse部分的辐照度，后边代表specular部分的辐照度，本文我们先探讨如何实现diffuse的辐照度。那么我们就可以将积分做如下分解：

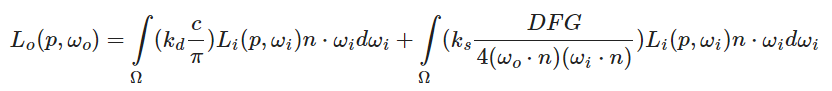
再把第一个积分的常数移出，可得:

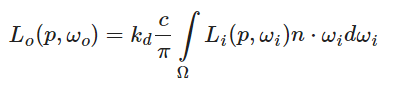
那么计算这个积分其实就比较容易了：给定一个方向n，我们对该方向的半球进行均匀采样，并将采样到的辐照度进行累加积分，重新存储到一张新的贴图中即可，该贴图的每一个像素的坐标都代表了三维空间中的一个方向，像素值则是对该方向所形成的半球的辐照度积分。这张贴图被称作IrradianceMap。下图展示了针对某个方向的积分半球：

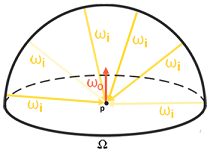
具体求解这个积分可以利用蒙特卡洛方法进行离散化，有两种思路：一种是在球坐标系的空间中针对\(\theta\) 和 \(\phi\)均匀采样，另外一种是利用之前提到过的Cosine-Weighted方法进行采样，两种方法都可以做。我这里采用均匀采样，计算公式如下：


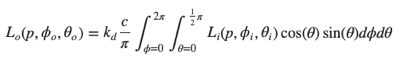
既然是离线计算，CPU和GPU都是可以去做的，这里在shader里实现，代码如下：

float4 PS(VertexOut pin) : SV_Target
{
	float t = (pin.Tex.x - 0.5) * PI * 2.0;
	float p = (pin.Tex.y - 0.5) * PI;
	float3 N = normalize(float3(cos(p) * cos(t), sin(p), cos(p) * sin(t)));
	float3 Nt, Nb;
	if (abs(N.x) > abs(N.y))
		Nt = float3(N.z, 0.0, -N.x);
	else
		Nt = float3(0.0, -N.z, N.y);
	Nt = normalize(Nt);
	Nb = normalize(cross(N, Nt));

	float sampleDelta = 0.025;
	int nSamples = 0;
	float3 irradiance = float3(0.0, 0.0, 0.0);
	for (float phi = 0; phi < PI * 2.0; phi += sampleDelta)
	{
		for (float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
		{
			float3 local_vec = float3(sin(theta) * cos(phi), sin(theta) * sin(phi), cos(theta));
			float3 world_vec = Nt * local_vec.x + Nb * local_vec.y + N * local_vec.z;

			t = atan2(world_vec.z, world_vec.x);
			p = asin(world_vec.y);
			float2 tex_coord = float2((t + PI) / (2.0 * PI), (p + PI * 0.5) / PI);

			irradiance += gEnvironmentMap.Sample(samLinear, tex_coord, 0.0f).rgb * cos(theta) * sin(theta);
			nSamples++;
		}
	}
	irradiance *=  (1.0 / float(nSamples)) * PI;
	
	return float4(irradiance, 1.0);
}

通过以上代码，就可以为EnvrionMentMap生成对应的Diffuse IrradianceMap了。如下图所示：

可以看到比原图模糊了很多。
然后利用生成的IrradianceMap来参与ambient的计算：

float3 fresnelSchlickRoughness(float cosTheta, float3 F0, float roughness)
{
      float minus_rou = 1.0 - roughness;
      return F0 + (max(float3(minus_rou, minus_rou, minus_rou), F0) - F0) * pow(1.0 - cosTheta, 5.0);
}


pin.NormalW = normalize(pin.NormalW);
float theta = atan2(pin.NormalW.z, pin.NormalW.x);	
float phi = asin(pin.NormalW.y);
float3 ks = fresnelSchlickRoughness(max(dot(pin.NormalW, V), 0.0), F0, gMaterial.roughness);
float3 kd = (1.0 - ks) * (1.0 - gMaterial.metallic);
float3 irradiance = gIrradianceMap.Sample(samLinear, getSphericalMapTexCoord(phi, theta), 0.0f).rgb;
float3 diffuse = irradiance * gMaterial.albedo;
float3 ambient = kd * diffuse * ambient_weight;

最终的渲染效果如下图所示，可以看到和直接光照相比变化还不是很明显。之后我们将添加反射积分的间接镜面反射部分，此时我们将真正看到 PBR 的力量。