Cosine-Weighted是一种对球面进行采样的算法，常用于路径追踪时对入射方向进行采样等领域。在介绍该算法之前，我们先来复习一下概率论的知识。
随机变量之间PDF的转换
假设有两个随机变量X和Y，它们的PDF为\(p_x(x)\)和\(p_y(y)\)，假设我们已知\(p_x(x)\)以及Y=f(X)，我们该如何推出\(p_y\)呢？PBRT第13.5小节中给出了推导关系：
\(\LARGE p_y(y)=|\frac{df}{dx}^{-1}| p_x(x)\)
当然前提必须是X和Y是一一对应的转换关系，且\(\frac{df}{dx}\)不能小于0。
举个例子，假设Y=sinX，X采样在[0,1]，且\(p_x(x)=2x\)，那么可得：
\(\LARGE p_y(y)=\frac{2x}{cosx}=\frac{2arcsin y}{\sqrt{1-y^2}}\)
那么如果X和Y是多维的又该如何处理呢？假设X是n维的向量，其中Y=T(X)，且T是双射，那么他们之间的PDF关系如下：
\(\LARGE p_y(y)=\frac{p_x(x)}{|J_T(x)|}\)
其中\(J_T(x)\)是T关于X的雅克比矩阵。
另外，我们在之前的文章中曾经得到：
\(\LARGE d{\omega}=sin{\theta}d{\theta}d{\phi}\)
那么，在围绕球面采样时，因为：
\(\LARGE \int p(\theta, \phi)d\theta d\phi = \int p(\omega)d\omega\)
所以：
\(\LARGE p(\theta, \phi) = sin\theta p(\omega)\)
对球面的采样
当我们获得了一个顶点和它的法向，想去采样得到一个方向时，一般来说有两种针对球面的采样方式：均匀采样方法和Cosine-Weighted采样方法。
均匀采样方法是对球坐标系中的\(\theta\)和\(\phi\)随机采样，理论上所有的方向被采样到的概率都是一样的，均匀采样的PDF c 可以简单计算出：
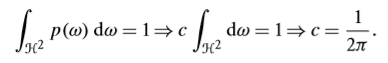
除此之外，我们还可以使用Cosine-Weighted算法来进行采样。
Cosine-Weighted采样指的是立体角方向与竖直方向夹角的余弦值越高，那么该立体角被采样得到的概率就越大的一种采样方式。
我们设\(p(\omega)=c⋅cos\theta\)其中c是常数。
那么我们可以推导出：
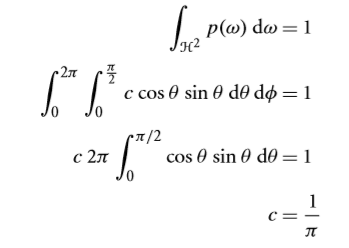
因此\(\large p(\omega)=\frac{cos\theta}{\pi}\),那么\(\large p(\theta, \phi)=\frac{sin\theta cos\theta}{\pi}\)。
得到了概率密度函数后，就可以据此进行采样了。
具体的采样方法其实也非常简单：在顶点所属半球面的截面圆处随机采样一个顶点，然后把它投影到球面上，得到的必然是符合Cosine-Weighted分布的采样：
如何证明这一点呢？在二维圆面上采样可以获得：\(\large p(r,\phi)=\frac{r}{\pi}\)（这个概率密度函数的计算可以见这篇文章中的圆面采样），不难发现 sinθ = r，那么我们可以尝试推导从\(p(r, \phi)\)到\(p(\theta, \phi)\)之间的转换关系。
也就是\(\large (r,\phi)=(sin\theta, \phi) → (\theta, \phi)\)，由此可得雅克比矩阵：
因此：
\(\LARGE p(\theta, \phi)=|J_T|p(r, \phi)=cos\theta \frac{r}{\pi}=\frac{cos\theta sin\theta}{\pi}\)
可以看到和我们前面推导出的\(\large p(\theta, \phi)\)是一模一样的。因此用这种方法采样肯定可以得到符合Cosine-Weighted分布的方向！
