自然语言处理之LSA
LSA(Latent Semantic Analysis), 潜在语义分析。试图利用文档中隐藏的潜在的概念来进行文档分析与检索,能够达到比直接的关键词匹配获得更好的效果。
LSA的核心思想
假设有 nn 篇文档,这些文档中的单词总数为 mm (可以先进行分词、去词根、去停止词操作),我们可以用一个 m∗nm∗n的矩阵 XX 来表示这些文档,这个矩阵的每个元素 XijXij 表示第 ii 个单词在第 jj 篇文档中出现的次数(也可用tf-idf值)。下文例子中得到的矩阵见下图。

LSA试图将原始矩阵降维到一个潜在的概念空间(维度不超过 nn ),然后每个单词或文档都可以用该空间下的一组权值向量(也可认为是坐标)来表示,这些权值反应了与对应的潜在概念的关联程度的强弱。
这个降维是通过对该矩阵进行奇异值分解(SVD, singular value decomposition)做到的,计算其用三个矩阵的乘积表示的等价形式,如下:
\[X=U \Sigma V^{T}
\]
其中 UU 为 m * n 维,ΣΣ 为对角阵 n * n 维,VV 为 n * n 维。
ΣΣ 矩阵中对角线上的每一个值就是SVD过程中得到的奇异值,其大小反映了其对应的潜在概念的重要程度。
然后我们可以自行设定降维后的潜在概念的维度 \(k(k<n)k(k<n)\) , 可以得到:
\[X_{k}=U_{k} \Sigma_{k} V_{k}^{T}
\]
其中 \(U_k\) 是将 \(U\) 仅保留前 \(k\) 列的结果,\(Σk\) 是仅保留前 \(k\) 行及前 \(k\) 列的结果,\(V_k\) 是将 \(V\) 仅保留前 \(k\) 列的结果。
\(X_k\) 则是将 \(X\) 降维到 \(k\) 维的近似结果,这个 \(k\) 越接近 \(n\), \(X_k\) 与 \(X\) 也越接近,但我们的目标并不是越接近越好,LSA认为 \(k\) 值不宜过大(保留了冗余的潜在概念)也不宜过小。
自然语言处理之PLSA
LSA使用线性代数方法,对document-word矩阵进行SVD分解。PLSA则使用了一个概率图模型,引入了一个隐变量topic(可以认为是文档的主题),然后进行统计推断。
为何提出PLSA
在语义分析问题中,存在同义词和一词多义这两个严峻的问题,LSA可以很好的解决同义词问题,却无法妥善处理一词多义问题。
PLSA则可以同时解决同义词和一词多义两个问题。
概率图模型
我们知道文档(一个句子、一个段落或一篇文章)都有它自己的主题,从大的方面讲有经济、政治、文化、体育、音乐、法律、动漫、游戏、法律等等主题,PLSA模型就引入了一个隐变量topic来表示这个主题。
PLSA的概率图模型如下图所示:
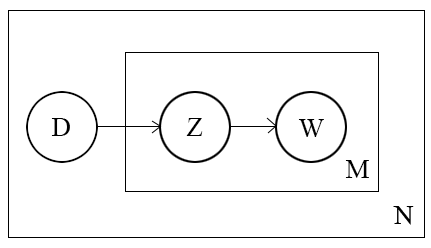
其中 DD 表示文档(document),\(Z\) 表示主题(topic), \(W\) 表示单词(word),其中箭头表示了变量间的依赖关系,比如 \(D\) 指向 \(Z\),表示一篇文档决定了该文档的主题,\(Z\) 指向 \(W\) 表示由该主题生成一个单词,方框右下角的字母表示该方框执行的次数,\(N\) 表示共生成了 \(N\) 篇文档,\(M\) 表示一篇文档按照document-topic分布生成了 \(M\) 次主题,每一次按照生成的主题的topic-word分布生成单词。每个文档的单词数可以不同。
PLSA引入了隐藏变量 \(Z\),认为 \({D,W,Z}{D,W,Z}\) 表示完整的数据集(the complete data set), 而原始的真实数据集 \({D,W}{D,W}\) 是不完整的数据集(incomplete data)。
假设 \(Z\) 的取值共有 \(K\) 个。PLSA模型假设的文档生成过程如下
- 以 \(p(d_i)\) 的概率选择一个文档 \(d_i\)
- 以 \(p(z_k|d_i)\) 的概率选择一个主题 \(z_k\)
- 以 \(p(w_j|z_k)\) 的概率生成一个单词 \(w_j\)
根据图模型,可以得到观测数据的联合分布:
\[\begin{aligned} p\left(d_{i}, w_{j}\right) &=\sum_{k=1}^{K} p\left(d_{i}, w_{j}, z_{k}\right) \\ &=\sum_{k=1}^{K} p\left(d_{i}\right) p\left(z_{k} | d_{i}\right) p\left(w_{j} | z_{k}\right) \\ &=p\left(d_{i}\right) \sum_{k=1}^{K} p\left(z_{k} | d_{i}\right) p\left(w_{j} | z_{k}\right) \end{aligned}
\]
第一个等式是对三者的联合概率分布对其中的隐藏变量 \(Z\) 的所有取值累加,第二个等式根据图模型的依赖关系将联合概率展开为条件概率,第三个等式只是简单的乘法结合律。这样就计算出了第 \(i\) 篇文档与第 \(j\) 个单词的联合概率分布。
我们可以得到完整数据的对数似然为:
\[\begin{aligned} L &=\sum_{i=1}^{N} \sum_{j=1}^{M} n\left(d_{i}, w_{j}\right) \log \left(p\left(d_{i}, w_{j}\right)\right) \\ &=\sum_{i=1}^{N} \sum_{j=1}^{M} n\left(d_{i}, w_{j}\right) \log \left(p\left(d_{i}\right) \sum_{k=1}^{K} p\left(z_{k} | d_{i}\right) p\left(w_{j} | z_{k}\right)\right) \\ &=\sum_{i=1}^{N} n\left(d_{i}\right) \log \left(p\left(d_{i}\right)\right)+\sum_{i=1}^{N} \sum_{j=1}^{M} n\left(d_{i}, w_{j}\right) \log \sum_{k=1}^{K} p\left(z_{k} | d_{i}\right) p\left(w_{j} | z_{k}\right) \end{aligned}
\]
\(p(z_k|d_i)\) 和 \(p(w_j|z_k)\) 是PLSA模型需要求解的参数,
使用EM求解PLSA
可以看之前所写的关于EM 算法的blog,对于其中的函数 \(Q\), 现在给出PLSA中 \(Q\) 函数的形式
\[\begin{aligned} Q\left(\theta, \theta^{o l d}\right) &=\sum_{i=1}^{N} \sum_{j=1}^{M} n\left(d_{i}, w_{j}\right) \sum_{k=1}^{K} p\left(z_{k} | d_{i}, w_{j}\right) \log p\left(d_{i}, w_{j}, z_{k} ; \theta\right) \\ &=\sum_{i=1}^{N} \sum_{j=1}^{M} n\left(d_{i}, w_{j}\right) \sum_{k=1}^{K} p\left(z_{k} | d_{i}, w_{j}\right) \log \left[p\left(d_{i}\right) p\left(z_{k} | d_{i}\right) p\left(w_{j} | z_{k}\right)\right] \end{aligned}
\]
注意到这是因为如前文所说,在本问题中,认为\({D,W,Z}\) 是完整的数据集。
由于 \(p(d_i)∝n(d_i) ,\) 表示第 \(i\) 篇文档的单词总数,这一项估计并不重要,因此上式去掉该项,得到:
\[Q\left(\theta, \theta^{o l d}\right)=\sum_{i=1}^{N} \sum_{j=1}^{M} n\left(d_{i}, w_{j}\right) \sum_{k=1}^{K} p\left(z_{k} | d_{i}, w_{j}\right) \log \left[p\left(z_{k} | d_{i}\right) p\left(w_{j} | z_{k}\right)\right]
\]
可以看到对数中是参数的乘积,不再包含求和的部分。
我们注意到,参数存在下面的两个约束:
\[\begin{array}{l}{\sum_{j=1}^{M} p\left(w_{j} | z_{k}\right)=1} \\ {\sum_{k=1}^{K} p\left(z_{k} | d_{i}\right)=1}\end{array}
\]
因此可以使用拉格朗日乘子法(Lagrange multiplier)求取使得 \(Q\) 函数最大时对应的参数。
写出拉格朗日函数:
\[Lagrange=Q+\sum_{k=1}^{K} \tau_{k}\left(1-\sum_{j=1}^{M} p\left(w_{j} | z_{k}\right)\right)+\sum_{i=1}^{N} \rho_{i}\left(1-\sum_{k=1}^{K} p\left(z_{k} | d_{i}\right)\right)
\]
对拉格朗日函数中的 \(p(w_j|z_k)\) 求偏导,令其等于零,得到:
\[\sum_{i=1}^{N} n\left(d_{i}, w_{j}\right) p\left(z_{k} | d_{i}, w_{j}\right)-\tau_{k} p\left(w_{j} | z_{k}\right)=0,1 \leq j \leq M, 1 \leq k \leq K
\]
对该式 \(1≤k≤K\) 所有取值下等式两边累加,可以消去 \(p(z_{k}|d_i)\), 从而得到 \(ρ_i\) 的表达式,回带到上式得到下式:
\[p\left(z_{k} | d_{i}\right)=\frac{\sum_{j=1}^{M} n\left(d_{i}, w_{j}\right) p\left(z_{k} | d_{i}, w_{j}\right)}{n\left(d_{i}\right)}
\]
这样就得到了EM算法的M-Step重新估计参数的公式。
那么在E-Step如何计算 \(z\) 的后验概率呢?根据下式计算,第一个等式是贝叶斯法则,第二个等式是根据图模型将联合概率展开,第三个等式是分子分母同时除以一个因子。
\[\begin{aligned} p\left(z_{k} | d_{i}, w_{j}\right) &=\frac{p\left(d_{i}, w_{j}, z_{k}\right)}{p\left(d_{i}, w_{j}\right)} \\ &=\frac{p\left(d_{i}\right) p\left(z_{k} | d_{i}\right) p\left(w_{j} | z_{k}\right)}{\sum_{l=1}^{K} p\left(d_{i}\right) p\left(z_{l} | d_{i}\right) p\left(w_{j} | z_{l}\right)} \\ &=\frac{p\left(z_{k} | d_{i}\right) p\left(w_{j} | z_{k}\right)}{\sum_{l=1}^{K} p\left(z_{l} | d_{i}\right) p\left(w_{j} | z_{l}\right)} \end{aligned}
\]
自然语言处理之LDA
我们知道,PLSA也定义了一个概率图模型,假设了数据的生成过程,但是不是一个完全的生成过程:没有给出先验。因此PLSA给出的是一个最大似然估计(ML)或者最大后验估计(MAP)。
LDA拓展了PLSA,定义了先验,因此LDA给出的是一个完整的贝叶斯估计。
这里先给出本文公式中以及python代码中使用到的符号及其含义。关于编号,公式中从1开始编号,代码中从0开始编号,只是为了方便。
LDA 的生成过程:
对于所有的主题 \(\mathrm{k} \in[1, \mathrm{K}]\), do
样本混合元素:\(\overrightarrow{\varphi_{k}} \sim \operatorname{Dir}(\vec{\beta})\)
队友所有的文本 \(\mathrm{i} \in[1, \mathrm{N}]\):
样本混合的比例:\(\overrightarrow{\theta_{i}} \sim \operatorname{Dir}(\vec{\alpha})\)
样本混合的长度:\(N_{i} \sim \operatorname{Poiss}(\xi)\)
对于所有的元素:\(j \in\left[1, \mathrm{N}_{i}\right]\) 在文本 \(i\) 中:
样本主题的标签:\(z_{i, j} \sim \operatorname{Mult}\left(\overrightarrow{\theta_{i}}\right)\)
样本单词的类别:\(w_{i, j} \sim M u l t\left(\overrightarrow{\varphi_{z_{i, j}}}\right)\)
由该生成过程以及dirichlet-multinomial共轭可得:
\[\begin{array}{l}{p(\vec{z} | \vec{\alpha})=\prod_{i=1}^{N} \frac{\Delta\left(\overrightarrow{n_{i}}+\vec{\alpha}\right)}{\Delta(\vec{\alpha})}} \\\\ {p(\vec{w} | \vec{z}, \vec{\beta})=\prod_{z=1}^{K} \frac{\Delta\left(\overrightarrow{n_{z}}+\vec{\beta}\right)}{\Delta(\vec{\beta})}}\end{array} \\
\]
\[\begin{aligned} p(\vec{w}, \vec{z} | \vec{\alpha}, \vec{\beta}) &=p(\vec{w} | \vec{z}, \vec{\beta}) p(\vec{z} | \vec{\alpha}) \\ &=\prod_{z=1}^{K} \frac{\Delta\left(\vec{n}_{z}+\vec{\beta}\right)}{\Delta(\vec{\beta})} \prod_{i=1}^{N} \frac{\Delta\left(\overrightarrow{n_{i}}+\vec{\alpha}\right)}{\Delta(\vec{\alpha})} \end{aligned}
\]
根据上面的概率图模型,可以得出第i篇文档的complete-data似然性为:
\[p\left(\vec{w}_{i}, \vec{z}_{i}, \overrightarrow{\theta_{i}}, \Phi | \vec{\alpha}, \vec{\beta}\right)=\prod_{j=1}^{N_{i}} p\left(w_{i, j} | \overrightarrow{\varphi_{z_{i j}}}\right) p\left(z_{i, j} | \overrightarrow{\theta_{i}}\right) \cdot p\left(\overrightarrow{\theta_{i}} | \vec{\alpha}\right) \cdot p(\Phi | \vec{\beta})
\]
第i篇文档第j个单词在词表中编号为w的概率为:
\[p\left(w_{i, j}=w | \overrightarrow{\theta_{i}}, \Phi\right)=\sum_{k=1}^{K} p\left(w_{i, j}=w | \overrightarrow{\varphi_{k}}\right) p\left(z_{i, j}=k | \overrightarrow{\theta_{i}}\right)
\]
整个数据集的似然性为:
\[p(\mathcal{D} | \Theta, \Phi)=\prod_{i=1}^{N} p\left(\overrightarrow{w_{i}} | \overrightarrow{\theta_{i}}, \Phi\right)=\prod_{i=1}^{N} \prod_{j=1}^{N_{i}} p\left(w_{i, j} | \overrightarrow{\theta_{i}}, \Phi\right)
\]
PLSA中的概率图模型由于没有先验,模型比LDA简单一些,认为文档决定topic,topic决定单词,写出了整个数据集的对数似然性,然后由于要求解的参数以求和的形式出现在了对数函数中,无法通过直接求导使用梯度下降或牛顿法来使得这个对数似然最大,因此使用了EM算法。
LDA同样可以使用EM算法求解参数,但需要在E步计算隐变量的后验概率时使用变分推断进行近似,一种更简单的方法是使用gibbs sampling。
gibbs sampling
这部分的公式推导如下:
\[p\left(z_{l}=z | \overrightarrow{z_{l}-l}, \vec{w}\right)=\frac{p(\vec{w}, \vec{z})}{p\left(\vec{w}, \vec{z}_{\neg l}\right)} \\\\ =\frac{p(\vec{w} | \vec{z}) p(\vec{z})}{p\left(\vec{w}_{l} | \vec{z}_{l}\right) p\left(w_{l}\right) p\left(\vec{z}_{l}\right)} \propto \frac{p(\vec{w} | \vec{z}) p(\vec{z})}{p\left(\vec{w}_{\eta} | \overrightarrow{z_{\eta}}\right) p\left(\overrightarrow{z_{\eta}}\right)} \\\\ =\frac{\Delta\left(\overrightarrow{n_{i}}+\vec{\alpha}\right)}{\Delta\left(n_{i, l}+\vec{\alpha}\right)} \cdot \frac{\Delta\left(\overrightarrow{n_{z}}+\vec{\beta}\right)}{\Delta\left(\overrightarrow{n_{z}, \eta}+\vec{\beta}\right)} \\\\ =\frac{\Gamma\left(n_{i z}+\alpha_{z}\right) \Gamma\left(\sum_{z=1}^{K}\left(n_{i z, \eta}+\alpha_{z}\right)\right)}{\Gamma\left(n_{i z, \eta}+\alpha_{z}\right) \Gamma\left(\sum_{z=1}^{K}\left(n_{i z}+\alpha_{z}\right)\right)} \cdot \frac{\Gamma\left(n_{z w}+\beta_{w}\right) \Gamma\left(\sum_{w=1}^{M}\left(n_{z w, l}+\beta_{w}\right)\right)}{\Gamma\left(n_{z w, \eta}+\beta_{w}\right) \Gamma\left(\sum_{w=1}^{M}\left(n_{z w}+\beta_{w )}\right)\right.}\\\\=\frac{n_{i z, 7 l}+\alpha_{z}}{\sum_{z=1}^{K}\left(n_{i z, 7 l}+\alpha_{z}\right)} \cdot \frac{n_{z w, l}+\beta_{w}}{\sum_{w=1}^{M}\left(n_{z w, 7}+\beta_{w}\right)}\propto \frac{n_{z w, 7 l}+\beta_{w}}{\sum_{w=1}^{M}\left(n_{z w, 7}+\beta_{w}\right)} \cdot\left(n_{i z, 7 l}+\alpha_{z}\right)\\\\=\frac{n z w[z, w]}{n z[z]} \cdot(n d z[i, z])
\]
下面解释一下这个推导过程,前两个等号是利用了贝叶斯公式,第三步的正比于符号这一行是去掉了一项常数 \(p(w_l)\),第四步利用了前面计算好的 \(p(\vec{w}, \vec{z})\) 联合概率公式,第五、六步是将函数展开并化简,第七步的正比于符号是去掉了一项不依赖于z的项(即z取何值该项都相同),最后一行给出了对应代码中的表达。
这样我们就得到了吉布斯采样公式,每一轮gibbs sampling的迭代中依次遍历每个二维下标 ll, 即遍历每篇文档的每一个单词,重新采样这个下标对应的topic编号。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号