Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China

Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China

• Published In SCIENCE Volume 368 | Issue 6492 15 May 2020
• Total Citations ： 267
• Date: 15 May 2020
• DOI: 10.1126/science.abb4557
• Data and materials availability: Both the data and analysis material are available online at Zenodo

Abstract:

The recent outbreak of coronavirus disease 2019 (COVID-19) in mainland China was characterized by a distinctive subexponential increase of confirmed cases during the early phase of the epidemic, contrasting with an initial exponential growth expected for an unconstrained outbreak. We show that this effect can be explained as a direct consequence of containment policies that effectively deplete the susceptible population. To this end, we introduce a parsimonious model that captures both quarantine of symptomatic infected individuals, as well as population-wide isolation practices in response to containment policies or behavioral changes, and show that the model captures the observed growth behavior accurately. The insights provided here may aid the careful implementation of containment strategies for ongoing secondary outbreaks of COVID-19 or similar future outbreaks of other emergent infectious diseases.
中国大陆最近爆发的2019冠状病毒病(COVID-19)的特点是，在疫情初期，确诊病例明显呈亚指数增长，而不是预期的无约束爆发时的指数增长.我们表明，这种影响可以解释为有效地耗尽易感人群的遏制政策的直接后果。为此，我们引入了一个简单的模型，该模型既捕捉了有症状的感染者的隔离，也捕捉了应对遏制政策或行为变化的人群范围内的隔离做法，并表明该模型准确地捕捉了观察到的生长行为， 本文提供的见解可能有助于仔细实施遏制战略，以应对正在发生的COVID-19二次暴发或未来类似的其他突发传染病暴发。

Model

To test the hypothesis that the observed growth behavior can be caused by mitigation policies that apply to both infected and susceptible individuals.
we extend the SIR model by two additional mechanisms, one of which can be
interpreted as a process of removing susceptibles from the transmission process: First, we assume that general public containment efforts or individual behavioral changes in response to the epidemic effectively remove individuals from the interaction dynamics or significantly reduce their participation in the transmission dynamics. We will refer to this mechanism as “containment” in the following.
Second, we account for the removal of symptomatic infected individuals, which we will refer to as “quarantine” procedures.
检验观察到的生长行为可能由适用于受感染和易感个体的缓解政策引起的假设。
我们通过两个附加机制扩展了SIR模型，其中一个机制可以是被解释为从传播过程中消除易感因素的过程：首先，我们假设一般的公共遏制措施或个人行为改变有效地将个人从互动动态中移除，或显著减少他们在传播动态中的参与。在下文中，我们将这种机制称为“遏制”。
第二，我们考虑清除有症状的感染者，我们称之为“隔离”程序。

a generalization of the standard SIR model, henceforth referred to as the **SIR-X ** model.标准SIR模型的一般化，此后称为SIR- x模型。

The rate parameters α and β quantify the transmission rate and the recovery rate of the standard SIR model, respectively. Additionally,the impact of containment efforts is captured by the terms proportional to the containment rate k0 that is effective in both I and S populations, because measures such as social distancing and curfews affect the whole population alike. Infected individuals are removed at rate k corresponding to quarantine measures that only affect symptomatic infecteds.
The new compartment X quantifies symptomatic, quarantined infecteds. Here we assume that the fraction X(t) is proportional to the empirically confirmed and reported cases C(t) and that the time period between sampling and test results can be neglected. The case k0 = 0 corresponds to a scenario in which the general population is unaffected by policies or does not commit behavioral changes in response to an epidemic. The case k0 = 0 corresponds to a scenario in which symptomatic infecteds are not isolated specifically.

速率参数 α and β 分别量化了标准 SIR 模型的传播速率和恢复速率。此外，遏制努力的影响可以用与遏制率 k0成比例的术语来表示，k0对 i 型和 s 型人口都有效，因为社会距离和宵禁等措施对整个人口都有同样的影响。感染者被清除的速度为 k，相当于只影响有症状感染者的隔离措施。
新的隔离室 x 量化了有症状的隔离感染者。在这里，我们假设分数 x (t)与经验确认和报告的案例 c (t)成正比，并且可以忽略抽样和检验结果之间的时间间隔。K0 = 0的情况对应于一种情况，在这种情况下，一般人口不受政策的影响，或者不对流行病作出行为变化的反应。K0 = 0的情况与有症状的感染者不是特别孤立的情况相对应。

In the basic SIR model that captures unconstrained, free spread of the disease, the basicreproduction number R0 is related to transmission and recovery rate by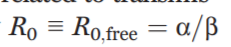
because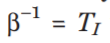is the average time an infected individual remains infectious before
recovery or removal. Here, the time period
that an infected individual remains infectious is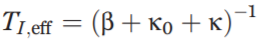such that theeffective, or “observed,” reproduction number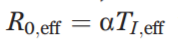is smaller than R0;free because both k0 > 0 and k > 0.

The key mechanism at work in the model defined by Eqs. 1 to 4 is the exponentially fast depletion of susceptibles in addition to isolation of infecteds. This effect is sufficient to account for the observed scaling law in the number of confirmed cases for a plausible range of model parameters as discussed below
在方程式1至4所定义的模型中起作用的关键机制是除隔离受感染者外，易感者的指数快速耗竭。这种效应足以解释如下所述的模型参数的合理范围内，在已确认的案例数中观察到的标度律

Conclusion

The model reproduces the empirical case counts in all provinces well for plausible parameter values. The quality of the reproduction of the case counts in all 29 affected provinces can be used to estimate the peak time of the number of asymptomatic or oligosymptomatic infected individuals in the population, which is the key quantity for estimating the time when an outbreak will wane.
该模型较好地再现了各省份的经验案例数，得到了合理的参数值。在所有29个受影响省份中，病例计数的复制质量可用于估计人口中无症状或少症状感染者人数的高峰时间，这是估计疫情消退时间的关键数量

We stress that our model describes the general effects of containment mechanisms, effectively averaged over many applied strategies or individual changes of behavior. Our analysis therefore cannot identify the efficacy of specific actions. As the implementation of drastic measures such as mandatory curfews can have severe consequences for both individuals as well as a country’s society and economy, decisions about their application should not be made lightly.
我们强调，我们的模型描述了遏制机制的一般影响，有效地平均了许多应用策略或行为的个人变化。因此，我们的分析不能确定具体行动的有效性。由于强制宵禁等严厉措施的实施可能对个人以及一个国家的社会和经济产生严重后果，因此不应轻率地决定是否实施这些措施。