单源最短路径算法之bellman-ford

单源最短路径算法之 \(bellman-ford\)

1. 以边为研究对象
2. 单起点多终
3. 允许有负边权

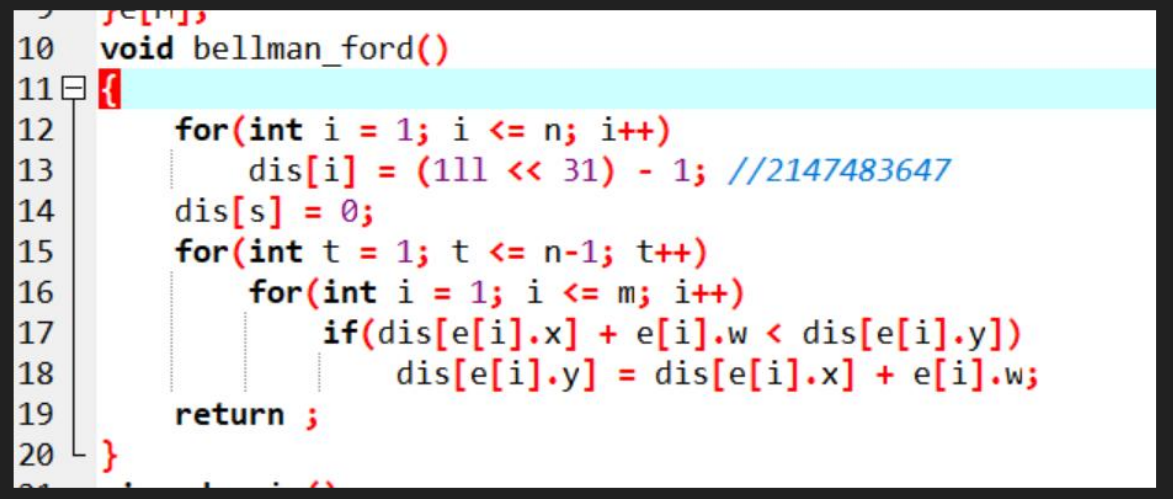
\(bellman-ford\) 的工作原理

假设 \(n\) 个点 \(m\) 条有向边的图，求 \(s\) 为起点的最短路

条以 \(s\) 出发的最短路，最多包含 \(n\) 个点，\(n-1\) 条边

对于一条边 \((x,y,w)\)，\(y\) 可能被 \(x\) 松弛，若最短路需要更新，那么 \(m\) 条边中至少会有 \(1\) 条松弛成功

重复枚举 \(m\) 条边进行松弛，\(n-1\) 轮之后一定能够松弛完毕。

时间复杂度：\(O(nm)\)

\(bellman-Ford\) 算法的队列优化（\(SPFA\)，\(Shortest\ Path\ Faster\ Algorithm\)）

每一轮枚举条边太慢了，注意到对于点 \(x\)，只有被松弛成功后，\(x\) 的出边才可能松弛成功

维护队列 \(q\)，存储被松弛成功的点，注意点 \(x\) 可能被松弛多次，因此会进出队多次

单源最短路径，边权一样跑 \(DFS\)，边权为正数跑 \(Dijkstra\) ，边权为负数跑 \(SPFA\)