特殊的数

目录

• 特殊的数
• 卡特兰数
  • 定义
• 斯特林数
  • 第二类斯特林数
    • 定义 :
    • 递推式：
    • 通项公式：
  • 第一类斯特林数
    • 定义：
    • 递推式：
    • 递推边界以及特殊值：
      • 两种斯特林数的大小关系：
    • 定理
  • 斯特林数与三种幂(很重要！)
    • • 下降幂
      • 上升幂
      • 相关结论
    • 上升下降幂与普通幂的转换
    • 反转公式
    • 斯特林反转
    • 总结一下：
  • 斯特林数与生成函数
    • 补充
• 伯努利数
• 欧拉数
  • 推导欧拉数·行的生成函数
• 分拆数
  • • 五边形数定理
    • Ferrers 图（又称杨表）

特殊的数

前言：

我之前是对每个特殊的数都各开一个博客的，但是这些数用生成函数的视角下看，似乎有一些关系，感觉分开写就太杂了，于是我把这些特殊的数整合到了一起。

卡特兰数

定义

\(Catalan\) 数列 \(H_n\) 是以下问题的方案数：

• 有一个大小为 \(n × n\) 的方格图，左下角为 \((0, 0)\) 右上角为 \((n, n)\)，从左下角开始 每次都只能向右或者向上走一单位，不走到对角线 \(y = x\) 上方（但可以触碰） 的情况下到达右上角有多少可能的路径？
• 在圆上选择 \(2n\) 个点，将这些点成对连接起来使得所得到的 \(n\) 条线段不相交的 方法数？
• 一个栈的进栈序列为 \(1, 2, 3, · · · , n\) 有多少个不同的出栈序列？
• \(n\) 个结点可构造多少个不同的二叉树？
• \(n\) 对括号能组成的括号序列数？
• ......

这些问题的方案数可以证明是相等的。我们先以第一个命题来具体研究 \(Catalan\) 数

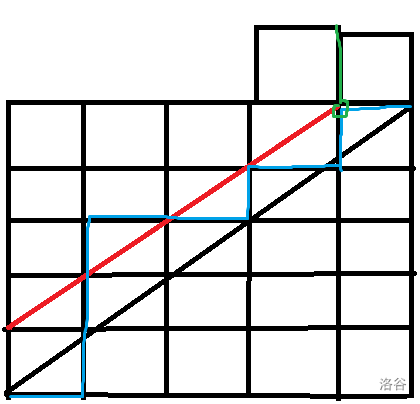
图片有点抽象还请各位海涵一下。

我们从（1，1）走到（n，n）的方案数可以递推来求。

设我们第一次接触到对角线时的横坐标为i，前面的方案数可看为从（2，1）走到（i，i-1）的方案数，后面的方案数可看为从（i，i）走到（n,n）的方案数。

对 \(i\) 求和有：\(H_n = \sum^{n}_{i=1}H_{i-1}H_{n-i}\)，这就是卡特兰数的递推式。初值为 \(H_0 = 1\)。

我们还可以看为总方案数减去超过对角线（触碰到红线）的方案数。

我们对最后一次触碰到红线后的部分进行翻转，则原来的每一条不合法路径（如蓝色）就一一对应了一条终点为（n-1，n+1）的路径(如绿色)。

所以卡特兰数的组合意义是 \(H_n = {2n \choose n} - {2n \choose n-1}\)。

综上：

\[H_n = \begin{cases} \sum_{i = 0}^{n - 1} H_iH_{n - i - 1} & (n\geq2) \\ 1 & (n = 0,1) \end{cases}\\ H_n = \binom{2n}{n}-\binom{2n}{n - 1} \]

再看卡特兰数的第二个和第四个定义，可以发现它们的递推式与该递推式相同。对于第三个和第五个定义，可以认为就是在走网格，并且横向步数不超过纵向步数。

生成函数：\(\dfrac{H(x)-1}x =H^2(x) \Rightarrow H(x)=\dfrac{1-\sqrt{1-4x}}{2x}\)

可以推导出 \(\sum_n\dbinom {2n}n x^n = \sqrt{(1-4x)}\).

通项公式：\(H_n = \dfrac{\binom{2n}{n}}{n + 1}\)。这个使用递推公式的生成函数搞出来的，证明比较麻烦，这里不再赘述 。你也可以把该式子带入组合意义中来验证其正确性。

递推式2：\(H_n = \dfrac{H_{n - 1}(4n - 2)}{n + 1}\) ，这个可以直接带入验证。

因为上课讲的例题都没怎么听懂，这里就不放题了。

斯特林数

第二类斯特林数

定义 :

\(n \brace m\) 表示将n个有标号数放在m个非空无标号集合的方案数（注：斯特林数写作大括号）

递推式：

\[{n \brace m} = {n - 1 \brace m - 1} + m \times{n - 1 \brace m} \]

其组合意义是：把最后一个数单开一列 \({n - 1 \brace m - 1}\) 加上把最后一个数放入 \(m\) 个集合中的其中一个 \(m \times{n - 1 \brace m}\)

递推边界：${n\brace n} = {n \brace 1} = 1(n \ge 0) $， \({n \brace 0} = [n = 0]\)

还有其他一些特值: \(\ \begin{array}{l} \left\{\begin{matrix}n\\2\end{matrix}\right\}=2^{n - 1}-1(n>0), \left\{\begin{matrix}n\\n - 1\end{matrix}\right\}=\binom{n}{2} \end{array} \)

通项公式：

\[{n \brace m} = \sum_{i=0}^m\frac{i^n\cdot(-1)^{m-i}}{(m-i)!i!} \]

证明：设将 n 个有标号物品放到 k 个有标号盒子（允许空盒子）的方案数为 \(G_k\)；将 n 个有标号物品放到 k 个有标号盒子（不允许空盒子）的方案数为 \(F_k\)

\[\therefore G_k = k^n, G_k = \sum^k_{i=0} \binom ki F_i \]

第二个式子表示从 n 个盒子选 i 个必须放物品，然后对 i 求和。

然后二项式反演，得到：

\[F_k = \sum^k_{i=0}(-1)^{k-i}\binom kiG_i = \sum^k_{i=0}(-1)^{k-i}\binom ki k^n \]

因为 \(F\) 的物品有标号，所以 :

\[{F_k\over n!} = {n \brace k} \]

带回去就得到：

\[{n \brace m} = \sum_{i=0}^m\frac{i^n\cdot(-1)^{m-i}}{(m-i)!i!} \]

例题 P5162 WD与积木 - 洛谷

题意 : 把\(1...n\)分割成若干个集合,集合之间有顺序,问所有不同的分割方法之中,集合个数的期望。

相当于求 \(\dfrac{\sum_i{n\brace i}i!i}{\sum_i{n\brace i}i!}\) .

对于分母：

\[\begin{aligned}&\sum_{n\geq 0}\frac{x^n}{n!}\sum_{i=0}^n\begin{Bmatrix}n\\i\end{Bmatrix}i!\\=&\sum_{i\geq 0}i!\sum_{n\geq 0}\frac{x^n}{n!}\begin{Bmatrix}n\\i\end{Bmatrix}\\=&\sum_{i\geq 0}\sum_{n\geq 0}\frac{x^n}{n!}\sum_{k=0}^i(-1)^k\binom{i}{k}(i-k)^n\\=&\sum_{i\geq 0}\sum_{k=0}^i(-1)^{i-k}\binom{i}{k}\sum_{n\geq 0}\frac{(kx)^n}{n!}\\=&\sum_{i\geq 0}\sum_{k=0}^i(-1)^{i-k}\binom{i}{k}(e^x)^k\\=&\sum_{i\geq 0}(e^x-1)^i\\=&\frac{1}{2-e^x}\end{aligned} \]

对于分子：

\[\begin{aligned}&\ \ \sum_{n\geq 0}\frac{x^n}{n!}\sum_i{n\brace i}i!i \\&=\sum_{i\geq 0}i(e^x-1)^i\\ &=\sum_{i\geq 0}\sum_{j=1}^i(e^x-1)^i\\ &=\sum_{j=1}^n\sum_{i}(e^x-1)^{i+j}\\ &=\sum_{j=1}^n(e^x-1)^{j}\sum_{i}(e^x-1)^{i}\\ &=\frac{1}{2-e^x}\sum_{j=1}^n(e^x-1)^{j}\\ &=\frac{1-e^x}{(2-e^x)}\sum_{j=0}^n(e^x-1)^{j}\\ &=\frac{1-e^x}{(2-e^x)^2}\\ \end{aligned} \]

分子分母取 n 次项系数后相除即可。

第一类斯特林数

定义：

\(n \brack m\)：表示将 n 个元素排成 m 个轮换的方案数。也即所有 n! 个排列中，构成的置换有 m 个无标号环的排列数。

递推式：

\[{n\brack m} = {n-1\brack m-1} + (n-1){n-1\brack m} \]

其组合意义是：考虑最后一个元素，可以加入任意一个轮换并且可以插入任意一个位置，相当于可以任选一个数，插在其后面 \((n-1){n-1\brack m}\)，也可以新开一个轮换 \({n-1\brack m-1}\)。

递推边界以及特殊值：

\[{n\brack 0} = [n = 0], {n \brack n} = 1\\ {n\brack 1} = (n-1)!, {n\brack n-1} = {n \choose 2} \]

两种斯特林数的大小关系：

由定义和递推式容易看出 ：\({n \brace m} \le {n \brack m}\)。当 m 等于 n，n-1，0 时等号成立。

定理

我们知道一个有 n 个元素的排列和一个 n 个元素的置换一一对应，于是对所有置换 中的轮换个数求和，我们有:

\[\sum_{k = 0}^{n}\begin{bmatrix}n\\k\end{bmatrix}=n! \]

斯特林数与三种幂(很重要！)

先复习一下上升幂，下降幂：

下降幂

\(n^{\underline{m}}=n(n - 1)(n - 2)\cdots(n - m + 1)\)

上升幂

\(n^{\overline{m}}=n(n + 1)(n + 2)\cdots(n + m - 1)\)

相关结论

1. \(n^{\overline{m}}=(n + m - 1)^{\underline{m}}\)，用于处理上升幂
2. \(n^{\underline{m}}=(n - m + 1)^{\underline{m}}\)，用于处理 \(n < 0\) 情况
3. \(x^{\underline{n}}=(-1)^{n}(-x)^{\overline{n}}\)，用于上升下降幂的转换
4. \(\binom{n}{m}=\frac{n^{\underline{m}}}{m!}\)

上升下降幂与普通幂的转换

注意到，上升幂和下降幂本质上也是多项式，所以一个多项式也可以用上升幂和下降幂来表示。

他们的关系如下：

\[x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\underline{k}}=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}\binom{x}{k}k!\\ x^{\overline n} = \sum^n_{k=0}{n\brack k}x^k \]

可以简记为第二类斯特林数对应下降幂，第一类斯特林数对应上升幂

因为下降幂的组合意义比上升幂更好，所以更常用第一个式子来转换普通幂

对于第一个式子，考虑组合意义证明：

\(x^n\) 表示 x 个有标号盒子放 n 个有标号球的方案数，盒子可以为空。

现在枚举非空盒子数 i，先从 x 个盒子里面选 i 个盒子，\(\dbinom xi\)，

然后发现第二类斯特林数的定义是把 n 个球放入 i 个无标号盒子的方案数，

注意到这里的盒子是有标号的，所以 \({n\brace i}i!\) 就是有标号球放到有标号盒子的数量，所以：(个人感觉这里和第二类斯特林的通项公式证明几乎一致)

\[x^n = \sum_i^n {n\brace i}\dbinom xi i!= \sum_i^n {n\brace i}x^\underline i \]

当然也可以使用数学归纳法证明第一个式子：

首先观察到：\(x^{\underline{k + 1}}=x^{\underline{k}}(x - k)\Longrightarrow x\cdot x^{\underline{k}}=x^{\underline{k + 1}}+kx^{\underline{k}}\)。

那么：

\[\begin{align*} x\cdot x^{n - 1}&=x\cdot\sum_{k = 0}^{n - 1}\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}x^{\underline{k}}\\ &=\sum_{k = 0}^{n - 1}\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}x^{\underline{k+1}}+\sum_{k = 0}^{n - 1}\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}kx^{\underline{k}}\\ &=\sum_{k = 1}^{n}\left\{\begin{matrix}n - 1\\k - 1\end{matrix}\right\}x^{\underline{k}}+\sum_{k = 1}^{n - 1}\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}kx^{\underline{k}}\\ &=\sum_{k = 1}^{n}\left(k\left\{\begin{matrix}n - 1\\k\end{matrix}\right\}+\left\{\begin{matrix}n - 1\\k - 1\end{matrix}\right\}\right)x^{\underline{k}}\\ &=\sum_{k = 1}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\underline{k}} \end{align*} \]

第二个式子也可以用数学归纳法证明：

不过这次的观察是 : \((x+n-1) \cdot x^{k}=x^{k+1}+(n-1) x^{k}\)

\[\begin{aligned} x^{\overline n} & =(x+n-1) x^{\overline{n-1}} \\ & =(x+n-1) \sum_{k=0}^{n-1}\left[\begin{array}{c} n-1 \\ k \end{array}\right] x^{k} \\ & =\sum_{k=0}^{n-1}(n-1)\left[\begin{array}{c} n-1 \\ k \end{array}\right] x^{k}+\sum_{k=1}^{n}\left[\begin{array}{l} n-1 \\ k-1 \end{array}\right] x^{k} \\ & =\sum_{k=0}^{n}\left[\begin{array}{l} n \\ k \end{array}\right] x^{k} \end{aligned} \]

观察到，注意到上升幂和下降幂的多项式展开后，系数是有交错的符号，比如：

\[\begin{align*} x^{\underline{4}}&=x(x - 1)(x - 2)(x - 3)=x^{4}-6x^{3}+11x^{2}-6x\\ x^{\overline{4}}&=x(x + 1)(x + 2)(x + 3)=x^{4}+6x^{3}+11x^{2}+6x \end{align*} \]

形式化的表示为：

\[\begin{aligned} & x^{\overline{n}}=\sum_{k = 0}^{n}\left[\begin{array}{l}n\\k\end{array}\right]x^{k}\\ & x^{\overline{n}}=\sum_{k = 0}^{n}(-1)^{n-k}\left[\begin{array}{l}n\\k\end{array}\right]x^{k} \end{aligned} \]

由

\[x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\underline{k}} \]

和

\[x^{\underline{n}}=(-1)^{n}(-x)^{\overline{n}} \]

得到：

\[x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}(-1)^k(- x)^{\overline{k}} \]

用 \(-x\) 替换 \(x\)，然后合并 \(-1\) 的系数后易得：

\[x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}(-1)^{n-k}x^{\overline{k}} \]

推论 : \(\sum\limits_{i=0}^ni^k=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{n+1}{j+1}\) (设\(0^0=1\))

左边 \(=\sum\limits_{i=0}^n\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{i}{j}\)

\(=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\sum\limits_{i=0}^n\dbinom{i}{j}\)

\(=\sum\limits_{j=0}^m\begin{Bmatrix}k \\ j\end{Bmatrix}*j!*\dbinom{n+1}{j+1}\)

反转公式

由上总结，我们能感受到两类斯特林数密不可分的关系，接下来我们就来探究它们的关系。

我们把普通幂转上升幂再转普通幂得：

\[x^n=\sum^n_{j=0}\sum_{k = j}^{n}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}{k\brack j}x^j \]

把 \(\sum_{k = j}^{n}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}{k\brack j}\) 作为 \(x^j\)的系数，只有 \(j = n\) 时右边的系数为1，其余的系数为0。

所以得到第一个反转公式：

\[\sum_{k = j}^{n}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}{k\brack j} = [j = n] \]

\[\because \left\{\begin{matrix}n\\n\end{matrix}\right\}{n\brack n} = 1\\ \therefore \sum_{k = j}^{n-1}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}{k\brack j} = 0 \]

同理我们把普通幂转下降幂再转普通幂得：

\[\sum_{k=m}^{n}\left[\begin{array}{l}n\\k\end{array}\right]\left\{\begin{array}{l}k\\m\end{array}\right\}(-1)^{n - k}=[m = n] \]

\[\sum_{k=m}^{n}\left\{\begin{array}{l}n\\k\end{array}\right\}\left[\begin{array}{l}k\\m\end{array}\right](-1)^{n - k}=[m = n] \]

斯特林反转

\[f(n)=\sum_{k = 0}^{n}\left\{\begin{array}{l}n\\k\end{array}\right\}g(k)\Longleftrightarrow g(n)=\sum_{k = 0}^{n}(-1)^{n - k}\left[\begin{array}{l}n\\k\end{array}\right]f(k)\\ f(m)=\sum_{k = m}^{n}\left\{\begin{array}{l}k\\m\end{array}\right\}g(k)\Longleftrightarrow g(m)=\sum_{k = m}^{n}(-1)^{k - m}\left[\begin{array}{l}k\\m\end{array}\right]f(k) \]

带入用反转公式可以验证。

总结一下：

上升下降幂的互相转换： \(n^{\overline{m}}=(n + m - 1)^{\underline{m}}\) 和 \(x^{\underline{n}}=(-1)^{n}(-x)^{\overline{n}}\)

普通幂转下降幂：\(x^n=\sum_{k = 0}^{n}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\underline{k}}\)

下降幂转普通幂（由斯特林反演得）：\(x^{\underline n} = \sum^n_{k=0}(-1)^{n-k}{n\brack k}x^k\)

上升幂转普通幂：\(x^{\overline n} = \sum^n_{k=0}{n\brack k}x^k\)

普通幂转上升幂（由斯特林反演得）：\(x^n=\sum_{k = 0}^{n}(-1)^{n-k}\left\{\begin{matrix}n\\k\end{matrix}\right\}x^{\overline{k}}\)

斯特林数与生成函数

第一类斯特林数的二元生成函数：

这里盒子无标号，数字有标号，所以是 x 的 EGF，y 的 OGF。

\[S1(x,y)=\sum\limits_{i=0}\sum\limits_{j=0}\begin{bmatrix}i\\j \end{bmatrix}\dfrac{x^iy^j}{i!}=(1-x)^{-y} \]

证明：

主要思路是先得到只有一个置换环时的的生成函数，然后用 exp 的惊天组合意义得到 y 行的生成函数。

一个环排列的 EGF 为 \(F(x)=\sum\limits_{i=0}\begin{bmatrix}i\\1 \end{bmatrix}\dfrac{x^i}{i!}=\sum\limits_{i=1}\dfrac{x^i}{i}=-\ln(1-x)\) 。

现在要把圆排列组合成置换，由于用 \(y\) 的次数来记录环的个数，因为现在之统计单个环，只有 \(y = 1\) 时有系数，所以单个环排列的生成函数变为 \(yF(x)\)。

根据 exp 的组合意义，置换的生成函数即为 \(\exp\big(yF(x)\big)=\exp\big(-y\ln(1-x)\big)=(1-x)^{-y}\)。

第一类斯特林一行的生成函数

也就是固定上指标，求下指标的生成函数。所以要取 \(n![x^n]\) ，得到的是关于盒子的 OGF：

\[\begin{aligned} &n^{-y}\\ =&n![x^n]\sum_i(-x)^{i}\binom {-y}i 广义二项式定理\\ =&n!(-1)^{n}\dfrac{(-y)^\underline n}{n!}\\ =&(-1)^{n}{(-y)^\underline n}\\ =&{y^\overline n}\\ \end{aligned} \]

这相当于证明了之前我们用数学归纳法凑出来的式子：\(x^\overline n=\sum {n\brack i}x^i\)，上升幂转普通幂。

如果要求 \(y^\overline n\) 的系数，可以使用分治 FFT \(O(n\log^2n)\)，也可以使用多项式平移 \(O(n\log n)\). 详见这里

第一类斯特林一列的生成函数

也就是盒子（置换环）数固定，小球数不定的方案数，得到的时关于球的 EGF。这里要提取 \(y^n\) 项系数，而 y 在指数上，所以可以转化成 exp 的形式

\[\begin{aligned} &[y^n](1-x)^{-y}\\ =&[y^n]\exp(yF(x))\\ =&[y^n]\sum\dfrac{y^iF^i(x)}{i!}\\ =&\dfrac{(-\ln(1-x))^n}{n!}\\ \end{aligned} \]

第二类斯特林数的二元生成函数

小球有标号，用 EGF，盒子无标号，用 OGF。

\[\begin{aligned} &S2(x,y)\\ =&\sum_i\sum_j{i\brace j}\dfrac{x^iy^j}{i!}\\ =&\exp(y(e^x-1))\\ \end{aligned} \]

推导：只有一个无标号非空盒子方案的生成函数：\(\sum_{i=1} \dfrac{x^i}{i!} = e^x-1\).

然后因为 y 是盒子数，一个盒子的时候是 \(y(e^x-1)\) ，又根据 exp 惊天组合意义，得到最终的答案：

\[\exp(y(e^x-1)) \]

补充

高阶差分与第二类斯特林数有奇妙的性质：

\[\left.\Delta^{m}x^{n}\right|_{x = 0}=m!\begin{Bmatrix}n\\m\end{Bmatrix} \]

伯努利数

我们可用有限积分求自然数下降幂的和，结果发现自然数普通幂的和我们居然还不会求？

我们定义 S：

\[S_m(n)=\sum_{i=0}^{n-1}i^m \]

可以发现这可以表示为 \(m + 1\) 次的多项式，可以拉差出它的系数，发现它的系数似乎很有规律。

假设 \(B(x) = \dfrac x{e^x - 1}\)，用 \(B_i\) 表示 \(i![x^i]B(x)\) 则有：

\[S_m(n) = \frac 1{m + 1} \sum_i^m \binom{m+1}iB_i n^{m+1-i} \]

序列 B 就是伯努利数，然后 \(B(x)\) 被称为伯努利数的 EGF。

推论：\(\sum_i^m \dbinom{m+1}iB_i =[m = 0]\).其实就是带入 \(n = 1\) 即可得到。不过没有用。

小小变化一下式子还可以得到：

\[\sum_{i = 0} ^{n-1}i^k=k!\sum_{i=0}^k\dfrac{B_{k-i}n^{i+1}}{{(k-i)!}(i+1)!} \]

给一个生成函数的证明：

为了方便使用生成函数，定义 \(F_n(x) = \sum\limits_{i}(\sum\limits_c^{n-1}c^i)\dfrac{x^i}{i!}\)，则有 \(S_m(n)=m![x^m]F_n(x) = \sum\limits_{i=0}^{n-1} i^m\)，继续推导 \(F\) 的式子：

\[\begin{aligned} F_n(x) =& \sum_{i}\sum_c^{n-1}\dfrac{c^ix^i}{i!}\\ =& \sum_c^{n-1}\sum_{i}\dfrac{(cx)^i}{i!}\\ =& \sum_c^{n-1}e^{cx}\\ =& \frac{e^{nx} - 1}{e^{x}-1}\\ \end{aligned} \]

其实如果只求自然数幂的和的话到这一步就可以了，但是为了装逼证明前面那个式子的正确性，还可以继续推导：

令 \(B(x) = \dfrac x{e^x-1},G(x)=\dfrac {e^{nx}-1}x\)，则 \(F_n(x)=B(x)G(x)\).

\[\begin{aligned} G(x) &=\dfrac {e^{nx}-1}x\\ &= \frac 1x\sum_{i=1}\frac{n^ix^i}{i!}\\ &= \sum_{i=0}\frac{n^{i+1}x^i}{(i+1)!}\\ \end{aligned} \]

所以有：

\[\sum_{i = 0} ^{n-1}i^k=k![x^k]B(x)G(x)=k!\sum_{i=0}^k\dfrac{B[k-i]n^{i+1}}{(i+1)!} \]

这里的 \(B[k-i]\) 表示 \(x^{k-i}B(x)\).

这玩意最大的用处就是 k 很小 n 很大的时候可以把求和上界从 n 变成 k，还有一个用是把枚举上界从 n - 1 改为 k + 1，方便推式子。不过话说这玩意如果只求一个数的话可以直接拉差，如果要求多个数的话可以多项式多点求值。综上所述，学这玩意大概率八辈子都用不到。

总结：自然数 k 次方和问题 \(f_k(n)=\sum_{i=0}^{n-1}i^k\)

当 k 足够小（比如 1，2，3，4 这种小常数）的时候，可以暴力把普通幂拆成下降幂，然后用有限积分做。例如 \(x^2=x^\underline 2 + x^\underline 1\).

如果 k 不能当成常数，但是 n 远大于 k 时，那么可以推一下式子得到 \(f_k(n)=\sum_{j=0}^k\dfrac{k\brace j}{j+1}n^\underline{j+1}\)，可以花 \(O(k\log k)\) 的时间预处理出一行的斯特林数，然后 \(O(k)\) 地得到一个 \(f_k(n)\)，聪明一点的会发现上式可以当成 n 的 k + 1 次多项式，可以拉差出 f 的第 n 项。还更快。

如果需要求出多个甚至每一个 k 时的答案，可以考虑用伯努利数，或者直接莽一个多项式多点求值，不过前者是但 log，后者是双 log

小推一下式子可以得到 f 在 k 上的 EGF 是 \(\dfrac{e^{nx} - 1}{e^{x}-1}\)，取 \(k![x^k]\) 即可得到答案。

如果 k 固定，对不同的 n 求这个东西，那么显然有 \(f_k(n)=f_k(n-1)+(n-1)^k\)，如果 n 连续并且从 0 开始，直接递推就可以了，如果 n 连续但是不从 0 开始，可以先拉差出第一项。如果 n 不连续应该可以多项式多点求值，不过我没试过，理论可行。

欧拉数

这个更是没用

定义 \(\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle\) 为有 \(k\) 个升高的，长度为 \(n\) 的排列的个数。其中“升高”定义为让 \(p_i<p_{i+1}\) 成立的 \((p_i,p_{i+1})\)。

递推式：

\[\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle=(k+1)\left\langle\begin{matrix}n-1\\k\end{matrix}\right\rangle+(n-k)\left\langle\begin{matrix}n-1\\k-1\end{matrix}\right\rangle \]

解释：不妨从小到大地插入数字。考虑最后插入的数，如果插到一个升高的中间，原本的升高没了，但是又多一个升高，总个数还是不变 \(k\left\langle\begin{matrix}n-1\\k\end{matrix}\right\rangle\)。如果插入到最开始的位置，升高肯定不变 \(\left\langle\begin{matrix}n-1\\k\end{matrix}\right\rangle\)。因为最后插入的数字最大，所以插入到其他地方一定升高加 1 \((n-k)\left\langle\begin{matrix}n-1\\k-1\end{matrix}\right\rangle\)。加起来就是原式。

推导欧拉数·行的生成函数

这里有个模板题：P5825 排列计数 - 洛谷。

设 \(g(k)\) 表示长度为 n 的排列恰好 k 个升高的方案数，也就是答案 \(\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle\) ，\(f(k)\) 表示长度为 n 钦定 \(k\) 个升高的方案数，容易得到：

\[g(k) = \sum_{i=k}^n(-1)^{i-k}\binom ikf(i) \]

考虑这么搞 f。

我们把连续的上升叫做一个 "段"，现在相当于求钦定了 \(n-i\) 个段的方案数。

先考虑只有一个段，个数到方案的函数是 \(P(n)= [n\neq 0]\).思考该用 OGF 还是 EGF。

如果有两个段，那么方案数 \(P'(n)=\sum \dbinom niP(i)P(n-i)\)，这里要乘上一个分配数的方案 \(\dbinom ni\) ，所以其组合意义是 EGF。

容易得到 P 的 EGF 是 \(e^x-1\)，那么 k 个段的 EGF 就是 \((e^x-1)^k\)，然后再取 n 次项系数得到：

\[f(n-k)=n^k \]

（注意：欧拉数没有要求内部是连续的，所以有一个选数的过程，肯定会乘上一个归并的系数，要用 EGF，而之前的 queue2 要求内部连续，这里 的组合意义是有序拼接，所以只用在最后乘上一个外部排列方案数，用 OGF。）

然后带入 g 得到：

\[\begin{aligned} g(k) &= \sum_{i=k}^n(-1)^{i-k}\binom ikn^{n-i}\\ &= \sum_{i=k}^n(-1)^{i-k}\binom ikn![x^n]\sum_j^{n-i}\binom {n-i}je^{jx}(-1)^{n-i-j}\\ &= \sum_{i=k}^n(-1)^{i-k}\binom ik\sum_j^{n-i}\binom {n-i}jj^{n}(-1)^{n-i-j}\\ &= \sum_j^{n-k}(-1)^{n-k-j}j^{n}\sum_{i=max(k,j)}^n\binom ik\binom {n-i}j\\ &= \sum_j^{n-k}(-1)^{n-k-j}j^{n}\binom {n+1}{k+j+1}\\ \end{aligned} \]

最后一步范德蒙德卷积的范围可以仔细推一下，可以发现在后面表达式在 \(i< max(k,j)\) 时，值都是零。

把组合数拆了，然后设 \(f(j)=j^n,g(k+j)=(-1)^{n-k-j}\dbinom {n+1}{k+j+1}\)，然后做差卷积就行了。

欧拉数还满足如下恒等式 :

\[x^n=\sum\limits_{k=0}^n\left\langle\begin{matrix}n\\k\end{matrix}\right\rangle\dbinom{x+k}{n} \]

欧拉数的二元生成函数为 ：

\[E(x,y)=\sum\limits_{n=0}\sum\limits_{m=0}\left\langle\begin{matrix}n \\ m\end{matrix}\right\rangle\dfrac{x^ny^m}{n!}=\dfrac{1-y}{e^{x(y-1)}-y} \]

分拆数

模板题链接

定义：记 \(P_n\) 为将 n 拆分成若干个若干无序正整数的和的方案数。

如 \(3\) 可以拆分成 \(1+1+1\) 或 \(1+2\) （和 \(2+1\) 视为同种方案）或 \(3\)。于是 \(P_3=3\)。

可以发现，分拆数本质上是所有种类的质量的物品都有的完全背包方案数，于是按照背包套路能写出它的 OGF:

\[P(x)=\prod_{k = 1} \sum_{i = 0}x^{ik} = \prod_{k=1}\frac{1}{1-x^k} \]

然后 ln，exp：

\[\exp(\sum_{k=1}\ln\frac{1}{1-x^k}) = \exp \sum_{k=1}\sum_{i=1}\frac {x^{ki}}i \]

发现后面暴力求解的复杂度是调和级数，再套一个 exp 板子即可。

五边形数定理

用处1. 在没有 ntt 模数时，而且你有懒得写 mtt 时，但是你要求分拆数时，并且时间有比较充裕够根号的复杂度时，而且时间又不太充裕不能暴力时用。

用处2. 在每个数的使用次数有统一上界时用。例如上界为 k 时有 ： $$P(x)=\prod_{k=1}\sum_{i=0}^{K-1}x=\prod_{k=1}\dfrac{1-x^{kK}}{1-xk}$$。

对于刚才式子分母的展开后发现：

\[\prod_{i=1} (1-x^i) = 1-x-x^2+x^5+x^7-x^{12}-x^{15}+\cdots \]

然后合理猜测发现：

\[\prod_{i=1}(1-x^i)=1 + \sum_{i=1}(-1)^ix^{i(3i\pm 1)/2} \]

证明过于鬼畜，我不会。然后上面的等式叫做五边形数定理，名字来于 x 的次数为五边形套娃后合法点数构成的递推式拓展到整数后的数列。、

Ferrers 图（又称杨表）

在分拆数的基础上，要求拆分出来的数不超过 m 个。

有一个非常人类智慧的做法，就是对于每个正确的方案，用柱状图来表示，例如：

拆分 \(1+1+2+4+5\) 的 Ferrers 图如下所示 ：

\[\begin{aligned} &5 : \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &4 : \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &2 : \blacksquare\ \blacksquare\\ &1 : \blacksquare\\ &1 : \blacksquare\\ \end{aligned} \]

然后竖着看这个图（也就是把原来的一列当成一排）：

\[\begin{aligned} & 5\ \ 3\ \ \ 2 \ \ 2\ \ 1 \\ &\blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &\blacksquare\ \blacksquare\ \blacksquare\ \blacksquare\\ &\blacksquare\ \blacksquare\\ &\blacksquare\\ &\blacksquare\\ \end{aligned} \]

然后非常神奇的事情发生了！你发现惊奇地问题变成统计每个数都小于 m，但是不限制拆分的数的个数时的方案数！而且仔细想一下发现这甚至是意义对应的的！然后就可以快乐地转化问题了。

这只是做一个改了一下上界的分拆数，外重循环的上界是 m ，即：\(\exp \sum_{k=1}^m\sum_{i=1}\frac {x^{ki}}i\) 复杂度显然还是 \(O(n\log n)\).

神秘结论：对于 \(n\) 的分拆， 各个分拆方案中出现至少 \(k\) 次的数的个数和，等于所有方案中 \(k\) 出现的总次数。证不来，根本证不来！