多项式全家桶【长期更新】
多项式
做多项式题就像嗑药,出多项式题就像贩毒。—— 某 FJ 知名 OI 选手
定义(表达式)
定义一个 \(n\) 次的多项式为:
注意 :
- \(i=0\) 的那一项是常数项。
- 易得\(F(0) = f_0\)
- 在OI中,多项式一般在同余条件下讨论\((mod\ p)\),在下文中会省略 "$\huge\equiv $" 符号。
- 求多项式\(F(x)\),实际上就是把每一个\(f_i\)求出来。
暴力全家桶
加法
给定两个多项式 $ F(x) $ 和 $G(x) $,求它们的和 $ H(x) $。
即: $ H(x) = F(x) + G(x) \(
\) h_i = f_i + g_i $
(类比高精度加法)
复杂度 $ O(n) $
乘法
即:\(H(x) = F(x)G(x)\)
就是合并同类项
复杂度 \(O(n^2)\)
余数除法
已知F和H,求G和R
即:\(H(x) = F(x)G(x) + R(x)\)
就是小学奥数里的大除法。
\(O(n^2)\)
求导和积分
若:\(G(x) = F'(x)\)
则:\(g_i = (i+1)\times f_{i+1}\)
若:\(H(x) = \int F(x)dx\)
则:\(h_i = \frac{f_{i-1}}{i}\)
求逆
F 已知求 G。
即:\(F(x)G(x) = 1(mod\ p)\)
递推求即可。
\(O(n^2)\)
开根
\(G^2(x) = F(x)\),已知F求G
还是用递推,\(O(n^2)\)
特别的,\(g_0^2 = f_0\) 作为边界情况。
-
若 \(f_0\neq0\),则 \(G\) 的解数,取决于 \(f_0\) 的平方根数量。(具体参见二次剩余)
-
若 \(f_0=0\),令 \(F(x)=x^kH(x)\),满足 \(h(0)\neq0\),那么若 \(k\) 为奇数,则 \(G\) 无解;若 \(k\) 为偶数,记 \(P^2(x)=H(x)\),那么 \(G(x)=x^{\frac k2}P(x)\)。
这是因为开跟运算本身不一定有解。
求对数
给定多项式 $ F(x) $,求 $ G(x) \equiv \ln F(x) \pmod{x^n} $,保证 $ f_0 = 1 $。
解:对原等式两边求导,得:
\(O(n^2)\)
求指数
给定多项式 $ F(x) $,求 $ G(x) \equiv e^{F(x)} \pmod{x^n} $,保证 $ f_0 = 0 $。
对原等式两边求导,得:
$ g_0 = e^{f_0} = e^0 = 1 $
此式子也可看成求对数的第三步和第四步,把F换成G,把G换成F
求 $ g_{i+1} $ 时已求出 $ g_0 $ 到 $ g_i $, 故可以递推求出 $ G(x) $
\(O(n^2)\)
求三角函数
前置知识:[欧拉公式(\(e^{ix}的代换\))](https://www.cnblogs.com/water-flower/p/18651768#- 定义五:在复数中的定义(欧拉公式)-) ,泰勒展开
由欧拉公式:
两式相加得
两式相减得
现在我们把三角函数换成了指数函数,用指数的方法来推导三角函数。
\(O(n^2)\)
快速傅里叶变换
终于进入正题了。
前置内容
-
多项式插值:n + 1 个点值可确定一个 n 次多项式。
很好理解。用待定系数法高斯消元。
系数矩阵满秩,所以不会是无数解。
有如果无解,说明有两行的系数,上面的系数都是下面的系数的k倍。但是对于不同的x,\(\{x^i\}\) 的集合不会是这种比例关系。
-
复数运算:参见数学书
-
单位根
P.S. 以下为了方便书写,均将 \(\omega\) 简写为 \(w\),且将 \(\omega_n^i\) 表示为 \(w_i\)。定理:任何复系数一元n次多项式方程在复数域上至少有一个根。
大多数数学家都认为这是对的。
推论:任何复系数一元 \(n\) 次多项式方程在复数域上恰好有 \(n\) 个根。
设现有一根 \(x_i\)。
若将原 n 次多项式因式分解,必定存在一项形如 \((x - x_i)\)。把这一项去掉,得到一个 n-1 次的多项式。而这个新的多项式必有一根。再把这个根去掉。重复这个操作。因为可以降幂 n 次,所以有 n 个根。
单位根定义:\(x^n−1=0\) 的 \(n\) 个根,记作 \(w_0,w_1...w_{n-1}\)。
单位根几何意义:建立复数域的坐标系。做单位圆。运算用向量的运算。这里以 \(n=6\) 为例。
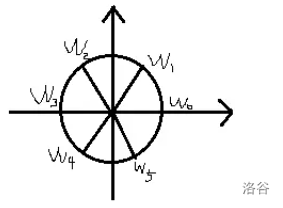
用三角函数来表达这些单位根可得: \(w_i = \cos{2i\pi\over n} + i\sin{2i\pi\over n}\)
首先显然有:\(w_{kn+i} = w_i\),这相当与多转 k 圈。
通过化简,\((w_i)^2 = (\cos{2i\pi\over n} + i\sin{2i\pi\over n})^2= \cos2{2i\pi\over n} + i\sin2{2i\pi\over n} = w_{2i}\),这个可以看为把和x轴的夹角翻倍。
同理(大概是用一些二项式定理和欧拉定理展开后乱搞),\((w_i)^n = w_{in} = w_0\)
所以一个单位根的 \(n\) 次方都是 \(1 + 0i\)
下面给出一些关于单位根的运算性质 :
-
\(w_{i+n}=w_i\)
-
\(w_iw_j=w_{i+j}\)
-
\((w_{i})^j=w_{ij}\) 次方转下标
-
\(-w_i=w_{-i}\)
-
\(w^{ki}_{kn} = w^{i}_{n}\)
单位根反演
(应该只在 IDFT 的证明中有用到)
这里用 \(w_i\) 代表 \(w_i^n\)
\[\sum\limits_{i=0}^{n-1}{w_i^k}=n[n\mid k] \]证明:
\[\sum\limits_{i=0}^{n-1}{w_i^k} = \sum\limits_{i=0}^{n-1}{w_k^i} \]该式为等比数列,所以:
\[\sum\limits_{i=0}^{n-1}{w_k^i} = \begin{cases} &n \text{ if } w_k = 1 \\ &{1 - w_k^n \over 1 - w_k} \text{ if } w_k != 1 \end{cases} \]观察到,\(w_k^n = w_{nk} = 1\),并且 \(w_k = 1 \Leftrightarrow n|k\)
所以上式化简为:\(\sum\limits_{i=0}^{n-1}{w_i^k}=n[n\mid k]\)
-
FFT
这玩意可以做到 \(O(n\log n)\) 的多项式乘法。老牛逼了。
核心思路
根据多项式插值,我们根据 \(F(x)G(x)\) 的 n + 1 个点值,然后用插值法,可以插出这个多项式。
通过优秀的选点(单位根),可以做到 \(O(n\log n)\)。
现在我们有两个要做的事情:
- DFT:输入一个 \(n-1\) 次多项式的系数列,快速得到其在 \(n\) 次单位根处的点值列,也就是求 \(F(w_i)\)。
- IDFT:在优秀的时间复杂度内插值出多项式,也就是用 \(H(x_i)\) 去求 \(h_i\)(点值求系数)。
具体做法
先来解决DFT:
带入 \(w_k(k < {n \over 2})\),\(F(w_k) = F1(w_k) + w_kF2(w_k)\)
带入 \(w_{k + {n\over 2}}(k<{n\over 2})\),\(F(w_k) = \sum\limits^{\frac n2-1}_{i=0}f_{2i}w_{k}^{2i} + w_{k+{n\over 2}}^1\sum\limits^{\frac n2-1}_{i=0}f_{2i+1}w_k^{2i}\)
\(w_{k + {n\over 2}}^{2i} = w_{2k + n}^{i} = w_{2k}^{i} = w_{k}^{2i}\),\(w_{k+{n\over 2}} = w'_{k}\) 这里 \(w_{k+{n\over 2}}\) 以 \({n\over 2}\) 为底, \(w'_k\) 以 n 为底。
所以带入 \(w_{k + {n\over 2}}(k<{n\over 2})\),\(F(w_{k+\frac n2}) = F1(w_k) - w_kF2(w_k)\)
于是可以递归求解。
复杂度是 \(T(n)=2T(\frac n2)+O(n)\) ,是 \(O(n\log n)\) 的
可以发现,DFT能做到高效的原理实际上是利用的单位根的运算性质。
再来看IDTF:
根据单位根反演可以推到出这个公式:
证明:
这个公式与DTF相比,左边多一个 n ,右边的 k 变成了 -k,其余一致。
常数优化:非递归FFT
注意到,第 k 个点和第 k + len / 2 个点 由 第 k 个点和第 k + len/2 共同转移来,并且每次len除2。
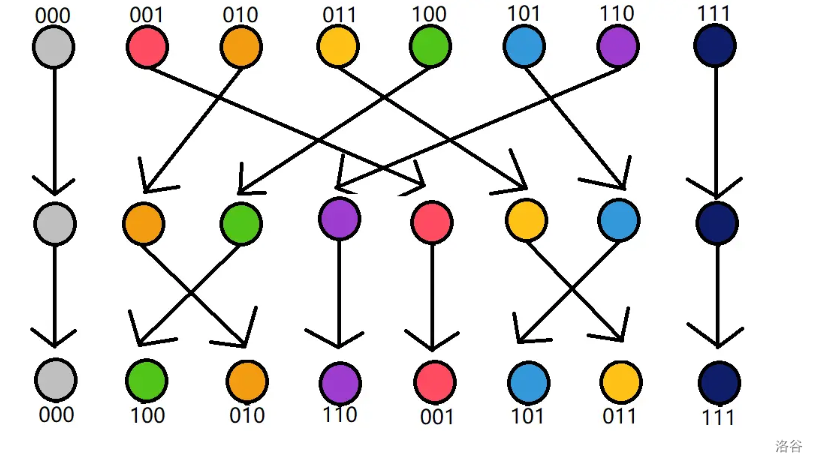
若执行到了第 k 次,那么把从右往左数第 k 位是 0 的数往前提。
所以对于最后一排,最后一位是 0 的排在前面,如果最后一位都是 0,那么倒数第二排是 0 的排在前面...以此类推。
容易发现,这相当于倒着比较二进制数的大小。
考虑最后一行的初始化:第 i 位就应该为 \(f_ {\sim i}\),$\sim $表示二进制取反。
写成代码是这样的:
for (int i = 0; i < len; ++i) {
rev[i] = rev[i >> 1] >> 1;
if (i & 1) rev[i] |= len >> 1;\\变换最高位从左往右第一位?神秘
}
for (int i = 0; i < len; ++i) if (i < rev[i]) swap(y[i], y[rev[i]]); \\这样才能刚好交换一次
之后就可以从低位向高位递推了。
附上代码:
typedef complex<double > com;
const int N=(1e6+6) * 4;
const double PI = acos(-1);
int n,m,rev[N];
com f[N],g[N];
void change(int n) {
int L = log2(n);
for(int i=0;i<n;++i)rev[i] = (rev[i>>1]>>1) | ((i&1) << (L-1));
}
void FFT(com *f, int n,int op) {
change(n)
for(int i=0;i<n;++i) if(rev[i] < i) swap(f[i], f[rev[i] ]);
for(int mid = 1;mid < n;mid <<= 1){
int j = mid << 1;
com nxt(cos(PI / mid), sin(PI / mid) * op);
for(int st = 0;st < n; st += j){
com w(1.0, 0.0);
for(int i = st;i < st + (j>>1); ++i, w *= nxt){
com tmp1 = f[i],tmp2 = w * f[i + mid];
f[i] = tmp1 + tmp2;
f[i + mid] = tmp1 - tmp2;
}
}
}
}
NTT
除法意味着精度误差,所以很多人不喜欢除法,而使用在模数的逆元来替代除法。
FFT用的是单位根的点值,而NTT则运用原根,并且可以避免除法运算,被广泛使用。
原根定义:对于模数 \(m\),满足 \(\gcd(g,m)=1\) 且 \(g^k\equiv 1(\bmod m)\) 最小正整数 \(k\) 等于 $\varphi(m) $ 的一个数 \(g\)。注意,一个模数 \(m\) 可能有多个原根。
原根有和单位根一样优良的性质。设 \(g\) 表示 \(p\) 的一个原根,则令 \(w_i=g^{i\frac{\varphi(p)}n}\) :
- \(w_{i+n}=w_i\)
- \(w_iw_j=w_{i+j}\)
- \(w_{i}^j=w_{ij}\)
- \(\frac 1{g_i}=g_{-i}\)
- \(g^{i\frac{\varphi(p)}n}\) = \((g^{\frac{\varphi(p)}n})^i\)
但是这不代表我们可以直接将他套用进 FFT 中。因为这里必须要求 \(n\mid \varphi(p)\),所以这对 \(n\) 产生了很大的限制。
幸运的是我们发现质数 \(998244353\) 的欧拉函数值 \(998244352=119\times2^{23}\),因此当 \(n\leq 2^{23}\) 时,都能够很好的进行这个算法,\(2^{23}\) 比 \(O(n\log n)\) 算法能通过的数据范围略大一点,所以大多数时候可以直接使用这个NTT算法,这也是 \(998244353\) 成为常用模数的原因。(尽管有些时候题目与多项式无关)
\(998244353\) 的原根有\(3\) 和 \(114514\)。这使得这个数字充满了美好的寓意
代码(摘自 oi-wiki.org)
void ntt(int *x, int lim, int opt) {
int i, j, k, m, gn, g, tmp;
for (i = 0; i < lim; ++i)
if (r[i] < i) swap(x[i], x[r[i]]);
for (m = 2; m <= lim; m <<= 1) {
k = m >> 1;
gn = qpow(3, (P - 1) / m);
for (i = 0; i < lim; i += m) {
g = 1;
for (j = 0; j < k; ++j, g = 1ll * g * gn % P) {
tmp = 1ll * x[i + j + k] * g % P;
x[i + j + k] = (x[i + j] - tmp + P) % P;
x[i + j] = (x[i + j] + tmp) % P;
}
}
}
if (opt == -1) {
reverse(x + 1, x + lim);
int inv = qpow(lim, P - 2);
for (i = 0; i < lim; ++i) x[i] = 1ll * x[i] * inv % P;
}
}
快速多项式全家桶
加法和乘法和求导积分略过。
前置知识:牛顿迭代
对于一个方程 \(F(x) = 0\) 求近似解,我们先瞎猜一个解 \(x\) ,算出 \(F(x)\) 在 \((x, F(x))\) 处的切线,算切线与 \(x\) 轴的交点,把交点 \(x_1\) 当成新的解并重复此操作。
当我们把 \(x\) 换成一个函数,我们发现牛顿迭代又可以用于求解函数。
假如一个函数 \(F(x)\) 满足一个关系 \(G(F(x))=0\),这里会把 \(F(x)\) 当作未知量,并且 \(G\) 是一个泛函数。
为了方便表示,设 \(F_k \equiv F(\bmod x^{2^k})\) ,能得到 \(F_k\) 满足 \(G(F_k) \% x^{2^k} = 0\),我们希望用 \(F_k\) 求出 \(F_{k+1}\),直到达到精度要求。
那么如果我们先预估一个函数 \(F_0(x)\),就能得到 \(F_1(x)=F_0(x)-\frac{G(F_0(x)))}{G'(F_0(x))}\) ,并不断继续重复以提高精度。
证明:
因为 \(G(F_{k+1}(x))\%x^{2^{k+1}}=0\),将其在 \(F_k\) 处泰勒展开得:
为了求 \(F_{k+1}\) 我们将其对 \(x^{2^{k+1}}\) 次方取模
因为 \(F_k\) 是 \(2^k\) 次的,所以 \((F_{k+1}(x)-F_k(x))^i\) 的最低次项是 \(2^{ki}\) 次的,所以只有 \(i\) 等于 \(0,1\) 时才有值。化简上式:
求逆
F已知求G。
即:\(F(x)G(x) = 1(mod\ p)\)
我们要想办法把这玩意化成可以牛顿迭代的形式:
可以得到 \(H(G) = {1\over G} - F = 0\)。因为 F 已知,这里被当作常数,所以 H 就是关于 G 的函数。
迭代的初值 : \(g_0 = f_0^{-1}\) (带入 \(x = 0,f_0^{-1}\) 用普通的求逆元的方法即可)
使用牛顿迭代的公式得到 : \(G_{k+1} = G_k - {H(G_k)\over H'(G_k)} = \large{G_k - {{1 \over G_k } - F\over-{1\over G_k^2}}}\)
我们对这个式子化简(分子分母同乘 $G_k^2 $ )可得: \(G_{k+1} = 2G_k - FG_k^2\).
时间复杂度 \(T(n) = T(n/2) + O(n\log n) = O(n\log n)\).
余数除法
已知F和H,求G和R
即:\(H(x) = F(x)G(x) + R(x)\)
思路:如果没有 R(x),这个题就用逆元做,所以要想办法避开 R.
用普通的方法很难求,但是观察到,R 的次数比 H 低,于是考虑把函数系数翻转后,发现R的后几项的系数为0,再用取模的方式把 R 干掉。
做法:设 \(n=\deg H,m=\deg F\)
设 \(rH(x)=x^nH(\frac 1x)\),即把 \(H(x)\) 系数翻转之后得到的函数,同理有 \(rF(x)=x^mF(\frac1x)\) 和 \(rG(x)=x^{n-m}G(\frac1x)\) 和 \(rR(x)=x^{m}R(\frac1x)\)。
容易得知 \(rF(x)\equiv rQ(x)rG(x)\pmod{x^{n-m+1}}\)
证明:
\(rG\) 的次数刚好是 \(n-m\) 次的,所以可以用求逆的方法算出 \(rG\) ,于是可以算出 \(G\),于是可以算出 \(R\)
复杂度同求逆 \(O(n\log n)\).
开根
\(G^2(x) = F(x)\),已知F求G
转成可以牛顿迭代的形式:\(H(G) = G^2-F = 0\).
\(O(n\log n)\)。
特别的,\(g_0^2 = f_0\) 作为边界情况。
-
若 \(f_0\neq0\),则 \(G\) 的解数,取决于 \(f_0\) 的平方根数量。(具体参见二次剩余)
-
若 \(f_0=0\),令 \(F(x)=x^kH(x)\),满足 \(h(0)\neq0\),那么若 \(k\) 为奇数,则 \(G\) 无解;若 \(k\) 为偶数,记 \(P^2(x)=H(x)\),那么 \(G(x)=x^{\frac k2}P(x)\)。
这是因为开跟运算本身不一定有解。
ln
给定多项式 $ F(x) $,求 $ G(x) \equiv \ln F(x) \pmod{x^n} $,保证 $ f_0 = 1 $。
解:对原等式两边求导,得:
\(g_0 = 0\)
\(O(n\log n)\)
exp
给定多项式 $ F(x) $,求 $ G(x) \equiv e^{F(x)} \pmod{x^n} $,保证 $ f_0 = 0 $。
$ g_0 = e^{f_0} = e^0 = 1 $
对两边取 \(\ln\) :
\(O(n\log n)\)
求三角函数
\(i = w^1_4=g^{(p-1)/4}\) 当 \(g = 998244353\),\(i\equiv86583718\)。
现在我们把三角函数换成了指数函数,用指数的方法来推导三角函数。
\(O(n\log n)\)
快速幂
直接快速幂是两个 log。由于多项式支持 exp 和 ln,于是 \(F^k(x) = e^{k\ln F(x)}\)。这样就是一个 log 了。
如果 k 很大,可以让 k 对 mod 取模,因为变化过的式子 k 只是 F(x) 的一个系数罢了。
多项式与分治
给定长为 \(n\) 的序列 \(a_i\),求多项式 \(\prod_{i=1}^n(x-a_i)\)。
\(n\leq10^5\)。
看作两个多项式相乘,用 FFT
\(T(n) = 2T(n/2) + O(n\log n)=O(n\log^2 n)\)
多项式平移
已知 \(F(x)\) 的系数,求 \(F(x+c)\) 的系数。
记 \(f_i=[x^i]F(x)\),则有:
二项式展开得:
令 \(i!f_i = [x^i]A(x),\dfrac {c^i}{i!}=[x^i]B(x)\),则上式改写为:
为了得到卷积的形式,把 \(A\) 的系数反转得到 \(A'\):
用 \(NTT\) 优化即可。
常系数齐次线性递推
求一个满足 \(k\) 阶齐次线性递推数列 \({a_i}\) 的第 \(n\) 项,即:
这里先讲多项式取模的做法。
以斐不拉契为例,\(F_3 = F_2 + F_1 = (F_1 + F_0) + F_1\)。这是一个不断把最高位的项用递推表达式替换成之后的项的过程。
考虑如何刻画这个过程。
我们直接用 \(x^n\) 对多项式 \(P(x) = x^k - \sum \limits_{i=1}^{k} f_ix^{k-i}\) 取模,发现这和上述过程等价。就没了。
还有另一个做法。
设 \(F(x)\over G(x)\)\(=A(x)\) 。A 是序列 a 的 OGF。
现在变成了一个构造题。你要构造一个合法的 F 和 G。
不妨让 F 大于等于 k 的项都为 0。
又因为
不妨让 \(G_0 = 1,G_{[1,k]} = -f_{[1,k]},G_{[k+1,n]} = F_{[k,n]} = 0,F\equiv GA\bmod x^k\)。这就是一组合法的 FG。
如果想要更深入的理解第二种做法,强烈建议用你原来的方法手算斐不那契数列表达式,然后对比用这个公式算出来的答案,再反过来思考这个方法的正确性,然后你就能很彻底的理解这个公式了!(本质上就是凑)
最后用 Bostan-Mori 求 A 的第 n 项,如果 G 刚好可以因式分解,就可以使用有理展开定理。这个做法常数略小一点。
两个做法的复杂度都是 \(O(k\log k)\)
参考资料:上课的课件,大佬的博客。
冷知识:多项式对数是洛谷原创。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号