向量基础

向量基础

定义

物理定义：有方向有长度的线段。

信息学表示法：以这个向量的出发点为坐标原点，这个向量的终点坐标。一般写作竖着的一列数。

模长：向量的长度。

零向量：模长为 0 的向量；

单位向量：模长为 1 的向量。

例如二位向量

\[\begin{bmatrix} 3\\2 \end{bmatrix} \]

表示从原点向右走3，向上走2的点。

该向量的模长为 \(\sqrt 13\)

向量加法

就是用平行四边形法则，或者用两个向量首尾相接。

相信大家《力的合成》这一章节学的不错，这里不再赘述。

线性空间的基

平时我们用的平面直角坐标系的横轴上的点（1，0）作为 $\hat{i} $，相应的纵坐标上的点（0，1）作为 $\hat{j} $。

一个二维向量可以被表示为a被的\(\hat{i}\)，加上b倍的 $\hat{j} $。

然而我们不一定非要用\(\hat{i}\) 和 \(\hat{j}\)来表示一个向量。

对于一个二维向量，我们可以用该平面中任意两个线性无关的向量来表示这个向量。

如现在要用\(\begin{bmatrix}-1\\1\end{bmatrix}和\begin{bmatrix}1\\1\end{bmatrix}表示\begin{bmatrix}0\\1\end{bmatrix}\)

则：

\[\begin{bmatrix}0\\1\end{bmatrix} = \frac{1}{2}\begin{bmatrix}-1\\1\end{bmatrix} + \frac{1}{2}\begin{bmatrix}1\\1\end{bmatrix} \]

注意这里是向量加法。

所以\(\begin{bmatrix}0\\1\end{bmatrix}\)在用\(\begin{bmatrix}-1\\1\end{bmatrix}和\begin{bmatrix}1\\1\end{bmatrix}\)张成的线性空间中表示为\(\begin{bmatrix}\frac{1}{2}\\\frac{1}{2}\end{bmatrix}\)

矩阵/线性变换

现在想知道：

用 \(\begin{bmatrix}-1\\1\end{bmatrix}和\begin{bmatrix}1\\1\end{bmatrix}\)张成的线性空间中的向量\(\begin{bmatrix}\frac{1}{2}\\\frac{1}{2}\end{bmatrix}\)

在普通的空间（用\(\hat{i}\)和$\hat{j} $的线性空间 ）中的向量是什么。

方法如下：

1. 用两个基直接拼成一个矩阵（就是把中间两个碍事的中括号去掉）。在上面的例子中，该矩阵为：\(\begin{bmatrix}-1&1 \\1&1\end{bmatrix}\)。（注意，这里将对应\(\hat{i}\)的基放在左边，对应\(\hat{j}\)的基放在右边）
2. 用这个矩阵乘上这个向量，就是：\(\begin{bmatrix}-1&1 \\1&1\end{bmatrix} \begin{bmatrix}\frac{1}{2}\\\frac{1}{2}\end{bmatrix}\)。注意矩阵没有交换律，所以顺序不能改。

就行了。

如果要从普通的线性空间中的向量变到特定的空间中，就乘上该空间的两个基拼成的矩阵的逆。就行了。（可以用高斯消元来求矩阵的逆）

由上面的示例可以看出，矩阵可以被当成一种线性变换，其几何意义就是更换线性基后表示某个向量。

行列式（转载自JPGOJCZX的博客）

我们讲到，在线性变换中，向量的模长与方向都发生了变化，那么平面上的所有正方形的面积都发生了变化，如果把正方形的大小变得无限接近于 0，那么平面上任何一个图形都可以看做由这些小正方形组成，因此它们面积的变化都一样，而行列式正是用来刻画面积变换的一个函数。

记一次线性变换的面积变化为 \(| \det(A) |\)，其中 \(\det(A)\) 的正负由平面是否翻转决定（可以感性理解一下），它的计算式为 \(\det(A) = \displaystyle\sum_{\pi}(-1)^{r(\pi)}\displaystyle\prod_{i=1}^n M_{i, \pi_i}\)，其中 \(\pi\) 表示任意一个 \(1\) 到 \(n\) 的排列，而 \(r(\pi)\) 则是 \(\pi\) 的逆序对数量。

其实对于二维空间，n 的排列只有 {1,2} 和 {2,1} 两种，那么行列式的计算可以简化成\(\det(\begin{bmatrix} a & b \\ c & d\end{bmatrix}) = ad - bc\)，

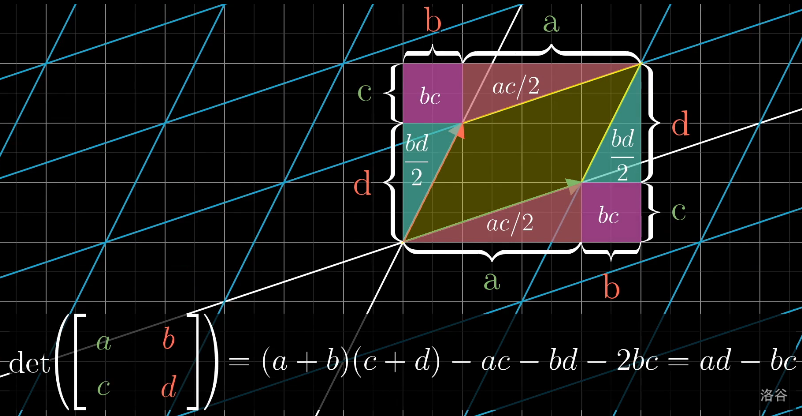
来理解。接着你会发现中小学的新定义运算中的一类经典题其实就是在求二维矩阵的行列式，原来我小学就会线性代数了啊。

当 det(M)=0 时，也就是说这个变换使得小正方形的面积变为了 0（比如映射到了同一条直线上），此时这个变换一定使空间的某一维发生了坍缩。反过来，若一个变换使得空间的某一维发生了坍缩，那么这个变换的行列式一定为 0。

向量乘法

普通乘法 （好像在多项式里有应用）

写法：把两个向量放在一起，中间没有符号。如：\(\vec{a}\vec{b}\)、\(\begin{bmatrix}-1\\1\end{bmatrix}\begin{bmatrix}1\\1\end{bmatrix}\)。

该乘积也是一个向量，其模长为两个向量模长的积，于x轴的夹角为两个向量与x轴的夹角相加。如图：

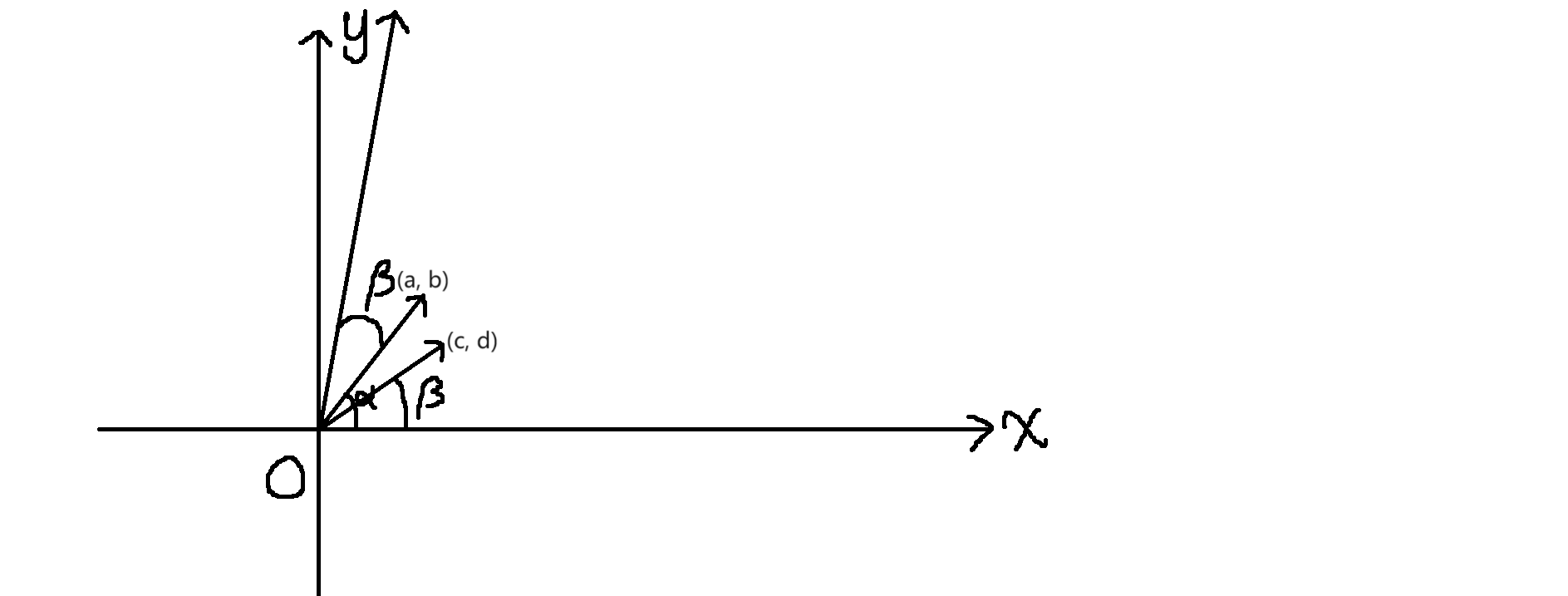
\[\left | \vec{a} \vec{b} \right | = \left | \vec{a} \right | \times \left | \vec{b} \right | \]

点积（内积）

两个向量 a=(a1,a2,…,an) 和 b=(b1,b2,…,bn) 的点积定义为：

a⋅b=a1b1+a2b2+⋯+anbn

点积的结果是一个标量（即一个数）。点积的几何意义是，它等于两个向量的模长乘以它们之间夹角的余弦值：

a⋅b=∥a∥∥b∥cosθ

其中 ∥a∥ 和 ∥b∥ 分别是向量 a 和 b 的模长，θ 是它们之间的夹角。

点积还有一个几何意义：两个向量的点积，等于一个向量 w 在另一个向量 v 上的投影的长度与 v 的模长的乘积。如图

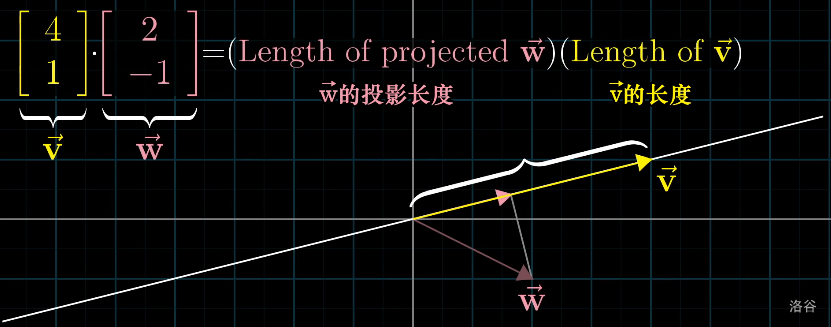
叉积（外积）

二维向量的叉积：

u 和 v 的叉积 u×v 为以 u 和 v 作为临边的平行四边形的面积，叉积的值可以通过行列式求出。

可以发现，由于行列式可正可负，因此叉积的值也可正可负，这取决于平面是否翻转。如果 u 与 v 进行叉积，则 u×v 为正，v×u 为负。

注意！二维向量叉积是一个标量，值是以 u 和 v 作为临边的平行四边形的面积

三维向量的叉积：

两个三维向量 \(a=(a_1,a_2,a_3)\) 和 \(b=(b_1,b_2,b_3)\) 的叉积定义为：

a×b=\((a_2b_3−a_3b_2,a_3b_1−a_1b_3,a_1b_2−a_2b_1)\)

事实上，狭义的叉积只对三维空间有用。当两个三维空间中的向量 u 和 v 做叉积时，可以得到另一个向量 w，满足这个向量的模长为以 u 和 v 作为临边的平行四边形的面积，垂直于这个平行四边形，且满足右手定则（三维叉乘的几何意义）。如果用计算式来表示，就是

\[\begin{bmatrix}u_1 \\u_2 \\u_3\end{bmatrix}\times\begin{bmatrix}v_1 \\v_2 \\v_3\end{bmatrix} = \det(\begin{bmatrix}\hat{i} & u_1 & v_1 \\\hat{j} & u_2 & v_2 \\\hat{k} & u_3 & v_3\end{bmatrix}) = (u_2v_3 - u_3v_2)\hat{i} + (u_3v_1 - u_1v_3)\hat{j} + (u_1v_2 - u_2v_1)\hat{k}. \]

接下来解释为什么可以这样计算。

通过二维向量合理外推：

\[\vec{u} \times \vec{v} \times \vec{w} = \ 在三维空间中张成的六面体体积，符号任然满足右手定则\ \]

但是这样定义需要有三个向量相乘，我们要定义一种两个向量相乘的运算。即\(\vec{u} \times \vec{v}\)。

这个乘积应该满足，再乘上一个三维向量w， 其积为 “在三维空间中张成的六面体体积，符号任然满足右手定则”这一原则。

六面体体积 = 底面 * 高

其底面大小是：以 u 和 v 作为临边的平行四边形的面积。

其高所在直线与该平行四边形垂直

将\(\vec{w}\)投影到高所在直线上，将\(\vec{w}\)在高这一维度的分量作为高的大小。

再回忆一下其几何定义： 当两个三维空间中的向量 u 和 v 做叉积时，可以得到另一个向量 ，满足这个向量的模长为以 u 和 v 作为临边的平行四边形的面积，垂直于这个平行四边形，且满足右手定则。

这个定义就满足了：再乘上一个三维向量w， 其积为 “在三维空间中张成的六面体体积，符号任然满足右手定则”

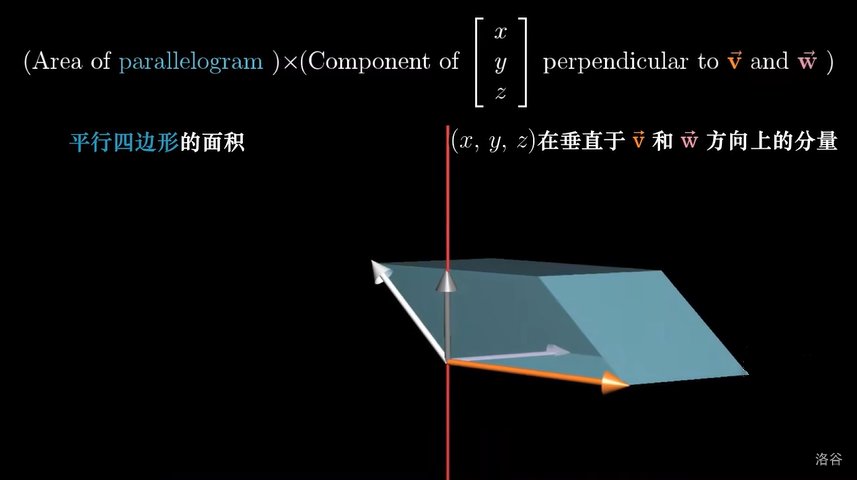
例子

假设我们有两个向量 a=(1,2,3) 和 b=(4,5,6)。

1. 计算点积：a⋅b=1⋅4+2⋅5+3⋅6=4+10+18=32

2. 计算叉积：a×b=(2⋅6−3⋅5,3⋅4−1⋅6,1⋅5−2⋅4)=(12−15,12−6,5−8)=(−3,6,−3)

因此，点积的结果是 32，叉积的结果是 (−3,6,−3)。

特征向量和特征值

对于一个线性变换，总有一些向量在变换前后方向不发生改变，这些向量就是特征向量。

但是特征向量在变化 前后的模长会发生等比例变化，变动的倍数k，就是特征值。

以斐波那契数列对应的矩阵为例（矩阵就是线性变换）：

\[\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} f_{i-1} \\ f_{i-2} \end{bmatrix} = \begin{bmatrix} f_i \\ f_{i-1} \end{bmatrix}. \]

假设矩阵\(\begin{bmatrix}1 & 1 \\1 & 0\end{bmatrix}\)对应的特征向量为\(\begin{bmatrix}a\\b\end{bmatrix}\)，则：

\[\begin{bmatrix}1 & 1 \\1 & 0\end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix} = v\begin{bmatrix}a\\b\end{bmatrix}\\ \therefore \left\{\begin{matrix} a + b = va\\ a = vb \end{matrix}\right. \Rightarrow v = \frac{1 \pm \sqrt 5}{2} \]

这表明2*2的线性变换有两对特征值，还有很多个特征向量。其中一个特征向量为\(\begin{bmatrix}1 - \sqrt{5} \\2\end{bmatrix}\)

基变换

如果让一个向量做线性变换时只改变其长度而不改变其方向，可以有一些优良性质（例如用于求矩阵通项公式）。

于是我们想到特征向量刚好就不会改变方向。

所以我们先变到两个特征向量张成的空间中，再成上对角线是特征值的对角矩阵，最后再变回原来的空间中。

例如：

\[\begin{bmatrix}1 & 1 \\1 & 0\end{bmatrix} = \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right] \left[\begin{matrix}\frac{\sqrt{5}+1}{2} & 0 \\0 & \frac{1-\sqrt{5}}{2}\end{matrix}\right] \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right]^{-1} \]

线性代数的应用

本蒟蒻只知道可以用来求矩阵的通项公式，这里还是以斐波那契的转移矩阵为例：

\[\begin{bmatrix}1 & 1 \\1 & 0\end{bmatrix} \begin{bmatrix}f_{i-1} \\f_{i-2}\end{bmatrix} = \begin{bmatrix}f_i \\f_{i-1}\end{bmatrix}. \\ \begin{bmatrix}1 & 1 \\1 & 0\end{bmatrix} ^ {n-1} \begin{bmatrix}f_{1} \\f_{2}\end{bmatrix} =\begin{bmatrix}f_n \\f_{n-1}\end{bmatrix}. \\ \because f_1 = f_2 = 1 (初始值)\\ \therefore( \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right] \left[\begin{matrix}\frac{\sqrt{5}+1}{2} & 0 \\0 & \frac{1-\sqrt{5}}{2}\end{matrix}\right] \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right]^{-1} )^{n-1} \begin{bmatrix}1 \\1 \end{bmatrix} = \begin{bmatrix}f_n \\f_{n-1}\end{bmatrix}. \\\because( \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right] \left[\begin{matrix}\frac{\sqrt{5}+1}{2} & 0 \\0 & \frac{1-\sqrt{5}}{2}\end{matrix}\right] \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right]^{-1} )^{n-1} = \\ \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right] \left[\begin{matrix}\frac{\sqrt{5}+1}{2} & 0 \\0 & \frac{1-\sqrt{5}}{2}\end{matrix}\right] \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right]^{-1} \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right] \left[\begin{matrix}\frac{\sqrt{5}+1}{2} & 0 \\0 & \frac{1-\sqrt{5}}{2}\end{matrix}\right] \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right]^{-1}...^{n-1个}... \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right] \left[\begin{matrix}\frac{\sqrt{5}+1}{2} & 0 \\0 & \frac{1-\sqrt{5}}{2}\end{matrix}\right] \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right]^{-1} \]

\[\\\because AA^{-1} = I \\\therefore 上式= \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right] \left[\begin{matrix}\frac{\sqrt{5}+1}{2} & 0 \\0 & \frac{1-\sqrt{5}}{2}\end{matrix}\right]^{n-1} \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right]^{-1} \\\because \left[\begin{matrix}\frac{\sqrt{5}+1}{2} & 0 \\0 & \frac{1-\sqrt{5}}{2}\end{matrix}\right]^{n-1} = \left[\begin{matrix}(\frac{\sqrt{5}+1}{2})^{n-1} & 0 \\0 & (\frac{1-\sqrt{5}}{2})^{n-1}\end{matrix}\right] \\\therefore \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right] \left[\begin{matrix}(\frac{\sqrt{5}+1}{2})^{n-1} & 0 \\0 & (\frac{1-\sqrt{5}}{2})^{n-1}\end{matrix}\right] \left[\begin{matrix}1+\sqrt{5} & 1-\sqrt{5} \\2 & 2\end{matrix}\right]^{-1} \begin{bmatrix}1 \\1 \end{bmatrix} = \begin{bmatrix}f_n \\f_{n-1}\end{bmatrix}. \]

通过高斯消元求逆和暴力合并左边的所有矩阵：

\[\frac{\sqrt{5}}{5} \begin{bmatrix} \left(\frac{\sqrt{5}+1}{2}\right)^n - \left(\frac{1-\sqrt{5}}{2}\right)^n \\ \left(\frac{\sqrt{5}+1}{2}\right)^{n-1} - \left(\frac{1-\sqrt{5}}{2}\right)^{n-1} \end{bmatrix} = \begin{bmatrix} f_n \\ f_{n-1} \end{bmatrix} \]

所以fn的通项公式就是：

\[f_n = \frac{\sqrt{5}}{5} \left[ \left( \frac{\sqrt{5}+1}{2} \right)^n - \left( \frac{1-\sqrt{5}}{2} \right)^n \right] \]

（因为是大佬JPGOJCZX给我讲的线性代数，所以很多内容都参考了他的博客）