线性代数学习笔记(一):线性代数基础知识
向量
定义
从偏计算机的角度分析,这是排成一列的数。
从偏物理的角度分析,这是一条有方向有长度的线段。
可以通过数形结合的方式来理解向量。
向量的表示法:
虽然向量的起点不固定,但画平面直角坐标系中的向量,我们一般将向量的起点放在 \((0, 0)\),用向量的终点表示这个向量,如图:
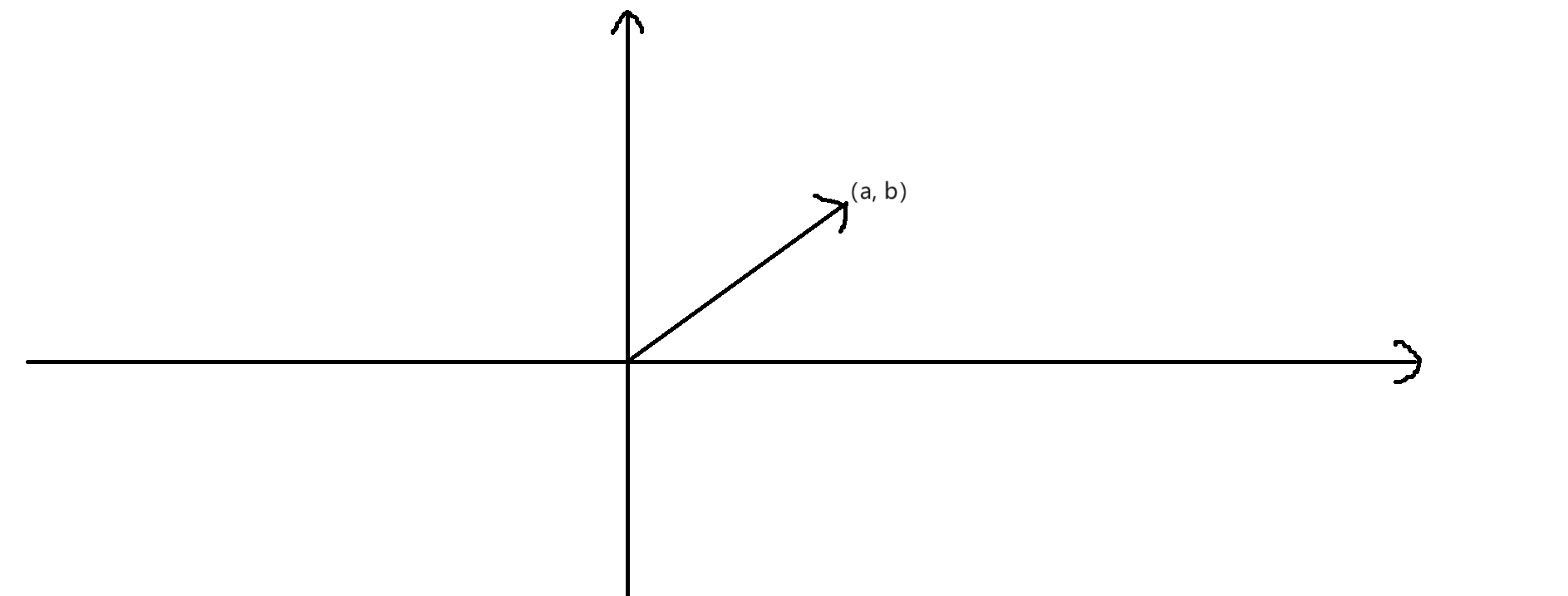
这个向量可以表示成 \((a, b)\),用计算机的表现方式,也可以写作 \(\begin{bmatrix} a \\b\end{bmatrix}\)
模长:向量 \(\begin{bmatrix} a \\b\end{bmatrix}\) 的长度;
零向量:模长为 \(0\) 的向量;
单位向量:模长为 \(1\) 的向量。
运算
基
其实,任何一个向量 \(\overrightarrow{v}\) 的坐标表示 \((a, b)\),都可以表示成 \(v = a \hat{i} + b \hat{j}\),其中 \(\hat{i}\) 和 \(\hat{j}\) 分别是 \(x\) 轴和 \(y\) 轴方向上的单位向量。
观察到,平面中的所有向量都可以表示成 \(\hat{i}\) 和 \(\hat{j}\) 的线性组合,此时 \(\hat{i}\) 和 \(\hat{j}\) 就称作这个平面的一组基。注意到,只要是非共线的两个向量,都可以作为这个平面的一组基。而共线的两个向量,只能作为它们所在直线的一组基。
扩展而言,非共面的三个向量 \(\hat{i}\)、\(\hat{j}\) 和 \(\hat{k}\) 可以作为空间的一组基,共面不共线的 \(3\) 个向量可以作为平面的一组基,更高维空间同理。
张成空间
如果 \(\hat{i}\) 和 \(\hat{j}\) 是这个平面的一组基,那么这个平面就叫做这两个向量的张成空间,更高维空间同理。
矩阵
\(\text{Unfortunately, no one can be told what the Matrix is.}\)
\(\text{You have to see it for yourself.}\)
\(\text{—— Morpheus, The Matrix}\)
定义
由 \(n \times m\) 个数 \(a_{i, j}\) 排成的 \(n\) 行 \(m\) 列的数表称为 \(n\) 行 \(m\) 列的矩阵 \(A\),简称 \(n \times m\) 矩阵 \(A\)。记作:
单位矩阵(对角矩阵):一个 \(n \times n\) 的矩阵 \(I\),除了对角线上的数为 \(1\),其他位置全为 \(0\) 那么这个矩阵就被叫做单位矩阵:
运算
-
加法:一个 \(n \times m\) 的矩阵 \(A\),加上一个 \(n \times m\) 的矩阵 \(B\),得到一个 \(n \times m\) 的矩阵 \(C\),其中 \(c_{i, j} = a_{i, j} + b_{i, j}\);
-
乘法:一个 \(n \times p\) 的矩阵 \(A\),乘以一个 \(p \times m\) 的矩阵 \(B\),得到一个 \(n \times m\) 的矩阵 \(C\),其中 \(c_{i, j} = \displaystyle\sum_{k = 1}^p a_{i, k} b_{k, j}\)。
其实矩阵乘法是一个很反直觉的事情,应为按理说矩阵乘法也应该像矩阵加法一样,对应位置相乘。但现实中的矩阵乘法确实 \(A\) 的每一排与 \(B\) 的每一列对应位置相乘再相加,这其实得从矩阵的来源讲起。
其实矩阵一开始是用来简化表示多元一次方程组的,比如以下二元一次方程方程组:
将它改写成矩阵形式:
此时是一个矩阵乘以一个向量的形式,可以初步感受到矩阵乘法的法则是对的。
下面考虑将 \(a_{1, 1}x + a_{1, 2}y\) 看做一个整体,\(a_{2, 1}x + a_{2, 2}y\) 看做一个整体,再继续往上累积系数:
重新整理 \(x, y\) 可得:
将原式改写成矩阵形式:
可以发现,如果运用矩阵乘法,乘出来的矩阵再变为二元一次方程组的形式,会和整理后的方程一模一样,这也是为什么矩阵乘法要这样定义了。
- 转置:一个 \(n \times m\) 的矩阵 \(A\),转置成一个 \(m \times n\) 的矩阵 \(B\),其中 \(B_{i, j} = A_{j, i}\)
逆
对于一个矩阵 \(A\),如果存在一个矩阵 \(B\),使得 \(BA = I\),那么称 \(B\) 为 \(A\) 的逆矩阵,具体求法在高斯消元时再来整理。
线性变换
线性变换是一个由一个向量映射到另一个向量的函数,满足:
-
原本终点同一条直线上的向量变换后终点仍在同一条直线上;
-
原来的零向量变换后还是零向量。
注意到,在线性变换中,一个向量的不同部分的缩放比是相同的,否则会将之前的直线变为曲线,比如离原点越远,放大比例就越大的变换:
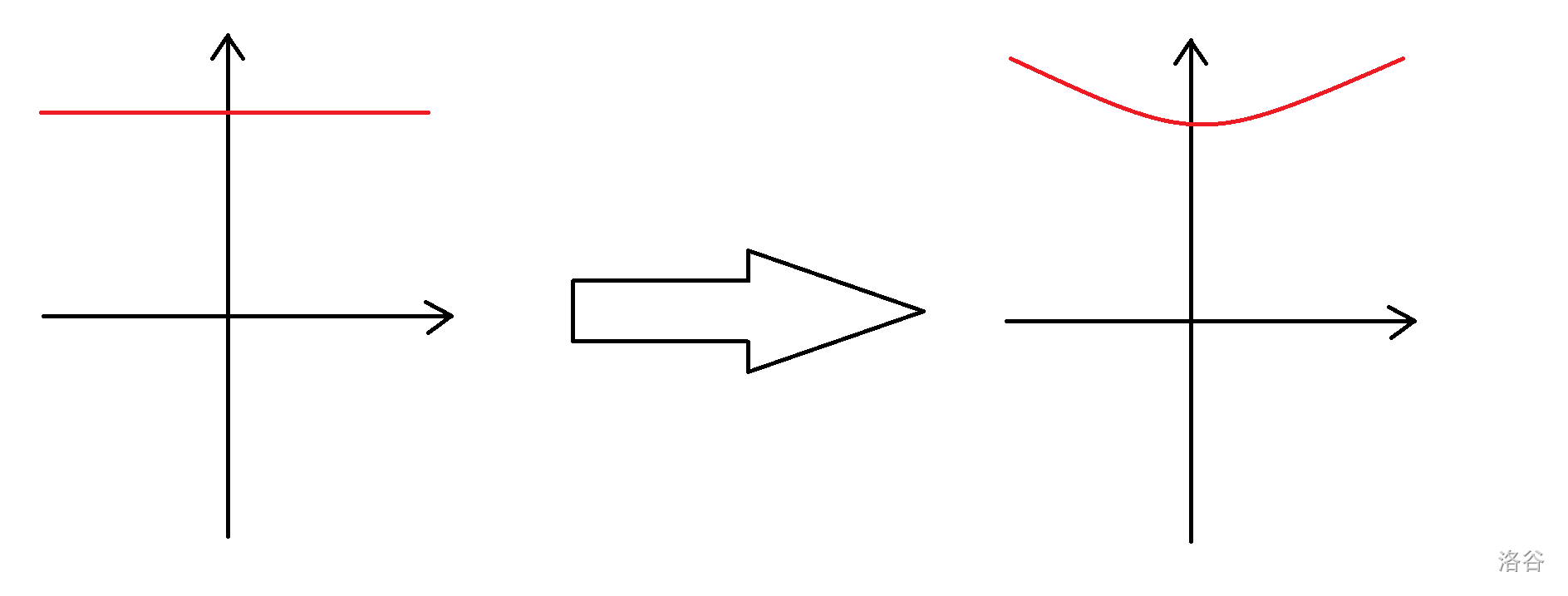
这种变换会形成曲线,因此不是线性变换。
而剪切这种变换,将横着的线段不变化,竖着的线段顺时针倾斜 \(45^{\circ}\):


这种变换符合线性变换的性质,因此剪切变换是线性变换。
由于一个向量不同部分的缩放比相同,因此如果 \(v = a \hat{i} + b \hat{j}\),那么一定可以找到这个平面新的一组基 \(\hat{i}'\) 和 \(\hat{j}'\),使得 \(v\) 经过该线性变换后得到的 \(v' = a \hat{i}' + b \hat{j}'\)(在剪切变换中,\(\hat{i}' = \begin{bmatrix} 1 \\ 0\end{bmatrix}\),\(\hat{j}' = \begin{bmatrix} 1 \\ 1\end{bmatrix}\)),那么如果我们将新得到的两个基写在一起,成为一个 \(2 \times 2\) 的矩阵(剪切变换中为 \(\begin{bmatrix} 1 & 1 \\ 0 & 1\end{bmatrix}\)),那么我们就可以用矩阵表示一个线性变换,这也可以说明矩阵乘法具有结合律。
行列式
我们讲到,在线性变换中,向量的模长与方向都发生了变化,那么平面上的所有正方形的面积都发生了变化,如果把正方形的大小变得无限接近于 \(0\),那么平面上任何一个图形都可以看做由这些小正方形组成,因此它们面积的变化都一样,而行列式正是用来刻画面积变换的一个函数。
记一次线性变换的面积变化为 \(| \det(A) |\),其中 \(\det(A)\) 的正负由平面是否翻转决定(可以感性理解一下),它的计算式为 \(\det(A) = \displaystyle\sum_{\pi}(-1)^{r(\pi)}\displaystyle\prod_{i=1}^n M_{i, \pi_i}\),其中 \(\pi\) 表示任意一个 \(1\) 到 \(n\) 的排列,而 \(r(\pi)\) 则是 \(\pi\) 的逆序对数量。
其实对于二维空间,\(n\) 的排列只有 \(\{1, 2\}\) 和 \(\{2, 1\}\) 两种,那么行列式的计算可以简化成 \(\det(\begin{bmatrix} a & b \\ c & d\end{bmatrix}) = ad - bc\),可以根据大佬zwfymqz的博客中的图片:
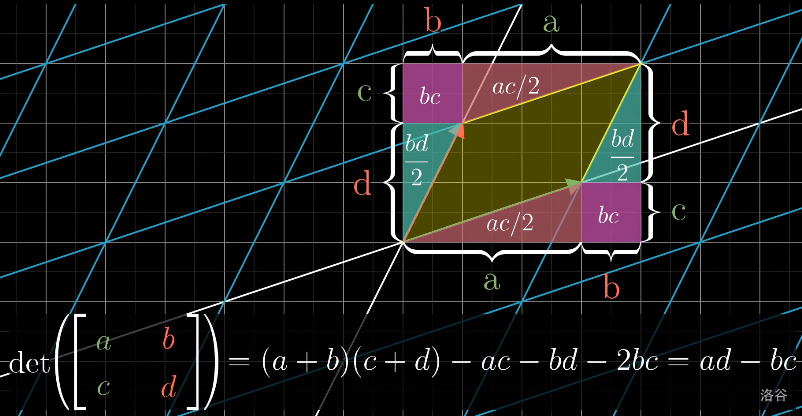
来理解。接着你会发现中小学的新定义运算中的一类经典题其实就是在求二维矩阵的行列式,原来我小学就会线性代数了啊。
当 \(\det(M) = 0\) 时,也就是说这个变换使得小正方形的面积变为了 \(0\)(比如映射到了同一条直线上),此时这个变换一定使空间的某一维发生了坍缩。反过来,若一个变换使得空间的某一维发生了坍缩,那么这个变换的行列式一定为 \(0\)。
行列式有一个重要的性质:\(\det(M_1)\det(M_2) = \det(M_1M_2)\),可以理解为先将“小正方形的面积”扩大 \(k_1\),再将“小正方形的面积”扩大 \(k_2\),相当于将“小正方形的面积”扩大了 \(k_1k_2\) 倍,这在求初等变换的某些性质时很有用。
列空间
我们知道一个线性变换可以通过将变换后的基拼在一起成为一个矩阵来表示,而这一组基张成的空间就成为这个矩阵的列空间。
这与之前介绍的矩阵与线性方程组的关系有所联系,如果等式右边的答案向量不在该系数矩阵的列空间中,那么这个线性方程组就是无解的,因为无论如何都找不到一个向量,在进行该线性变换后,可以得到答案向量。
秩
一个线性变换的列空间的维度,如果一个线性变换前的秩与变换后的秩没发生变化,那么该线性变换就未造成空间的坍缩,否则该线性变换就使空间的某些维坍缩了。
如果一个变换的秩是该变换能达到的最大的秩,那么就称该线性变换的矩阵是满秩的,比如一个 \(2 \times 2\) 的矩阵,如果它的秩是 \(2\),那么他就是满秩的。
零空间
如果一个线性变换使空间的某一维坍缩了,那么会有一些向量被映射到了原点,这些向量组成的空间就是零空间。零空间可以用来表示一个线性方程组解的个数。
点积
定义两个向量 \(u = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}\) 和 \(v = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}\) 的点积为 $u \cdot v = x_1 \cdot y_1 + x_2 \cdot y_2 + \dots + x_n \cdot y_n $,乍一看长相平平,但其实向量的点积与线性变换有紧密的联系,这也是为什么放在线性变换来讲,而不是向量的原因。
其实,点积有它的几何性质,如图:
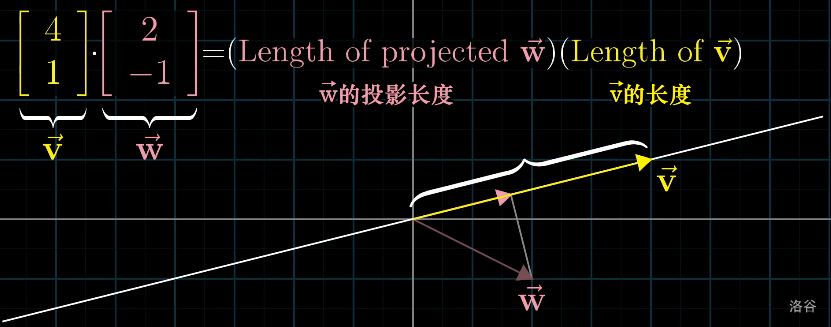
两个向量的点积,等于一个向量 \(w\) 在另一个向量 \(v\) 上的投影的长度与 \(v\) 的模长的乘积。
很显然,如果 \(w\) 在 \(v\) 上的投影与 \(v\) 的方向相同,那么点积为正,否则点积为负。
下面我们来证明为什么是这样的。
考虑到两个向量的乘积变成了一个数字,其实是发生了空间的坍缩,而这恰好可以用矩阵来表示,那么现在就需要找到一个从二维空间到一维空间的线性变换。
首先,由于该线性变换的秩是 \(1\),也就是说列空间的维度是 \(1\),那必然 \(\hat{i}'\) 和 \(\hat{j}'\) 也只是一个数,可以用 \(\begin{bmatrix} a & b \end{bmatrix}\) 来表示。
考虑到一维空间就是一条数轴,那么我们可以将数轴放上平面直角坐标系,记这条数轴的的基为 \(\hat{u}\),为了方便,假设它的模长为 \(1\):
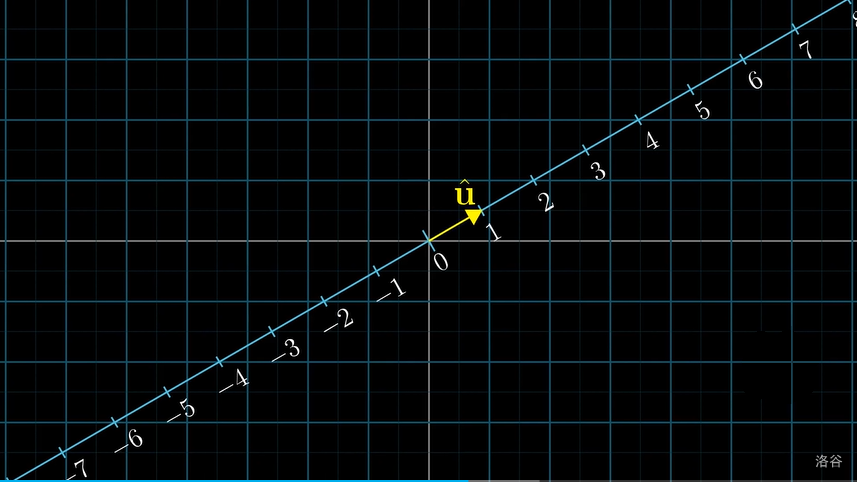
那么此时,平面上的任何一个点,往这条数轴作垂线,都可以得到一个数:
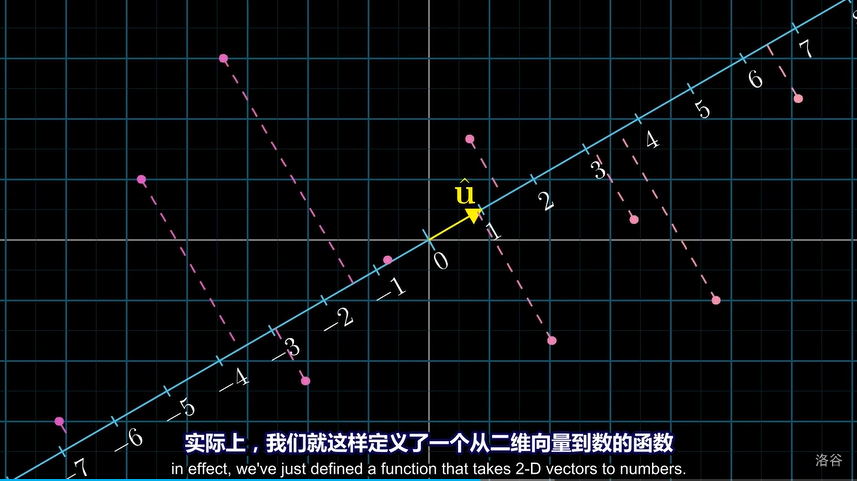
这时,我们其实已经发现这个变换了,现在考虑的就是如何将 \(\hat{u}\) 用 \(\hat{i}\) 和 \(\hat{j}\) 来表示,这样就可以得到线性变换的矩阵了。我们发现其实可以构造出一对对称性的全等三角形:
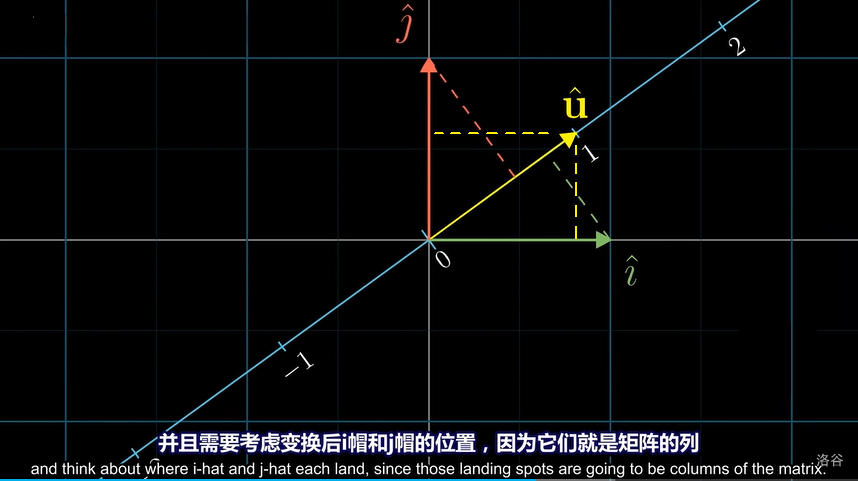
现在来考虑变换后的 \(\hat{i}\) 和变换后的 \(\hat{j}\) 分别是什么。根据这两组全等三角形,我们可以发现 \(\hat{i}\) 变成了 \(\hat{u}\) 的横坐标,\(\hat{j}\) 变成了 \(\hat{u}\) 的纵坐标,那么这个线性变换就能表示成 \(\begin{bmatrix} \hat{u}_x & \hat{u}_y \end{bmatrix}\),现在你会惊奇的发现,这个矩阵乘上一个向量,就等于 \(\hat{u}\) 与这个向量进行点乘。那么这时一个向量 \(\hat{v}\) 与 \(\hat{u}\) 点乘,也就相当于将 \(\hat{u}\) 投影到数轴上,也就是 \(\hat{u}\) 所在的直线上。
现在考虑模长不是 \(1\) 的向量 \(s\),那么 \(s\) 可以表示成 \(a \hat{u}\),\(a\) 为 \(s\) 的模长,那么此时的线性变换矩阵就可以写成 \(\begin{bmatrix} a \hat{u}_x & a \hat{u}_y \end{bmatrix} = a\begin{bmatrix} \hat{u}_x & \hat{u}_y \end{bmatrix}\)。此时,如果一个向量 \(t\) 要与 \(s\) 点乘,那么相当于要先将 \(t\) 投影到 \(s\) 所在的直线,再将投影的长度与 \(s\) 的模长相乘,此时点积的几何意义证明成立。
其实,点积是存在交换律的,可以计算证明,也可以通过射影定理证明,此处不再赘述。
叉积
定义向量 \(u\) 和 \(v\) 的叉积 \(u \times v\) 为以 \(u\) 和 \(v\) 作为临边的平行四边形的面积,叉积的值可以通过行列式求出。
可以发现,由于行列式可正可负,因此叉积的值也可正可负,这取决于平面是否翻转。如果 \(u\) 与 \(v\) 进行叉积,则 \(u \times v\) 为正,\(v \times u\) 为负。
事实上,狭义的叉积只对三维空间有用。当两个三维空间中的向量 \(u\) 和 \(v\) 做叉积时,可以得到另一个向量 \(w\),满足这个向量的模长为以 \(u\) 和 \(v\) 作为临边的平行四边形的面积,垂直于这个平行四边形,且满足右手定则。如果用计算式来表示,就是 \(\begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} \times \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} = \det(\begin{bmatrix} \hat{i} & u_1 & v_1 \\ \hat{j} & u_2 & v_2 \\ \hat{k} & u_3 & v_3\end{bmatrix}) = (u_2v_3 - u_3v_2)\hat{i} + (u_3v_1 - u_1v_3)\hat{j} + (u_1v_2 - u_2v_1)\hat{k}\),接下来证明为什么可以这样计算。
我们先假设不知道如何计算两个三维向量的叉积,此时,通过二维空间两个向量的叉积合理外推,三维空间的叉积应该需要三个向量 \(u, v, w\),它们的叉积 \(u \times v \times w\) 表示以 \(u, v, w\) 作为临边的平行六面体的体积,此时可以用 \(\det(\begin{bmatrix} u_1 & v_1 & w_1 \\ u_2 & v_2 & w_2 \\ u_3 & v_3 & w_3 \end{bmatrix})\) 来表示。
这时我们把 \(u\) 这个向量当做主元,将叉积看做一个函数,此时可以得到 \(f(\begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix}) = \det(\begin{bmatrix} u_1 & v_1 & w_1 \\ u_2 & v_2 & w_2 \\ u_3 & v_3 & w_3 \end{bmatrix})\),可以发现这是一个从三维向量到一位向量的线性变换,因此仿照点积,这个函数可以写作 \(\begin{bmatrix} x & y & z \end{bmatrix}\begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} = \det(\begin{bmatrix} u_1 & v_1 & w_1 \\ u_2 & v_2 & w_2 \\ u_3 & v_3 & w_3 \end{bmatrix})\),又可以写成 \(\begin{bmatrix} x \\ y \\ z \end{bmatrix} \cdot \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} = \det(\begin{bmatrix} u_1 & v_1 & w_1 \\ u_2 & v_2 & w_2 \\ u_3 & v_3 & w_3 \end{bmatrix})\)。现在我们就需要找到这个向量 \(p\)。
从计算的角度思考,等式左边为 \(xu_1 + yu_2 + zu_3\),等式右边为 \((v_2w_3 - v_3w_2)u_1 + (v_3w_1 - v_1w_3)u_2 + (v_1w_2 - v_2w_1)z\),此时我们已经可以求出这个向量,现在我们发现这个向量其实与 \(u\) 没有任何关系,于是如果 \(u = \begin{bmatrix} \hat{i} \\ \hat{j} \\ \hat{k} \end{bmatrix}\),对 \(p\) 的取值也无影响。因此这里的 \(\hat{i}, \hat{j}, \hat{k}\) 只是为了方便计算,并无实际意义。
接着来求解叉积的几何性质。
首先,我们知道点积是将一个向量投影到另一个向量上,再乘以这个向量的模长。
现在,我们知道,\(p\) 与 \(u\) 的点积,等于以 \(u\),\(v\),\(w\) 为临边的平行六面体的体积,由于平行六面体的体积等于底面面积乘以高,于是不妨将 \(u\) 投影到垂直于 \(v\) 和 \(w\) 的直线上:
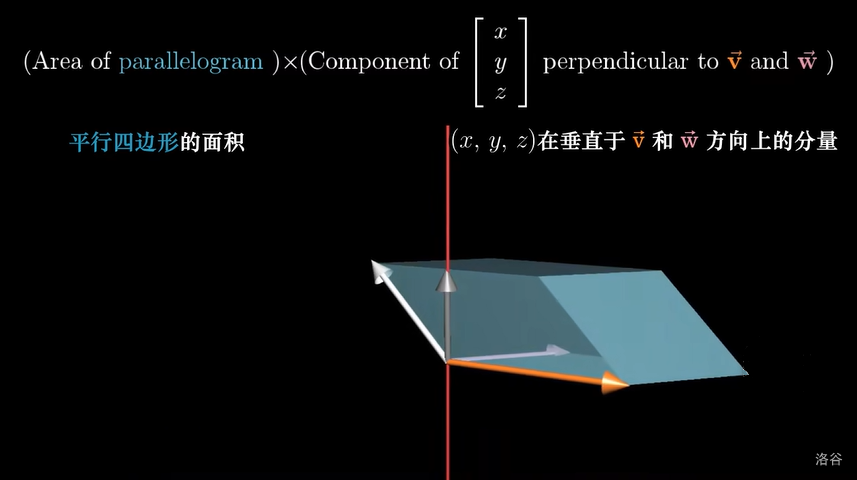
那么,这个平行六面体的体积就等于底面积与投影的积,而这正好等于 \(u\) 与垂直于 \(v\) 和 \(w\) 且模长等于底面积的向量的点积,因此 \(p\) 的几何性质得以证明。
特征向量与特征值
定义一个线性变换 \(M\),如果存在一个向量 \(v\) 和一个常数 \(a\) 使得 \(Mv = av\),那么就称 \(v\) 为 \(M\) 这个线性变换的特征向量,\(a\) 为这个变换的特征值。
可以发现 \(v\) 这个向量在 \(M\) 变换中只发生了模长的变化,因此可以比较准确的刻画 \(v\) 的变化,也方便计算矩阵的幂。
以斐波那契数列为例。首先,斐波那契数列的递推公式为 \(f_1 = f_2 = 1, f_i = f_{i - 1} + f_{i - 2}(i > 1)\),可以写成 \(f_i = 1 \times f_{i - 1} + 1 \times f_{i - 2}\),而 \(f_{i - 1}\) 又可以写成 \(f_{i - 1} = 1 \times f_{i - 1} + 0 \times f_{i - 2}\),发现这和矩阵乘法很类似,于是将其改写成矩阵形式为 \(\begin{bmatrix} f_{i - 1} \\ f_{i - 2} \end{bmatrix}\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} f_i \\ f_{i - 1} \end{bmatrix}\)。
假设特征向量 \(v = \begin{bmatrix} x \\ y\end{bmatrix}\),那么 \(Mv = av\),发现这个式子硬解有 \(3\) 个未知数,但只有两个方程,考虑把 \(av\) 变成一个矩阵乘以一个向量的形式,也就是 \(\begin{bmatrix} a & 0 \\ 0 & a\end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix}\),将此式移到等号左边,再进行矩阵减法,可以得到 \(\begin{bmatrix} 1 - a & 1 \\ 1 & - a\end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix} = 0\)。
显然,当 \(x = y = 0\) 时等式成立,但这很没有意思,靠虑当 \(x\) 和 \(y\) 中最多有 \(1\) 个 \(0\) 时,可以发现该变换将一条直线映射到了一个点,发生了维度的坍缩,依据行列式的结论,此时 \(\det(\begin{bmatrix} 1 - a & 1 \\ 1 & -a\end{bmatrix})\) 一定为 \(0\),即 \(-a(1 - a) - 1 = 0\),整理得 \(a^2 - a - 1 = 0\),解得 \(a_1 = \displaystyle\frac{1 + \sqrt 5}{2}, a_2 = \frac{1 - \sqrt 5}{2}\),证明每进行一次 \(M\) 变换,有一个特征向量的长度变为了原先的 \(\displaystyle\frac{1 + \sqrt 5}{2}\),另一个变为了原先的 \(\displaystyle\frac{1 - \sqrt 5}{2}\)。
接下来求解特征向量,将 \(a = \displaystyle\frac{1 + \sqrt 5}{2}\) 带入原先的等式 \(Mv = av\),得到 \(\begin{cases} x + y = \displaystyle\frac{1 + \sqrt 5}{2}x \\ x = \displaystyle\frac{1 + \sqrt 5}{2}y\end{cases}\),但这会解出无穷多组解,因为在某个特征向量所在直线上的所有向量在 \(M\) 变换中都只发生模长的变化,就以 \(\begin{bmatrix} 1 + \sqrt 5 \\ 2 \end{bmatrix}\) 为例。
同理,可以求出另一个特征向量 \(\begin{bmatrix} 1 - \sqrt 5 \\ 2 \end{bmatrix}\)。
基变换
有些时候,我们用的基是 \(\hat{i}\) 和 \(\hat{j}\),并通过这一组基的线性组合来表示其他向量,但题目中的一个向量可能是通过另一组基 \(\hat{u}\) 和 \(\hat{v}\) 的线性组合来表示的,这时我们就需要通过基变换来将此向量用 \(\hat{i}\) 和 \(\hat{j}\) 来表示。
假设 \(\hat{u}\) 和 \(\hat{v}\) 在 \(\hat{i}\) 和 \(\hat{j}\) 的张成空间中表示为 \(p \hat{i} + q \hat{j}\) 和 \(s \hat{i} + t \hat{j}\),\(x\) 在 \(\hat{u}\) 和 \(\hat{v}\) 的张成空间中表示为 \(a \hat{u} + b \hat{v}\),那么其实 \(x = (ap + bs) \hat{i} + (aq + bt)\hat{j}\),更近一步说就是 \(\begin{bmatrix} a \\ b \end{bmatrix}\) 左乘上了 \(\begin{bmatrix} p & s \\ q & t \end{bmatrix}\),这时我们就可以把用别的基表示的向量变换到需要用的基中来。
当我们需要把别的基中的向量运用当前基的线性变换时,只需要乘上 \(\begin{bmatrix} p & s \\ q & t \end{bmatrix}\) 将该向量转到当前基中,进行线性变换后再乘上 \(\begin{bmatrix} p & s \\ q & t \end{bmatrix}^{-1}\) 把变换后的向量再转到别的基就可以了。形式化的,如果要把以 \(\hat{u}\) 和 \(\hat{v}\) 为基的向量在当前基中进行剪切变换,那么需要求的就是 \(\begin{bmatrix} p & s \\ q & t \end{bmatrix}^{-1} \begin{bmatrix} 1 & 1 \\ 0 & 1\end{bmatrix} \begin{bmatrix} p & s \\ q & t \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix}\)。
这就是基变换的基础知识,它最直接的应用就是求递推函数的通项公式,下面以斐波那契数列为例。
求递推函数通项公式
我们知道斐波那契数列的转移矩阵是 \(\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}\),已经可以用矩阵快速幂来做了,但发现这个式子很像一个线性变换的式子。其实可以发现,把初始的矩阵 \(a = \begin{bmatrix} f_2 \\ f_1 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}\) 进行 \(n - 2\) 次 \(M = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}\) 变换,答案就为向量的第一个数字,但你会发现,进行一次该变换后,该向量的方向和模长都发生了变化,使得很难准确刻画该变换,这时我们就需要特征值与特征向量的帮忙。
我们已经知道了斐波那契数列的转移矩阵的特征向量是 \(\begin{bmatrix} 1 + \sqrt 5 \\ 2 \end{bmatrix}\) 和 \(\begin{bmatrix} 1 - \sqrt 5 \\ 2 \end{bmatrix}\),考虑以 \(\begin{bmatrix} 1 + \sqrt 5 \\ 2 \end{bmatrix}\) 和 \(\begin{bmatrix} 1 - \sqrt 5 \\ 2 \end{bmatrix}\) 作为基,那么基变换矩阵 \(A\) 就是 \(\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix}\),由于 \(M\) 这个变换在 \(A\) 中这一组基就只有模长的变化,而模长的变化正好是特征值,因此 \(M\) 就可以写成 \(\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} \displaystyle\frac{\sqrt 5 + 1}{2} & 0 \\ 0 & \displaystyle\frac{1 - \sqrt 5}{2} \end{bmatrix}\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix}^{-1}\)。
变换 \(1\) 次是 \(Ma\),那么可以改写成 \(\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} \displaystyle\frac{\sqrt 5 + 1}{2} & 0 \\ 0 & \displaystyle\frac{1 - \sqrt 5}{2} \end{bmatrix}\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix}^{-1}a\)。
变换 \(n - 2\) 次,就可以得到 \((\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix} \begin{bmatrix} \displaystyle\frac{\sqrt 5 + 1}{2} & 0 \\ 0 & \displaystyle\frac{1 - \sqrt 5}{2} \end{bmatrix}\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix}^{-1})^{n - 2}a\)
将逆矩阵求出来,原式就变成了 \((\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix}\begin{bmatrix} \displaystyle\frac{\sqrt 5 + 1}{2} & 0 \\ 0 & \displaystyle\frac{1 - \sqrt 5}{2} \end{bmatrix}\begin{bmatrix} \displaystyle\frac{\sqrt 5}{10} & \displaystyle\frac{5 - \sqrt 5}{20} \\ -\displaystyle\frac{\sqrt 5}{10} & \displaystyle\frac{5 + \sqrt 5}{20} \end{bmatrix})^{n - 2}a\)
由于 \(A M' A^{-1} \times A M' A^{-1} = A M'^2 A^{-1}\),那么原式就会变成 \(\begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix}\begin{bmatrix} (\displaystyle\frac{\sqrt 5 + 1}{2})^{n - 2} & 0 \\ 0 & (\displaystyle\frac{1 - \sqrt 5}{2})^{n - 2} \end{bmatrix}\begin{bmatrix} \displaystyle\frac{\sqrt 5}{10} & \displaystyle\frac{5 - \sqrt 5}{20} \\ -\displaystyle\frac{\sqrt 5}{10} & \displaystyle\frac{5 + \sqrt 5}{20} \end{bmatrix}a\)
接着进行普通的矩阵乘法,那么原式
\( \begin{aligned} &= \begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix}\begin{bmatrix} (\displaystyle\frac{\sqrt 5 + 1}{2})^{n - 2} & 0 \\ 0 & (\displaystyle\frac{1 - \sqrt 5}{2})^{n - 2} \end{bmatrix}\begin{bmatrix} \displaystyle\frac{5 + \sqrt 5}{20} \\ \displaystyle\frac{5 - \sqrt 5}{20}\end{bmatrix} \\&= \begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix}\begin{bmatrix}(\displaystyle\frac{\sqrt 5 + 1}{2})^{n - 2} \frac{5 + \sqrt 5}{20} \\ (\displaystyle\frac{1 - \sqrt 5}{2})^{n - 2} \frac{5 - \sqrt 5}{20}\end{bmatrix} \\&= \begin{bmatrix} 1 + \sqrt 5 & 1 - \sqrt 5 \\ 2 & 2 \end{bmatrix} \displaystyle\frac{\sqrt 5}{10}\begin{bmatrix}(\displaystyle\frac{\sqrt 5 + 1}{2})^{n - 1} \\ -(\displaystyle\frac{1 - \sqrt 5}{2})^{n - 1}\end{bmatrix} \\&= \displaystyle\frac{\sqrt 5}{10} \begin{bmatrix} (1 + \sqrt 5)(\displaystyle\frac{\sqrt 5 + 1}{2})^{n - 1} - (1 - \sqrt 5)(\displaystyle\frac{1 - \sqrt 5}{2})^{n - 1} \\ 2(\displaystyle\frac{\sqrt 5 + 1}{2})^{n - 1} - 2(\displaystyle\frac{1 - \sqrt 5}{2})^{n - 1} \end{bmatrix} \\&= \displaystyle\frac{\sqrt 5}{5} \begin{bmatrix} (\displaystyle\frac{\sqrt 5 + 1}{2})^n - (\displaystyle\frac{1 - \sqrt 5}{2})^n \\ (\displaystyle\frac{\sqrt 5 + 1}{2})^{n - 1} - (\displaystyle\frac{1 - \sqrt 5}{2})^{n - 1} \end{bmatrix} = \begin{bmatrix} f_n \\ f_{n - 1} \end{bmatrix} \end{aligned} \)
因此,\(f_n = \displaystyle\frac{\sqrt 5}{5}[(\displaystyle\frac{\sqrt 5 + 1}{2})^n - (\displaystyle\frac{1 - \sqrt 5}{2})^n]\)
高斯消元法
初等矩阵
定义以下三种矩阵为初等矩阵:
- 倍乘矩阵:左上到右下对角线上第 \(i\) 个位置为 \(k (k \neq 0)\),对角线上其它位置全为 \(1\),非对角线位置全为 \(0\) 的矩阵:
\(\begin{bmatrix} 1 & 0 & 0 & \dots & 0 & \dots & 0\\ 0 & 1 & 0 & \dots & 0 & \dots & 0\\ 0 & 0 & 1 & \dots & 0 & \dots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \dots & k & \dots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \dots & 0 & \dots & 1\end{bmatrix}\)
它只有一个维度扩大了 \(k\) 倍,可以发现它的行列式为 \(k\)。
- 对换矩阵:将单位矩阵第 \(i\) 排第 \(i\) 列的 \(1\) 交换到第 \(j\) 列,将第 \(j\) 排第 \(j\) 列的 \(1\) 交换到第 \(i\) 列 \((i \neq j)\) 得到的矩阵:
\(\begin{bmatrix} 1 & 0 & 0 & \dots & 0 & \dots & 0 & \dots & 0\\ 0 & 1 & 0 & \dots & 0 & \dots & 0 & \dots & 0\\ 0 & 0 & 1 & \dots & 0 & \dots & 0 & \dots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \dots & 0 & \dots & 1 & \dots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \dots & 1 & \dots & 0 & \dots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \dots & 0 & \dots & 0 & \dots & 1\end{bmatrix}\)
这相当于是将两个向量对调了一下位置,此时“平面”发生了翻转,行列式为 \(-1\)。
- 倍加矩阵:将单位矩阵第 \(i\) 行第 \(j\) 列变为 \(k (k \neq 0, i \neq j)\) 所得到的矩阵:
\(\begin{bmatrix} 1 & 0 & 0 & \dots & 0 & \dots & 0 & \dots & 0\\ 0 & 1 & 0 & \dots & 0 & \dots & 0 & \dots & 0\\ 0 & 0 & 1 & \dots & 0 & \dots & 0 & \dots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \dots & 1 & \dots & k & \dots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \dots & 0 & \dots & 1 & \dots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \dots & 0 & \dots & 0 & \dots & 1\end{bmatrix}\)
此时会发现某个向量往一个方向平移了一段距离,但是“高”没有发生变化,因此行列式为 \(1\)。
初等变换
对于一个矩阵,他的初等变换有三种:
-
用一个非 \(0\) 数 \(x\) 乘以矩阵的某一行或某一列,相当于这个矩阵乘以了倍乘矩阵;
-
将矩阵某一行或某一列乘以非 \(0\) 数 \(x\),并加到另一行或列,相当于这个矩阵乘以了倍加矩阵;
-
交换矩阵的某两行或列,相当于这个矩阵乘以了对换矩阵。
这也就是平时我们在求解线性方程组的操作方程。
普通高斯消元法
首先,我们可以通过列空间判断是否有解,通过零空间判断有多少组解,这里只考虑有唯一解的情况。
由于我们知道矩阵与线性方程组有密不可分的关系,因此可以将线性方程组变化成矩阵形式:
\(\begin{bmatrix} a_{1, 1} & a_{1, 2} & \dots & a_{1, n} & \mid & c_1\\ a_{2, 1} & a_{2, 2} & \dots & a_{2, n} & \mid & c_2\\ \vdots & \vdots & \ddots & \vdots & \mid & \vdots\\ a_{n, 1} & a_{n, 2} & \dots & a_{n, n} & \mid & c_n\end{bmatrix}\)
其中 \(A\) 是系数矩阵,\(C\) 是答案矩阵。
普通高斯消元的目标是将 \(A\) 消成一个上三角矩阵,也就是只有左上-右下对角线及其上方才有值的矩阵,这样再倒着推就可以出结果。
具体做法是枚举每一列,将第 \(i\) 列的第 \(i\) 个元素作为主元,将主元下方的第 \(j\) 排的数字通过求最小公倍数的方法消去(用 double 可以直接相除,再将主元 \(i\) 行乘以这个商再将用 \(j\) 排相减)。特别的,如果主元是 \(0\),需要将主元这列不为 \(0\) 的行与主元这行交换,如果主元这一列全为 \(0\),此时该方程已经有无数多组解了,已经排除掉了。
接着从下往上递推,由于最后一排一定是 \(ax_n = c_n\) 这种形式,于是可以求出 \(x_n\),而倒数第 \(2\) 排一定是 \(bx_{n - 1} + dx_{n - 1} = c_{n - 1}\),此时又可以把 \(x_{n - 1}\) 求出来。以此类推,就可以求出所有 \(x\) 了。
完整代码:洛谷 P3389 【模板】高斯消元法
//懒得写了,我们一般都用高斯-约旦消元法
高斯-约旦消元法
此算法在普通高斯消元的基础上,从后往前将主元上方的数给消掉了,这样只用将 \(c_i\) 除以 \(a_i\) 就可以得到答案。
完整代码(来个双倍经验):洛谷 P2455 [SDOI2006] 线性方程组
#include <bits/stdc++.h>
using namespace std;
double a[105][105], eps = 1e-6;
int main(){
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n + 1; j++)
scanf("%lf", &a[i][j]);
for(int i = 1; i <= n; i++) {
int m = i;
for(int j = 1; j <= n; j++){
if(fabs(a[j][j]) > eps && j < i)
continue;
if(fabs(a[j][i]) > fabs(a[m][i]))
m = j;
}
for(int j = 1; j <= n + 1; j++)
swap(a[i][j], a[m][j]);
if(abs(a[i][i]) <= eps)
continue;
for(int j = 1; j <= n; j++)
if(j != i){
double d = a[j][i] / a[i][i];
for(int k = i; k <= n + 1; k++)
a[j][k] -= a[i][k] * d;
}
}
int key = 1;
for(int i = 1; i <= n; i++)
if(abs(a[i][i]) <= eps)
if(abs(a[i][n + 1]) > eps)
key = -1;
else if(key != -1)
key = 0;
if(key != 1){
printf("%d", key);
return 0;
}
for(int i = 1; i <= n; i++)
printf("x%d=%.2lf\n", i, a[i][n + 1] / a[i][i]);
return 0;
}
下面展示一下高斯消元两个经典应用。
行列式求值
行列式的变换
先来两个行列式特有的变换:
- 进行一次矩阵转置,行列式不变;
证明:感性理解。考虑到行列式的表达式在枚举列的排列,每列的每个数都与从另外那几列 每一列随机选出一个数相乘。由于对称性,枚举行依然会枚举到这种排列,两种枚举方式都枚举了所有排列,因此转置一次,行列式不变。
- 若矩阵有两行成比例,行列式为 \(0\);
证明:首先可以发现,将矩阵转置后,行列式不变,那么问题可以变成矩阵有两列成比例。
这就意味着这两个向量在同一条直线上,不能同时是这个空间的一组基,那么就只剩下 \(n - 1\) 个向量,发生了维度的坍缩,因此行列式为 \(0\)。
行列式也有初等变换,分别为:
- 用一个非 \(0\) 数 \(x\) 乘以矩阵的某一行或某一列,行列式也乘以 \(x\);
证明:根据 \(\det(M_1)\det(M_2) = \det(M_1M_2)\),由于倍乘矩阵的行列式为 \(k\),那么变换后的行列式就为变换后的 \(k\) 倍。
- 将矩阵某一行或某一列乘以非 \(0\) 数 \(x\),并加到另一行或列,行列式不变;
证明:倍加矩阵的行列式为 \(1\),那么变换后的行列式的值不变。
- 交换矩阵的某两行或列,行列式取反。
证明:对换矩阵的行列式为 \(-1\),那么变换后的行列式的值取反。
代数余子式
先考虑以下 \(3 \times 3\) 矩阵 \(A\):\(\begin{bmatrix} a_{1, 1} & a_{1, 2} & a_{1, 3} \\ a_{2, 1} & a_{2, 2} & a_{2, 3} \\ a_{3, 1} & a_{3, 2} & a_{3, 3} \end{bmatrix}\),我们先按照行列式的计算式将其展开为 \(\det(\begin{bmatrix} a_{1, 1} & a_{1, 2} & a_{1, 3} \\ 0 & a_{2, 2} & a_{2, 3} \\ 0 & a_{3, 2} & a_{3, 3} \end{bmatrix}) + \det(\begin{bmatrix} 0 & a_{1, 2} & a_{1, 3} \\ a_{2, 1} & a_{2, 2} & a_{2, 3} \\ 0 & a_{3, 2} & a_{3, 3} \end{bmatrix}) + \det(\begin{bmatrix} 0 & a_{1, 2} & a_{1, 3} \\ 0 & a_{2, 2} & a_{2, 3} \\ a_{3, 1} & a_{3, 2} & a_{3, 3} \end{bmatrix})\)。
根据矩阵交换两行后,行列式取反,那么原式 \(= \det(\begin{bmatrix} a_{1, 1} & a_{1, 2} & a_{1, 3} \\ 0 & a_{2, 2} & a_{2, 3} \\ 0 & a_{3, 2} & a_{3, 3} \end{bmatrix}) - \det(\begin{bmatrix} a_{2, 1} & a_{2, 2} & a_{2, 3} \\ 0 & a_{1, 2} & a_{1, 3} \\ 0 & a_{3, 2} & a_{3, 3} \end{bmatrix}) + \det(\begin{bmatrix} a_{3, 1} & a_{3, 2} & a_{3, 3} \\ 0 & a_{1, 2} & a_{1, 3} \\ 0 & a_{2, 2} & a_{2, 3} \end{bmatrix})\)。
根据行列式的计算式,每次要从每列选出行号互不相同的 \(3\) 个数,那么如果选了 \(a_{1, 1}\),就不会再选 \(a_{1, 2}\) 和 \(a_{1, 3}\);如果选了 \(a_{1, 2}\) 或 \(a_{1, 3}\),那么第一列只会选 \(a_{2, 1}\) 或 \(a_{3, 1}\),而它们都是 \(0\),对答案无贡献。因此只有选 \(a_{1, 1}\) 时才会有贡献,于是原式可以简化成 \(a_{1, 1} \det(\begin{bmatrix} a_{2, 2} & a_{2, 3} \\ a_{3, 2} & a_{3, 3} \end{bmatrix}) - a_{2, 1} \det(\begin{bmatrix} a_{1, 2} & a_{1, 3} \\ a_{3, 2} & a_{3, 3} \end{bmatrix}) + a_{3, 1}\det(\begin{bmatrix} a_{1, 2} & a_{1, 3} \\ a_{2, 2} & a_{2, 3} \end{bmatrix})\),将行列式降维了。更高维同理。
矩阵也可以按照别的列进行展开,方法类似。
现在我们就有了余子式的定义。在一个 \(n\) 阶矩阵中,我们将第 \(i\) 行和第 \(j\) 列去除得到新的矩阵的行列式为原矩阵的行列式的余子式,记为 \(\Delta'_{i, j}\)。
将 \(\det(A)\) 按每一列展开可以得到 \(\begin{aligned}\det(A) &= a_{1, 1} \Delta'_{1, 1} - a_{1, 2} \Delta'_{1, 2} + a_{1, 3} \Delta'_{1, 3} \\ &= -a_{2, 1} \Delta'_{2, 1} + a_{2, 2} \Delta'_{2, 2} - a_{2, 3} \Delta'_{2, 3} \\ &= a_{3, 1} \Delta'_{3, 1} - a_{3, 2} \Delta'_{3, 2} + a_{3, 3} \Delta'_{3, 3}\end{aligned}\)。
有强迫症的人可能旧的正负号很碍眼,于是我们又定义 \(\Delta_{i, j} = (-1)^{i + j}\Delta'_{i, j}\),于是原式又可以写成 \(\begin{aligned}\det(A) &= a_{1, 1} \Delta_{1, 1} + a_{1, 2} \Delta_{1, 2} + a_{1, 3} \Delta_{1, 3} \\ &= a_{2, 1} \Delta_{2, 1} + a_{2, 2} \Delta_{2, 2} + a_{2, 3} \Delta_{2, 3} \\ &= a_{3, 1} \Delta_{3, 1} + a_{3, 2} \Delta_{3, 2} + a_{3, 3} \Delta_{3, 3}\end{aligned}\)。
此时这里的 \(\Delta_{i, j}\) 就叫做原矩阵的行列式的代数余子式,对于一般的矩阵 \(A\),都有 \(\det(A) = \displaystyle\sum_{i = 1}^n a_{i, j} \Delta_{i, j}\)(\(j\) 为任意一列)。
考虑到矩阵转置后行列式不变,那么 \(\det(A)\) 又 \(= \displaystyle\sum_{j = 1}^n a_{i, j}\Delta_{i, j}\)(\(i\) 为任意一行)。
行列式求值
考虑到矩阵某一行如果有 \(a_{i, j} = 0\),那么它对答案就无法造成贡献,于是考虑能否把以下矩阵:
通过行列式初等变换变为以下矩阵:
那么该矩阵的行列式就可以表达为 \(a_{n, n}' \times \det(\begin{bmatrix} a_{1, 1} & a_{1, 2} & a_{1, 3} & \dots & a_{1, n}\\ a_{2, 1} & a_{2, 2} & a_{3, 3} & \dots & a_{2, n}\\ a_{3, 1} & a_{3, 2} & a_{3, 3} & \dots & a_{3, n}\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ a_{n, 1} & a_{n, 2} & a_{n, 3} & \dots & a_{n, n} \end{bmatrix})\)。
对里面的行列式继续初等变换,那么最终答案就变成了 \(\displaystyle\prod_{i = 1}^n a_{i, i}'\)。
注意到洛谷上行列式求值的模板题为任意模数,这时对要消元的两行进行辗转相减法才可以消元。
完整代码:洛谷 P7112 【模板】行列式求值
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 6e2 + 9;
int a[N][N], n, p, ans = 1, neg = 1;
signed main(){
scanf("%lld%lld", &n, &p);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
scanf("%lld", &a[i][j]);
for(int i = 1; i <= n; i++){
for(int j = i + 1; j <= n; j++){
while(a[i][i]){
int d = a[j][i] / a[i][i];
for(int k = i; k <= n; k++)
a[j][k] = ((a[j][k] - d * a[i][k]) % p + p) % p;
for(int k = 1; k <= n; k++)
swap(a[i][k], a[j][k]);
neg = -neg;
}
for(int k = 1; k <= n; k++)
swap(a[i][k], a[j][k]);
neg = -neg;
}
}
for(int i = 1; i <= n; i++)
ans = ans * a[i][i] % p;
ans *= neg;
printf("%lld\n", (ans + p) % p);
return 0;
}
矩阵求逆
首先,如果一个矩阵的行列式为 \(0\),那么矩阵就没有逆,因为这个变换相当于把一个高维空间压缩到了更低的维度,而我们无法将一个低维空间变换成高维空间,因为此时一个向量可能对应多个向量(就像你可以想象二维空间长什么样,而想象不出四维空间长什么样)。
考虑可逆矩阵 \(A\),它的逆为 \(x\),\(AX = I\),将 \(I\) 拆开变成 \((e_1, e_2, \dots, e_n)\) 这 \(n\) 个只有 \(i\) 位置为 \(1\) 的向量,将 \(X\) 拆开变成 \((x_1, x_2, \dots, x_n)\) 这 \(n\) 个向量,于是现在我们要求 一个线性方程组:
将每一行展开,都可以得到一个线性方程组,套用高斯-约旦消元法的解法,如果我们能做到以下变换:
那么 \(X = S\),将这个线性方程组综合起来,就变成了 \((A | I) \rightarrow (I | X)\) 的变换。于是只用将单位矩阵拼在一个可逆矩阵后面,将该可逆矩阵消成单位矩阵,那么拼在后面的单位矩阵就变成了这个可逆矩阵的逆。
完整代码:洛谷 P4783 【模板】矩阵求逆
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 409, MOD = 1e9 + 7;
int a[N][N << 1], n;
int extend_gcd(int a, int b, int &x, int &y){
if(b == 0){
x = 1;
y = 0;
return 0;
}
int d = extend_gcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int mod_inverse(int a, int m){
int x, y;
extend_gcd(a, m, x, y);
return (x % m + m) % m;
}
signed main(){
scanf("%lld", &n);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++)
scanf("%lld", &a[i][j]);
a[i][i + n] = 1;
}
for(int i = 1; i <= n; i++){
int maxx = i;
for(int j = i + 1; j <= n; j++)
if(a[j][i] > a[maxx][i])
maxx = j;
for(int j = 1; j <= 2 * n; j++)
swap(a[i][j], a[maxx][j]);
if(a[i][i] == 0){
printf("No Solution");
return 0;
}
int inv = mod_inverse(a[i][i], MOD);
for(int j = 1; j <= n; j++){
if(j != i){
int tmp = a[j][i] * inv % MOD;
for(int k = i; k <= n * 2; k++)
a[j][k] = ((a[j][k] - a[i][k] * tmp) % MOD + MOD) % MOD;
}
}
for(int j = 1; j <= n * 2; j++)
a[i][j] = a[i][j] * inv % MOD;
}
for(int i = 1; i <= n; i++){
for(int j = n + 1; j <= 2 * n; j++)
printf("%lld ", a[i][j]);
printf("\n");
}
return 0;
}
参考资料
-
程序员的数学3:线性代数 平冈和幸 掘玄
-
理解矩阵乘法 阮一峰
-
线性代数学习笔记(代数版) 自为风月马前卒
-
线性代数学习笔记(几何版) 自为风月马前卒
-
【官方双语/合集】线性代数的本质 - 系列合集 biliblii 3Blue1Brown
-
P3389 【模板】高斯消元法 皎月半洒花
-
数学(5)——线性代数:行列式 Reywmp
-
《线性代数》学习笔记 Alex_wei
本文来自博客园,作者:Orange_new,转载请注明原文链接:https://www.cnblogs.com/JPGOJCZX/p/18422810


 浙公网安备 33010602011771号
浙公网安备 33010602011771号