数据结构研究之借连通性问题看算法设计

今天我们来看一个比较经典的例子，连通性问题（Connectivity）。通过对这个问题的求解，我们来看看对于一个实际问题在设计算法时候的处理思路。

一：连通性问题。

假如已知一个整数对（pair），每个整数代表某个类型的一个对象，而且将P-Q对解释为P和Q连通，假设连通关系具有传递性。

我们的问题有以下几个：

如果我们属于一个整数对p-q，但是此时p-q已经是连通的，那么这个数据就是冗余的，我们需要剔除这个冗余数据。

二：问题分析

其实对于上面的问题最核心的是如何让程序记住已经获得的连通信息，随时可以检索任意两个数字是否连通。这个问题很有实际意义。

比如说：整数可以代表一个网络中的计算机，对代表可以连通的计算机对。我们就可以判断在计算机p-q之间是否连接。在这种情况下我们可能要处理的点有很多，几万，几百万，甚至上亿。所以需要有一个好的算法。下面给出一个截图，如何判断在下面这个网络中，两个点是否连通。

大型连通图

那么我们的算法将会被设计成如下方式：

1：判断一个新对是否是一个新连接，

2：如果新对是一个新连接，将新对的连接信息记录

3：如果不是一个新连接，忽略新对的信息

那么问题将会被简化为两个小问题：

记录连接对信息，和查找两个点是否连接。

三：算法设计

开发一个有效的算法解决一个已知问题的第一步就是使用一个能解决问题的简单的算法。比如说对于上面的判断连接性问题，最近单最直白的方式，就是将所有的连接对全部记录下来，用一个函数去遍历判断两个点是否连通。

上面这个简单的算法可以解决问题，但是他也有他的瓶颈，现实中可能数据量非常大，不可能保存每个连接对，更加重要的是，没有简单的方法根据连接对判断两个点的连通性。所有我们需要解决以上两个问题。

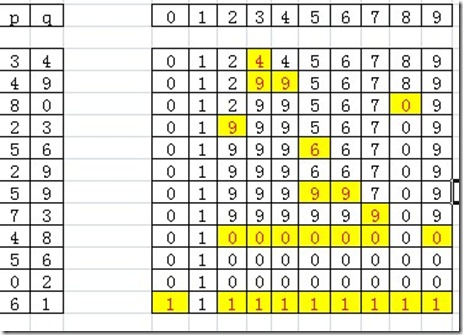
对于连接对太多的情况，我们不去使用连接对来保存，而是使用一个数组来表示所有的点A[n],为了区分所有的元素，我们设置A[i]=i,(0<=i<n).当我们得到一个连接对，我们就将这个连接对的所有值都设置为相同。如果我们得到P-Q，我们就设置所有等于P的元素的值全部改为Q。这样的话所有连通的元素值将会相同。

四：编码过程

/// <summary>
    /// 一个存储连通性信息的类
    /// </summary>
    class ConnectivitySet
    {
        //定义节点个数
        private const int N = 10000;
        private int[] id;
        public ConnectivitySet()
        {
            //存储n个节点
            id = new int[N];
            for (int i = 0; i < N;i++ )
            {
                id[i] = i;
            }
        }

        public void AddPair(int p,int q)
        {
            if (p<0||p>N||q<0||q>N)
            {
                Console.WriteLine("input error!p={0},q={1}.",p,q);
            }
            if (p!=q&&id[p]!=id[q])
            {//如果p-q连通,设置所有和id[p]相连通的节点值都为id[q]
                int t = id[p];
                for (int i = 0; i < N;i++ )
                {
                    if (id[i]==t)
                    {
                        id[i] = id[q];
                    }
                }
            }
        }

        public bool IsConnectivity(int p,int q)
        {
            if (p < 0 || p > N || q < 0 || q > N)
            {
                Console.WriteLine("input error!p={0},q={1}.", p, q);
                return false;
            }
            //判断两个节点是否连通
            return id[p] == id[q];
        }
    }

上面的代码实现了我们的想法，对于新加入的连接对，我们把他们记录到数组中，为了实现查找，我们只需要测试两个节点的值是否一致，当然他的设置过程包括扫描整个数组找出连通的节点并设置新值。

所以说上面的算法是一个快速查找慢速并集的算法。

五：算法的效率评估

如果有N的对象，M个有效连通对的话，我们的并集运算将会进行M*N次。对于现代计算机系统可能有几百万个对象，几亿个连接对，所以上面这种算法在实际应用中是不可行的，那么我们将如何应对呢？

六：算法优化

1：我们下来考虑一个与我们上面算法互补的一个算法，快速并集。

他也是基于相同的数据结构---根据对象索引数组，但是它使用了不同的值来解释，导致了更加复杂的抽象结构。

如图所示，集合中的节点在一个没有环路的集合中，每个对象指向该集合中的另一个节点，如果当前的节点仅仅指向自己本身，那么他就是一个连通链的顶节点。

如果有一个连通数对（p-q），那么我们分别找出P的顶节点和Q的顶节点，如果两个顶节点相同，表示p-q已经连通了。如果不相同我们设置其中一个顶节点指向另一个。

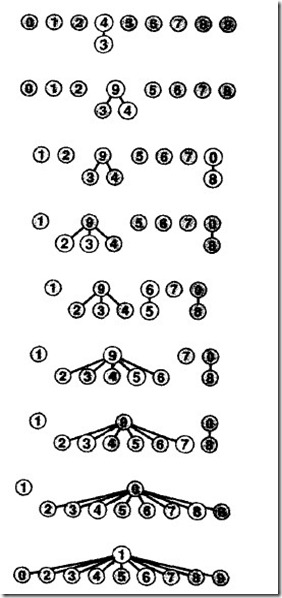
看上去添加连通性的过程是类似于如下这个方式：

代码实现如下：

class ConnectivityTreeSet
    {
         //定义节点个数
        private const int N = 10000;
        private int[] id;
        public ConnectivityTreeSet()
        {
            //存储n个节点
            id = new int[N];
            for (int i = 0; i < N;i++ )
            {
                id[i] = i;
            }
        }
        public void AddPair(int p, int q)
        {
            if (p < 0 || p > N || q < 0 || q > N)
            {
                Console.WriteLine("input error!p={0},q={1}.", p, q);
            }
            //找到P的顶节点
            while (id[p]!=p)
            {
                p = id[p];
            }
            //找到Q的顶节点
            while (id[q] != q)
            {
                q = id[q];
            }
            //如果两个节点不连通
            if (p!=q)
            {//设置连通
                id[p] = q;
            }
        }

        public bool IsConnectivity(int p, int q)
        {
            if (p < 0 || p > N || q < 0 || q > N)
            {
                Console.WriteLine("input error!p={0},q={1}.", p, q);
                return false;
            }
            //判断两个节点是否连通
            //找到P的顶节点
            while (id[p] != p)
            {
                p = id[p];
            }
            //找到Q的顶节点
            while (id[q] != q)
            {
                q = id[q];
            }
            return p == q;
        }
    }

其实我们实现的这个数据结构叫做树，我们会在以后的学习中慢慢的去了解这个数据结构。

2：上面的代码中还是可以优化，因为我们在寻找顶节点的时候是通过一个while循环来操作的，可以通过使用for循环来替代，简化代码：

            //找到P的顶节点
            for (; id[p] != p; p = id[p]) 
            //找到Q的顶节点
            for (; id[q] != q; q = id[q])

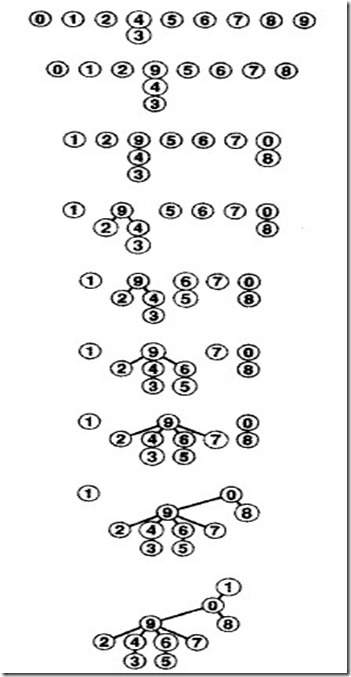
快速并集看起来比我们之前的算法要快一些，因为他不必要在每次插入数对的时候遍历整个数组。如果我们输入的数对满足一下条件（i，i+1），（0<i<N）.那么第一个元素将指向第二个，第二个又指向第三个，如果对于第一个元素做查找运算（查找顶节点），将会进行N-1次遍历，所有对于前面所有的元素来说平均遍历次数为(N-1)/2.说白了就是因为我们再添加数的时候将大树添加为小树的一个节点，导致每个子节点到顶节点的距离变得越来越长。

3：为此我们需要改善一下，在将两个树合并的时候，设置为将小树并到大树上。

那么代码中就必须去记录这个树的最大长度。我们必须借助一个辅助的数组来储存这个信息。在连接两个树的时候选择将小树连接到大树上。

 
public void AddPair(int p, int q)
        {
            if (p < 0 || p > N || q < 0 || q > N)
            {
                Console.WriteLine("input error!p={0},q={1}.", p, q);
            }
            //找到P的顶节点
            for (; id[p] != p; p = id[p]) 
            //找到Q的顶节点
            for (; id[q] != q; q = id[q])
            //如果两个节点不连通
            if (p!=q)
            {//设置连通
                if (size[p]<size[q])
                {
                    id[p] = q;
                    size[q] += size[p];
                }
                else
                {
                    id[q] = p;
                    size[p] += size[q];
                }
            }
        }





        {
            if (p < 0 || p > N || q < 0 || q > N)
            {
                Console.WriteLine("input error!p={0},q={1}.", p, q);
            }
            //找到P的顶节点
            for (; id[p] != p; p = id[p]) 
            //找到Q的顶节点
            for (; id[q] != q; q = id[q])
            //如果两个节点不连通
            if (p!=q)
            {//设置连通
                if (size[p]<size[q])
                {
                    id[p] = q;
                    size[q] += size[p];
                }
                else
                {
                    id[q] = p;
                    size[p] += size[q];
                }
            }
        }

加权连接的方式最坏的情况是，每次两个树进行连接的时候，树的大小都是相同的。如果对象的个数小于2^n个，那么从节点到顶节点的最大距离就是n-1.
这样大大提高了我们连通树中查找某个节点顶节点的效率。

4：当然对于我们的应用程序来说，我们最希望的结果是每个节点都指向新的根，这样我们的搜索效率会大大提高。虽然我们不可能做到每个节点都指向根，但是我们有一些简单有效的方法来压缩整个树，使树的高度大大减小。比如说如果一个树中的结构超过了3层，我们就可以压缩一下：

1--》2---》3可以压缩成1---》3《----2.

我们在遍历一个树找顶节点的同时，可以将当前树压缩一下：

 public void AddPair(int p, int q)
        {
            if (p < 0 || p > N || q < 0 || q > N)
            {
                Console.WriteLine("input error!p={0},q={1}.", p, q);
            }
            //找到P的顶节点
            for (; id[p] != p; p = id[p])
            {//让当前节点指向他父节点的父节点，压缩树
                id[p] = id[id[p]];
            }
            //找到Q的顶节点
            for (; id[q] != q; q = id[q])
            {//让当前节点指向他父节点的父节点，压缩树
                id[1] = id[id[q]];
            }
            //如果两个节点不连通
            if (p!=q)
            {//设置连通
                if (size[p]<size[q])
                {
                    id[p] = q;
                    size[q] += size[p];
                }
                else
                {
                    id[q] = p;
                    size[p] += size[q];
                }
            }
        }

下面我们看一个例子：

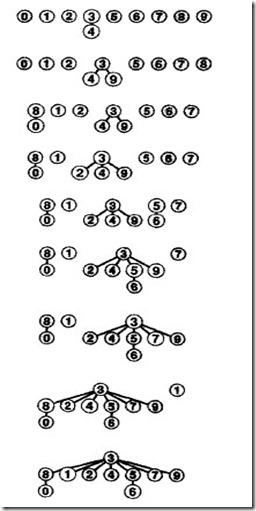
对于我们寻找8的顶节点的时候同时进行压缩，等找到顶节点后，树的结构也由上面的形式变成了下面的格式。

这样大大的减少了任意一个节点到顶节点的距离，在寻找的时候遍历的次数大大减少。

现在这个算法已经是一个比较优良的算法，兼顾了并集时的运行速度以及查找时候的运行速度，所以说这个算法已经基本可以满足我们的实际问题的解决。

六：总结

回过头看我们这个问题解决过程中，对于算法的一步一步的改进，每一步的改进都是对算法的优化，总结一下我们算法设计的过程。

我们开发的过程是这样的：

1：确定问题的本质，确定基本的抽象运算。

2：对简单算法先仔细的开发出一个实现。

3：通过逐级的细化，以便能够得到优化，通过实验分析或者数学分析来验证和改进构思。

4：找出算法中高级的抽象表示，或者具有改进版本的核心改动的算法。

5：在可能的情况下，尽量争取最坏情况的性能保证，但是同时呢还要保证普通情况下的性能。