数据结构之单链表二

上一篇文章中我们讨论了链表的一些基本的操作，这一篇我们来看看一些比较特殊的操作。

先看第一个问题：

一：相交链表

顾名思义，相交链表，就以为着两个链表之间有交点，对于单链表来说，两个链表从交点开始，他们的元素都是相同的。

 

例如：

 

1--->2—>3--->4\

                               \

                                 10—>11—>12—>13

                               /

7—>8—>9—>5 /

第一个问题随之到来，如何判断两个链表是否相交？

方法一：将链表2接在链表1的结尾, 如果从链表2的表头开始遍历 最终到达链表2的表头 说明两个链表相交.

1--->2—>3--->4\

                               \

                                 10—>11—>12—>13

                               /                                         |

7—>8—>9—>5 /                                   |

个-----------------------------<-----------------  |

如果两个链表不想交，那么5--->10之间无联系，遍历到5就该停止，如果连接，那么就会遍历至13，由于13的下一个节点指向链表2个表头也就是7，那么只要检查我们从7能够回到7，就证明两个链表相交。

static bool JudgeIntersectLink1(Link head1,Link head2)
        {
            Link t1 = head1;
            while (t1.Next != null)
            {
                t1 = t1.Next;
            }
            t1.Next = head2;
            Link t = head2;
            while (t.Next!=null)
            {
                t = t.Next;
                if (t == head2)
                {
                    t1.Next = null;
                    return true;
                }
            }
            t1.Next = null;
            return false;
        }

方法二：方法二特别简单，如果两个链表相交，那么他们最后一个元素必定相同。

static bool JudgeIntersectLink2(Link head1,Link head2)
        {
            Link t1 = head1;
            Link t2 = head2;
            while (t1.Next !=null)
            {
                t1 = t1.Next;
            }
            while (t2.Next != null)
            {
                t2 = t2.Next;
            }
            return t1 == t2;
        }

下来来看第二个问题，既然相交那么能否找到交点？

其实也很简单，如果两个链表长度相同，我们设置两个指针，同时从两个表头遍历，如果两个指针指向的元素相同，那么这两个指针所指的元素就是相交点。但是事实上所有的链表长度几乎都不相同，那么我们需要将指针调整好，设第一个链表的长度为M,第二个链表的长度为N，（M>N）那么我们想让第一个链表的指针移动M-N步。然后再进行遍历。

public static Link GetIntersect(Link head1, Link head2)
        {
            int M = 0, N = 0;
            Link t1 = head1;
            Link t2 = head2;
            while (t1.Next != null)
            {
                t1 = t1.Next;
                M++;
            }
            while (t2.Next != null)
            {
                t2 = t2.Next;
                N++;
            }
            //如果 末尾一个元素不同 则必定不想交
            if (t1 != t2)
            {
                return null;
            }
            t1 = head1;
            t2 = head2;
            if (M>N)
            {
                for (int i = 0; i < M - N;i++ )
                {
                    t1 = t1.Next;
                }
            }
            else if (N>M)
            {
                for (int i = 0; i <N - M; i++)
                {
                    t2 = t2.Next;
                }
            }

            while (true)
            {
                if (t1 == t2)
                {
                    return t1;
                }
                t1 = t1.Next;
                t2 = t2.Next;
            }
        }

二：链表的环

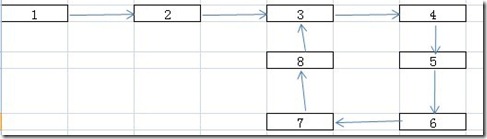
链表中有两个元素的next指针，指向当前链表中的同一个元素，这样就在链表中形成了一个环。

根据我们对链表中环的理解，我们可以理解成下图：

那么如果一个链表中有环，我们遍历将会无限的运行下去，这样我们在处理的时候就会陷入死循环，所以判断一个链表是否有环是非常有必要的。

判断一个链表是否有环：

最常用的判断一个链表有环的方式就是设置两个指针，point1每次移动一个节点，而指针point2每次移动两个节点，如果链表中无环，那么point2会首先遍历完成，永远不会和point1重合。如果有环，则point2和point1总会重合。

        /// <summary>
        /// 判断一个链表是否有环
        /// </summary>
        /// <param name="t"></param>
        /// <returns></returns>
        static bool JudgeCircleExists(Link head)
        {
            Link first = head;  //1 step each time
            Link second = head; //2 steps each time
            while (second.Next != null && second.Next.Next != null)
            {
                second = second.Next.Next;
                first = first.Next;
                if (second == first)
                    return true;
            }
            return false;
        }

那位筒子有其他的处理方式？？

判断环的长度：

上面我们判断一个链表是否有环，那么我们能否找出环的长度呢？

其实很简单，沿着我们环中的任意一点开始遍历，一旦再次回到我们遍历的起始点，就获得了环的长度。

         /// <summary>
        /// 如果有环输出环的长度
        /// </summary>
        /// <param name="point"></param>
        /// <returns></returns>
        static int GetCircleLength(Link point)
        {
            int length = 1;
            Link curr = point;
            while (curr.Next != point)
            {
                length++;
                curr = curr.Next;
            }
            return length;
        }

判断链表中环的起始点：

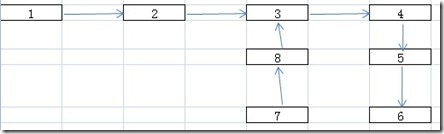
如果我们将我们有环的链表从我们判断是否有环的哪个过程中的结束点（两个指针的重合点）将这个环拆开，那么这个链表将变成两个相交的链表。

链表1为1,2,3,4,5,6.

链表2为7,8,3.

这两个链表的相交点3就是原来哪个有环链表的环起始点。所以判断一个有环链表的环起始点转化成了判断两个链表的相交点。

        /// <summary>
        /// 如果有环 输出环的起始点
        /// 如果从检验环的终结点切割 将一个有环链表转化为两个相交链表
        /// 那么相交点就是环的起始点
        /// </summary>
        /// <param name="head">链表头</param>
        /// <param name="point">环的检测终结点</param>
        /// <returns></returns>
        static Link GetCircleStart(Link head,Link point)
        {
            int M = 0, N = 0;
            Link t1 = head;
            Link t2 = point;
            while (t1.Next != point)
            {
                t1 = t1.Next;
                M++;
            }
            while (t2.Next != point)
            {
                t2 = t2.Next;
                N++;
            }
            t1 = head;
            t2 = point;
            if (M > N)
            {
                for (int i = 0; i < M - N; i++)
                {
                    t1 = t1.Next;
                }
            }
            else if (N > M)
            {
                for (int i = 0; i < N - M; i++)
                {
                    t2 = t2.Next;
                }
            }

            while (true)
            {
                if (t1 == t2)
                {
                    return t1;
                }
                t1 = t1.Next;
                t2 = t2.Next;
            }
        }

以上就是对于链表中一些特殊问题的处理。