优化算法：LevenbergMarquardt
目录
1 高斯牛顿法
高斯牛顿法是线性搜索与信赖阈搜索的优化方法基础，它将损失函数进行一阶展开：
\[f(x + \bigtriangleup x) \approx {f(x) + J(x) \bigtriangleup x}
\]
这里\(J(x)\)实际为\(m\times{n}\)矩阵，\(f(x)\)为一个参数函数\(r_ᵢ(x) = yᵢ - M(x)\)
1.1 目的
寻找\(\bigtriangleup x\)使得\(||f(x+\bigtriangleup x)||^2\)最小化，即转换为优化问题：
\[\bigtriangleup \hat{x}=arg \min_{\bigtriangleup x} \frac{1}{2} ||{f(x) + J(x) \bigtriangleup x}||^2
\]
1.2 步骤
设\(F(x)=\frac{1}{2}||f(x) + J(x)\bigtriangleup x||^2\)
\[F(x)=(f(x) + J(x)\bigtriangleup x)^T(f(x) + J(x) \bigtriangleup x)\\
= (f^T(x) + \bigtriangleup^Tx J^T(x))(f(x) + J(x) \bigtriangleup x)\\
= f^T(x) f(x) + f^T(x) J(x)\bigtriangleup x + \bigtriangleup ^TxJ^T(x) f(x) + \bigtriangleup ^Tx J^T(x)J(x) \bigtriangleup x\\
= f^2(x) + f^T(x)J(x)\bigtriangleup x + \bigtriangleup ^Tx J^T(x)J(x) \bigtriangleup x \\
= f^2(x) + 2f^T(x)J(x) \bigtriangleup x + \bigtriangleup ^Tx J^T(x)J(x) \bigtriangleup x
\]
这里解释下：
\[f(x)\in R^{n\times 1}\\
f(x)为残差，例如(y-y')^2\\
x\in R^{n \times 1} \\
f^T(x)J(x)\bigtriangleup x为标量\\
J(x) = \begin{bmatrix}
\frac{\partial r_1}{\partial x_1} & ... & \frac{\partial r_1}{\partial x_n} \\
\vdots & \vdots & \vdots \\
\frac{\partial r_m}{\partial x_1} & ... & \frac{\partial r_m}{\partial x_n} \\
\end{bmatrix}
\]
1.3 最终更新公式
\[\frac{\partial F}{\partial {\bigtriangleup x}} = 2J^T(x)f(x) + 2J^T(x)J(x){\bigtriangleup x}=0\\
J^T(x)J(x){\bigtriangleup x}=-J^T(x)f(x)
\]
2. LM
2.1 整体流程
2.2 算法介绍
- LM算法给增量\(Δx\)添加了一个信赖域，即
\[\min_{Δx}\frac{1}{2}||f(x_k) + J(x_k)Δx_k||^2 ,s.t ||DΔx_K||^2<=\mu
\]
- 拉格朗日乘子法转换为无约束的问题：
\[\min_{Δx}\frac{1}{2}||f(x_k) + J(x_k)Δx_k||^2 +\lambda/2||DΔx_K||^2 \\
\Longrightarrow H Δx+\lambda D^TDΔx=g
\]
- LM算法实际求解的是：\[(J^TJ+\lambda diag(J^TJ) \bigtriangleup = J^Tr \]
- 然后：\[x_{new} = x_{prev} - \bigtriangleup \]
- 注意
- 用的是 diag *= (1+λ)，不是 + λI；前者是椭圆的球形信赖域，后者为球形
- 解的是 masked 子空间
- 默认 SVD
2.3 opencv的实现流程
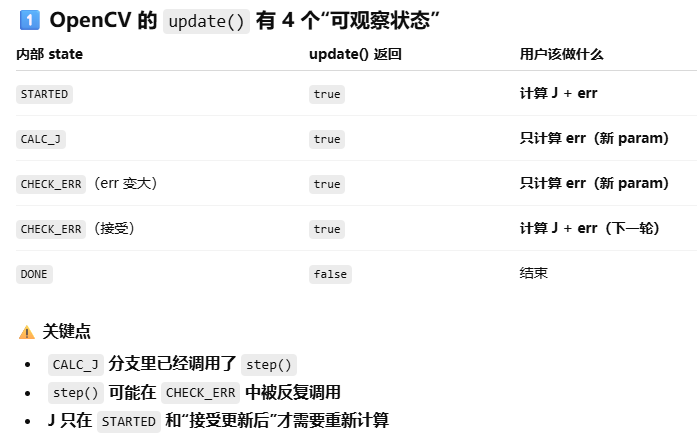
STARTED
└─ 返回 param + J + err（算 J）
CALC_J
├─ JtJ, JtErr
├─ prevParam = param
├─ step() 计算(J^T*J + λ*I) * Δx = -J^T*e中的Δx，并更新到状态变量x_
└─ 返回 param + err（算 err）
CHECK_ERR
├─ if err > prevErr
│ ├─ lambda++
│ ├─ step()
│ └─ 返回 param + err
└─ else（接受）
├─ lambda--
├─ 收敛判断
└─ 返回 param + J + err
3 实现
3.1 opencv实现
class CV_EXPORTS CvLevMarq
{
public:
CvLevMarq();
CvLevMarq( int nparams, int nerrs, CvTermCriteria criteria=
cvTermCriteria(CV_TERMCRIT_EPS+CV_TERMCRIT_ITER,30,DBL_EPSILON),
bool completeSymmFlag=false );
~CvLevMarq();
/*
* 功能：
* 参数：
* [in] nparams 优化变量的参数
* [in] nerrs nerrs代表样本的个数（一个测量点代表两个样本x和y）。
nerrs = 0，优化时使用updateAlt函数，因为此函数不关心样本个数（JtJ外部计算，自然不需要知道J的大小）
nerrs > 0，优化时使用update函数，应为内部需要使用J的大小，所以J的维度需要提前声明，其维度大小为nerrs*nparams
* [in] criteria 迭代停止标准
* [in] completeSymmFlag 当nerrs=0时有效。防止外部计算得到的JtJ不对称。此标记位不管是false和true都会使JtJ 变为对称。
*
* 返回值：
*
* 备注：
* 此函数相对于updateAlt函数，计算相对简单，但自己自由发挥的空间较少。例如代权重的最小二乘此函数就无法实现。
*
*/
void init( int nparams, int nerrs, CvTermCriteria criteria=
cvTermCriteria(CV_TERMCRIT_EPS+CV_TERMCRIT_ITER,30,DBL_EPSILON),
bool completeSymmFlag=false );
/*
* 功能：
* 参数：
* [out] param 需要优化的参数，根据内部参数的优化状况，对当前参数进行输出，方便外部误差的计算
* [in] J 目标函数的偏导数，内部计算JtJ
* [in] err 内部计算JtErr 和 errNorm
*
* 返回值：
*
* 备注：
* 此函数相对于updateAlt函数，计算相对简单，但自己自由发挥的空间较少。例如代权重的最小二乘此函数就无法实现。
*
*/
bool update( const CvMat*& param, CvMat*& J, CvMat*& err );
/*
* 功能：
* 参数：
* [out] param 需要优化的参数，根据内部参数的优化状况，对当前参数进行输出，方便外部误差的计算
* [in] JtJ 正规方程左侧的部分，此变量与类内部成员变量关联，在此函数后面对其赋值。可以变成J'ΩJ
* [in] JtErr 正规方程右侧的部分，此变量与类内部成员变量关联，在此函数后面对其赋值。
* [in] errNorm 测量误差（测量值减去计算出的测量值的模），此变量与类内部成员变量关联，在此函数后面对其赋值。
*
* 返回值：
*
* 备注：
* 目标函数的导数，正规方程的左侧和右侧计算都是在外部完成计算的，测量误差的计算也是在外部完成的。
*/
bool updateAlt( const CvMat*& param, CvMat*& JtJ, CvMat*& JtErr, double*& errNorm ); // 控制优化过程中的逻辑步骤（DONE, STARTED, CALC_J, CHECK_ERR）
void clear();
void step(); // 计算正规方程的解，用SVD计算
enum { DONE=0, STARTED=1, CALC_J=2, CHECK_ERR=3 };
cv::Ptr<CvMat> mask; // 标记优化过程中不优化的量。0代表不优化，1代表优化。大小跟param相同
cv::Ptr<CvMat> prevParam; // 前一步的优化参数，用途有两个：1、判断变量是否在变化，不变化停止迭代。2、在此参数上减去一个高斯方向得到下一个参数。
cv::Ptr<CvMat> param; // 所有要优化的变脸集合
cv::Ptr<CvMat> J; // 目标函数的偏导数
cv::Ptr<CvMat> err; // 测量误差向量
cv::Ptr<CvMat> JtJ; // 正规方程左侧的部分
cv::Ptr<CvMat> JtJN; // 去掉非优化变量后的正规方程左侧部分
cv::Ptr<CvMat> JtErr; // 正规方程右侧的部分
cv::Ptr<CvMat> JtJV; // 去掉非优化变量的JtErr，
cv::Ptr<CvMat> JtJW; // 去掉非优化变量后待求向量
double prevErrNorm, errNorm; // 测量误差，更新前的测量误差，更新后的测量误差
int lambdaLg10; // LM 算法中的lanbda，此处的lamdaLg10 加1代表lambda变大10倍，减1缩小10倍
CvTermCriteria criteria;
int state; // 优化步骤中的状态
int iters; // 记录迭代的次数
bool completeSymmFlag; // 使去掉非优化变量后的JtJN变成对称矩阵，只是在updateAlt函数是有用。
int solveMethod; // 正规方程的解法
};
CvLevMarq::CvLevMarq()
{
lambdaLg10 = 0; state = DONE;
criteria = cvTermCriteria(0,0,0);
iters = 0;
completeSymmFlag = false;
errNorm = prevErrNorm = DBL_MAX;
solveMethod = cv::DECOMP_SVD;
}
CvLevMarq::CvLevMarq( int nparams, int nerrs, CvTermCriteria criteria0, bool _completeSymmFlag )
{
init(nparams, nerrs, criteria0, _completeSymmFlag);
}
void CvLevMarq::clear()
{
mask.release();
prevParam.release();
param.release();
J.release();
err.release();
JtJ.release();
JtJN.release();
JtErr.release();
JtJV.release();
JtJW.release();
}
CvLevMarq::~CvLevMarq()
{
clear();
}
void CvLevMarq::init( int nparams, int nerrs, CvTermCriteria criteria0, bool _completeSymmFlag )
{
if( !param || param->rows != nparams || nerrs != (err ? err->rows : 0) )
clear();
mask.reset(cvCreateMat( nparams, 1, CV_8U ));
cvSet(mask, cvScalarAll(1));
prevParam.reset(cvCreateMat( nparams, 1, CV_64F ));
param.reset(cvCreateMat( nparams, 1, CV_64F ));
JtJ.reset(cvCreateMat( nparams, nparams, CV_64F ));
JtErr.reset(cvCreateMat( nparams, 1, CV_64F ));
if( nerrs > 0 )
{
J.reset(cvCreateMat( nerrs, nparams, CV_64F ));
err.reset(cvCreateMat( nerrs, 1, CV_64F ));
}
errNorm = prevErrNorm = DBL_MAX;
lambdaLg10 = -3;
criteria = criteria0;
if( criteria.type & CV_TERMCRIT_ITER )
criteria.max_iter = MIN(MAX(criteria.max_iter,1),1000);
else
criteria.max_iter = 30;
if( criteria.type & CV_TERMCRIT_EPS )
criteria.epsilon = MAX(criteria.epsilon, 0);
else
criteria.epsilon = DBL_EPSILON;
state = STARTED;
iters = 0;
completeSymmFlag = _completeSymmFlag;
solveMethod = cv::DECOMP_SVD;
}
bool CvLevMarq::update( const CvMat*& _param, CvMat*& matJ, CvMat*& _err )
{
matJ = _err = 0;
CV_Assert( !err.empty() );
if( state == DONE )
{
_param = param;
return false;
}
if( state == STARTED )
{
_param = param;
cvZero( J );
cvZero( err );
matJ = J;
_err = err;
state = CALC_J;
return true;
}
if( state == CALC_J )
{
cvMulTransposed( J, JtJ, 1 );
cvGEMM( J, err, 1, 0, 0, JtErr, CV_GEMM_A_T );
cvCopy( param, prevParam );
step();
if( iters == 0 )
prevErrNorm = cvNorm(err, 0, CV_L2);
_param = param;
cvZero( err );
_err = err;
state = CHECK_ERR;
return true;
}
CV_Assert( state == CHECK_ERR );
errNorm = cvNorm( err, 0, CV_L2 );
if( errNorm > prevErrNorm )
{
if( ++lambdaLg10 <= 16 )
{
step();
_param = param;
cvZero( err );
_err = err;
state = CHECK_ERR;
return true;
}
}
lambdaLg10 = MAX(lambdaLg10-1, -16);
if( ++iters >= criteria.max_iter ||
cvNorm(param, prevParam, CV_RELATIVE_L2) < criteria.epsilon )
{
_param = param;
state = DONE;
return true;
}
prevErrNorm = errNorm;
_param = param;
cvZero(J);
matJ = J;
_err = err;
state = CALC_J;
return true;
}
namespace {
static void subMatrix(const cv::Mat& src, cv::Mat& dst, const std::vector<uchar>& cols,
const std::vector<uchar>& rows) {
int nonzeros_cols = cv::countNonZero(cols);
cv::Mat tmp(src.rows, nonzeros_cols, CV_64FC1);
for (int i = 0, j = 0; i < (int)cols.size(); i++)
{
if (cols[i])
{
src.col(i).copyTo(tmp.col(j++));
}
}
int nonzeros_rows = cv::countNonZero(rows);
dst.create(nonzeros_rows, nonzeros_cols, CV_64FC1);
for (int i = 0, j = 0; i < (int)rows.size(); i++)
{
if (rows[i])
{
tmp.row(i).copyTo(dst.row(j++));
}
}
}
}
void CvLevMarq::step()
{
using namespace cv;
const double LOG10 = log(10.);
double lambda = exp(lambdaLg10*LOG10);
int nparams = param->rows;
Mat _JtJ = cvarrToMat(JtJ);
Mat _mask = cvarrToMat(mask);
int nparams_nz = countNonZero(_mask);
if(!JtJN || JtJN->rows != nparams_nz) {
// prevent re-allocation in every step
JtJN.reset(cvCreateMat( nparams_nz, nparams_nz, CV_64F ));
JtJV.reset(cvCreateMat( nparams_nz, 1, CV_64F ));
JtJW.reset(cvCreateMat( nparams_nz, 1, CV_64F ));
}
Mat _JtJN = cvarrToMat(JtJN);
Mat _JtErr = cvarrToMat(JtJV);
Mat_<double> nonzero_param = cvarrToMat(JtJW);
subMatrix(cvarrToMat(JtErr), _JtErr, std::vector<uchar>(1, 1), _mask);
subMatrix(_JtJ, _JtJN, _mask, _mask);
if( !err )
completeSymm( _JtJN, completeSymmFlag );
_JtJN.diag() *= 1. + lambda;
solve(_JtJN, _ΔxJtErr, nonzero_param, solveMethod);
int j = 0;
for( int i = 0; i < nparams; i++ )
param->data.db[i] = prevParam->data.db[i] - (mask->data.ptr[i] ? nonzero_param(j++) : 0);
}
3.2 python 实现
'''
#Implement LM algorithm only using basic python
#Author:Leo Ma
#For csmath2019 assignment4,ZheJiang University
#Date:2019.04.28
'''
import numpy as np
import matplotlib.pyplot as plt
#input data, whose shape is (num_data,1)
#data_input=np.array([[0.25, 0.5, 1, 1.5, 2, 3, 4, 6, 8]]).T
#data_output=np.array([[19.21, 18.15, 15.36, 14.10, 12.89, 9.32, 7.45, 5.24, 3.01]]).T
tao = 10**-3
threshold_stop = 10**-15
threshold_step = 10**-15
threshold_residual = 10**-15
residual_memory = []
#construct a user function
def my_Func(params,input_data):
a = params[0,0]
b = params[1,0]
#c = params[2,0]
#d = params[3,0]
return a*np.exp(b*input_data)
#return a*np.sin(b*input_data[:,0])+c*np.cos(d*input_data[:,1])
#generating the input_data and output_data,whose shape both is (num_data,1)
def generate_data(params,num_data):
x = np.array(np.linspace(0,10,num_data)).reshape(num_data,1) # 产生包含噪声的数据
mid,sigma = 0,5
y = my_Func(params,x) + np.random.normal(mid, sigma, num_data).reshape(num_data,1)
return x,y
#calculating the derive of pointed parameter,whose shape is (num_data,1)
def cal_deriv(params,input_data,param_index):
params1 = params.copy()
params2 = params.copy()
params1[param_index,0] += 0.000001
params2[param_index,0] -= 0.000001
data_est_output1 = my_Func(params1,input_data)
data_est_output2 = my_Func(params2,input_data)
return (data_est_output1 - data_est_output2) / 0.000002
#calculating jacobian matrix,whose shape is (num_data,num_params)
def cal_Jacobian(params,input_data):
num_params = np.shape(params)[0]
num_data = np.shape(input_data)[0]
J = np.zeros((num_data,num_params))
for i in range(0,num_params):
J[:,i] = np.asarray(list(cal_deriv(params,input_data,i))).reshape((100))
return J
#calculating residual, whose shape is (num_data,1)
def cal_residual(params,input_data,output_data):
data_est_output = my_Func(params,input_data)
residual = output_data - data_est_output
return residual
'''
#calculating Hessian matrix, whose shape is (num_params,num_params)
def cal_Hessian_LM(Jacobian,u,num_params):
H = Jacobian.T.dot(Jacobian) + u*np.eye(num_params)
return H
#calculating g, whose shape is (num_params,1)
def cal_g(Jacobian,residual):
g = Jacobian.T.dot(residual)
return g
#calculating s,whose shape is (num_params,1)
def cal_step(Hessian_LM,g):
s = Hessian_LM.I.dot(g)
return s
'''
#get the init u, using equation u=tao*max(Aii)
def get_init_u(A,tao):
m = np.shape(A)[0]
Aii = []
for i in range(0,m):
Aii.append(A[i,i])
u = tao*max(Aii)
return u
#LM algorithm
def LM(num_iter,params,input_data,output_data):
num_params = np.shape(params)[0]#the number of params
k = 0#set the init iter count is 0
#calculating the init residual
residual = cal_residual(params,input_data,output_data)
#calculating the init Jocobian matrix
Jacobian = cal_Jacobian(params,input_data)
A = Jacobian.T.dot(Jacobian)#calculating the init A
g = Jacobian.T.dot(residual)#calculating the init gradient g
stop = (np.linalg.norm(g, ord=np.inf) <= threshold_stop)#set the init stop
u = get_init_u(A,tao)#set the init u
v = 2#set the init v=2
while((not stop) and (k<num_iter)):
k+=1
while(1):
Hessian_LM = A + u*np.eye(num_params)#calculating Hessian matrix in LM
step = np.linalg.inv(Hessian_LM).dot(g)#calculating the update step
if(np.linalg.norm(step) <= threshold_step):
stop = True
else:
new_params = params + step#update params using step
new_residual = cal_residual(new_params,input_data,output_data)#get new residual using new params
rou = (np.linalg.norm(residual)**2 - np.linalg.norm(new_residual)**2) / (step.T.dot(u*step+g))
if rou > 0:
params = new_params
residual = new_residual
residual_memory.append(np.linalg.norm(residual)**2)
#print (np.linalg.norm(new_residual)**2)
Jacobian = cal_Jacobian(params,input_data)#recalculating Jacobian matrix with new params
A = Jacobian.T.dot(Jacobian)#recalculating A
g = Jacobian.T.dot(residual)#recalculating gradient g
stop = (np.linalg.norm(g, ord=np.inf) <= threshold_stop) or (np.linalg.norm(residual)**2 <= threshold_residual)
u = u*max(1/3,1-(2*rou-1)**3)
v = 2
else:
u = u*v
v = 2*v
if(rou > 0 or stop):
break;
return params
def main():
#set the true params for generate_data() function
params = np.zeros((2,1))
params[0,0]=10.0
params[1,0]=0.8
num_data = 100# set the data number
data_input,data_output = generate_data(params,num_data)#generate data as requested
#set the init params for LM algorithm
params[0,0]=6.0
params[1,0]=0.3
#using LM algorithm estimate params
num_iter=100 # the number of iteration
est_params = LM(num_iter,params,data_input,data_output)
print(est_params)
a_est=est_params[0,0]
b_est=est_params[1,0]
#画个图看看状况
plt.scatter(data_input, data_output, color='b')
x = np.arange(0, 100) * 0.1 #生成0-10的共100个数据，然后设置间距为0.1
plt.plot(x,a_est*np.exp(b_est*x),'r',lw=1.0)
plt.xlabel("2018.06.13")
plt.savefig("result_LM.png")
plt.show()
plt.plot(residual_memory)
plt.xlabel("2018.06.13")
plt.savefig("error-iter.png")
plt.show()
if __name__ == '__main__':
main()
3.3 基于eigen实现
/**
* This file is part of LevenbergMarquardt Solver.
*
* Copyright (C) 2018-2020 Dongsheng Yang <ydsf16@buaa.edu.cn> (Beihang University)
* For more information see <https://github.com/ydsf16/LevenbergMarquardt>
*
* LevenbergMarquardt is free software: you can redistribute it and/or modify
* it under the terms of the GNU General Public License as published by
* the Free Software Foundation, either version 3 of the License, or
* (at your option) any later version.
*
* LevenbergMarquardt is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
*
* You should have received a copy of the GNU General Public License
* along with LevenbergMarquardt. If not, see <http://www.gnu.org/licenses/>.
*/
#include <iostream>
#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <opencv2/opencv.hpp>
#include <eigen3/Eigen/Cholesky>
#include <chrono>
/* 计时类 */
class Runtimer{
public:
inline void start()
{
t_s_ = std::chrono::steady_clock::now();
}
inline void stop()
{
t_e_ = std::chrono::steady_clock::now();
}
inline double duration()
{
return std::chrono::duration_cast<std::chrono::duration<double>>(t_e_ - t_s_).count() * 1000.0;
}
private:
std::chrono::steady_clock::time_point t_s_; //start time ponit
std::chrono::steady_clock::time_point t_e_; //stop time point
};
/* 优化方程 */
class LevenbergMarquardt{
public:
LevenbergMarquardt(double* a, double* b, double* c):
a_(a), b_(b), c_(c)
{
epsilon_1_ = 1e-6;
epsilon_2_ = 1e-6;
max_iter_ = 50;
is_out_ = true;
}
void setParameters(double epsilon_1, double epsilon_2, int max_iter, bool is_out)
{
epsilon_1_ = epsilon_1;
epsilon_2_ = epsilon_2;
max_iter_ = max_iter;
is_out_ = is_out;
}
void addObservation(const double& x, const double& y)
{
obs_.push_back(Eigen::Vector2d(x, y));
}
void calcJ_fx()
{
J_ .resize(obs_.size(), 3);
fx_.resize(obs_.size(), 1);
for ( size_t i = 0; i < obs_.size(); i ++)
{
const Eigen::Vector2d& ob = obs_.at(i);
const double& x = ob(0);
const double& y = ob(1);
double j1 = -x*x*exp(*a_ * x*x + *b_*x + *c_);
double j2 = -x*exp(*a_ * x*x + *b_*x + *c_);
double j3 = -exp(*a_ * x*x + *b_*x + *c_);
J_(i, 0 ) = j1;
J_(i, 1) = j2;
J_(i, 2) = j3;
fx_(i, 0) = y - exp( *a_ *x*x + *b_*x +*c_);
}
}
void calcH_g()
{
H_ = J_.transpose() * J_;
g_ = -J_.transpose() * fx_;
}
double getCost()
{
Eigen::MatrixXd cost= fx_.transpose() * fx_;
return cost(0,0);
}
double F(double a, double b, double c)
{
Eigen::MatrixXd fx;
fx.resize(obs_.size(), 1);
for ( size_t i = 0; i < obs_.size(); i ++)
{
const Eigen::Vector2d& ob = obs_.at(i);
const double& x = ob(0);
const double& y = ob(1);
fx(i, 0) = y - exp( a *x*x + b*x +c);
}
Eigen::MatrixXd F = 0.5 * fx.transpose() * fx;
return F(0,0);
}
double L0_L( Eigen::Vector3d& h)
{
Eigen::MatrixXd L = -h.transpose() * J_.transpose() * fx_ - 0.5 * h.transpose() * J_.transpose() * J_ * h;
return L(0,0);
}
void solve()
{
int k = 0;
double nu = 2.0;
calcJ_fx();
calcH_g();
bool found = ( g_.lpNorm<Eigen::Infinity>() < epsilon_1_ );
std::vector<double> A;
A.push_back( H_(0, 0) );
A.push_back( H_(1, 1) );
A.push_back( H_(2,2) );
auto max_p = std::max_element(A.begin(), A.end());
double mu = *max_p;
double sumt =0;
while ( !found && k < max_iter_)
{
Runtimer t;
t.start();
k = k +1;
Eigen::Matrix3d G = H_ + mu * Eigen::Matrix3d::Identity();
Eigen::Vector3d h = G.ldlt().solve(g_);
if( h.norm() <= epsilon_2_ * ( sqrt(*a_**a_ + *b_**b_ + *c_**c_ ) +epsilon_2_ ) )
found = true;
else
{
double na = *a_ + h(0);
double nb = *b_ + h(1);
double nc = *c_ + h(2);
double rho =( F(*a_, *b_, *c_) - F(na, nb, nc) ) / L0_L(h);
if( rho > 0)
{
*a_ = na;
*b_ = nb;
*c_ = nc;
calcJ_fx();
calcH_g();
found = ( g_.lpNorm<Eigen::Infinity>() < epsilon_1_ );
mu = mu * std::max<double>(0.33, 1 - std::pow(2*rho -1, 3));
nu = 2.0;
}
else
{
mu = mu * nu;
nu = 2*nu;
}// if rho > 0
}// if step is too small
t.stop();
if( is_out_ )
{
std::cout << "Iter: " << std::left <<std::setw(3) << k << " Result: "<< std::left <<std::setw(10) << *a_ << " " << std::left <<std::setw(10) << *b_ << " " << std::left <<std::setw(10) << *c_ <<
" step: " << std::left <<std::setw(14) << h.norm() << " cost: "<< std::left <<std::setw(14) << getCost() << " time: " << std::left <<std::setw(14) << t.duration() <<
" total_time: "<< std::left <<std::setw(14) << (sumt += t.duration()) << std::endl;
}
} // while
if( found == true)
std::cout << "\nConverged\n\n";
else
std::cout << "\nDiverged\n\n";
}//function
Eigen::MatrixXd fx_;
Eigen::MatrixXd J_; // 雅克比矩阵
Eigen::Matrix3d H_; // H矩阵
Eigen::Vector3d g_;
std::vector< Eigen::Vector2d> obs_; // 观测
/* 要求的三个参数 */
double* a_, *b_, *c_;
/* parameters */
double epsilon_1_, epsilon_2_;
int max_iter_;
bool is_out_;
};//class LevenbergMarquardt
int main(int argc, char **argv) {
const double aa = 0.1, bb = 0.5, cc = 2; // 实际方程的参数
double a =0.0, b=0.0, c=0.0; // 初值
/* 构造问题 */
LevenbergMarquardt lm(&a, &b, &c);
lm.setParameters(1e-10, 1e-10, 100, true);
/* 制造数据 */
const size_t N = 100; //数据个数
cv::RNG rng(cv::getTickCount());
for( size_t i = 0; i < N; i ++)
{
/* 生产带有高斯噪声的数据 */
double x = rng.uniform(0.0, 1.0) ;
double y = exp(aa*x*x + bb*x + cc) + rng.gaussian(0.05);
/* 添加到观测中 */
lm.addObservation(x, y);
}
/* 用LM法求解 */
lm.solve();
return 0;
}
浙公网安备 33010602011771号